4.2 全反射 同步训练题(Word版含答案)
文档属性
| 名称 | 4.2 全反射 同步训练题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 849.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-03-25 22:33:12 | ||
图片预览




文档简介
4.2全反射 精选训练题
一、选择题
1.已知介质对某单色光的临界角为C,则不正确的是( )
A.该介质对单色光的折射率等于
B.此单色光在该介质中的传播速度等于csinC(c是光在真空中的传播速度)
C.此单色光在该介质中的传播波长是在真空中波长的sinC倍
D.此单色光在该介质中的频率是在真空中的倍
2.光线由某种媒质射向与空气的分界面,当入射角大于450时折射光线消失,由此可断定这种媒质的折射率是( )
A. B. C. D.n=2
3.公路交通标志牌是由基板和附着在基板上的反光膜组成,反光膜一般由镀在玻璃微珠上的铝层组成,夜间能将汽车射来的灯光反射回去,使司机看清交通标志.交通标志牌的结构示意图如图,这种交通标志牌的原理是( )
A.利用了光的反射
B.利用了光的折射
C.利用了光的色散
D.利用了光的全反射
4.一束光从某介质进入真空,方向如图所示,则下列判断中正确的是( )
A.该介质的折射率是
B.该介质的折射率是
C.该介质相对真空发生全反射的临界角是45°
D.光线从介质射入真空的过程中,无论怎样改变入射方向都不可能发生全反射现象
5.自行车上的红色尾灯不仅是装饰品,也是夜间骑车的安全指示灯,它能把来自后面的光照反射回去,某种自行车尾灯可简化为由许多整齐排列的等腰直角棱镜(折射率n>)组成,棱镜的横截面如图所示,一平行于横截面的光线从O点垂直AB边射入棱镜,先后经过AC和CB边反射后,从AB边的O′点射出,则出射光线是( )
A.平行于AC边的光线① B.平行于入射光线的光线②
C.平行于CB边的光线③ D.沿AB边的光线④
6.空气中两条光线a和b从方框左侧入射,分别从方框下方和上方射出,其框外光线如图所示。方框内有两个折射率n=1.5的玻璃全反射棱镜。下列选项中给出了两棱镜四种放置方式的示意图,其中能产生上述效果的是 ( )
A. B. C. D.
7.如图所示,一块上、下表面平行的玻璃砖的厚度为L,玻璃砖的折射率n=,若光从上表面AB射入的入射角i=60°,光在真空中的光速为c,则( )
A.折射角r=30°
B.光在玻璃中传播的时间为
C.光在玻璃中传播的时间为
D.改变入射角i,光在下表面CD可能发生全发射
8.“半潜艇”船体主要部分浸入水中,甲板始终浮出水面,潜艇内的乘客处在海平面以下,可以通过玻璃窗观察水中景物(如图1),原理图2,已知该处海水的折射率为,潜艇玻璃表面和水面垂直,且玻璃的厚度可以忽略,则以下说法中不正确的是( )
A.游客在潜艇内部看到正前方的鱼比实际位置要远一些
B.潜艇正前方的鱼看到潜艇中的人比实际位置要远一些
C.水面上方射入水中的光线不能照射到潜艇内部
D.潜艇内游客用手电筒朝水中照射时,水面上的人不可能看到手电筒发出的光
9.在完全透明的水下某深处,放一点光源,在水面上可见到一个圆形的透光圆面,若透光圆面的半径匀速增大,则光源正( )
A.加速上长 B.加速下降 C.匀速上升 D.匀速下降
10.2009年诺贝尔物理学奖授予英国华裔物理学家高锟,以表彰他在光纤通信研究中的突出贡献.光纤通信是利用了光的全反射的原理,光导纤维由内芯和外套两层组成.下列有关光导纤维的说法中正确的是( )
A.内芯的折射率比外套大,光传播时在内芯与外套的界面发生全反射
B.内芯的折射率比外套小,光传播时在内芯与外套的界面发生全反射
C.内芯的折射率比外套小,光传播时在内芯与外套的界面发生折射
D.内芯的折射率与外套相同,外套的材料有韧性,可以对内芯起保护作用
11.下列说法正确的是( )
A.因为水的密度大于酒精的密度,所以水是光密介质
B.因为水的折射率小于酒精的折射率,所以水对酒精来说是光疏介质
C.同一束光在光密介质中的传播速度较大
D.同一束光在光密介质中的传播速度较小
12.如图是在四川景区九寨沟拍摄的一张风景照片,湖水清澈见底,近处湖面水下的树枝和池底都看得很清楚,而远处则只看到对岸山峰和绿树的倒影,水面下的景物则根本看不到.下列说法中正确的是( )
A.远处山峰的倒影非常清晰,是因为来自山峰的光线在水面上发生了全反射
B.光从空气射入水中,光的波速变小,波长变小
C.远处水面下景物的光线到水面处,入射角较大,可能发生了全反射,所以看不见
D.来自近处水面下景物的光射到水面处,入射角较小,反射光强而折射光弱,因此有较多的能量射出水面而进入人的眼睛中
13.某大学研制出了正六棱柱“隐形衣”,有同学将正六棱柱放进装满水的透明鱼缸,向着棱的方向看,可以看到鱼缸另一侧大学的校徽;用一支铅笔穿过正六棱柱中心轴线的孔洞,再向棱方向观察,铅笔插进孔洞的那段消失不见了(如图甲所示,图乙为光路说明图),关于此实验说法正确的是( )
A.隐形的原理是光发生了全反射
B.光由水进入该介质,折射角大于入射角
C.隐形的原理是光被玻璃吸收了
D.光在该介质中的传播的速度大于在水中传播速度
二、填空题
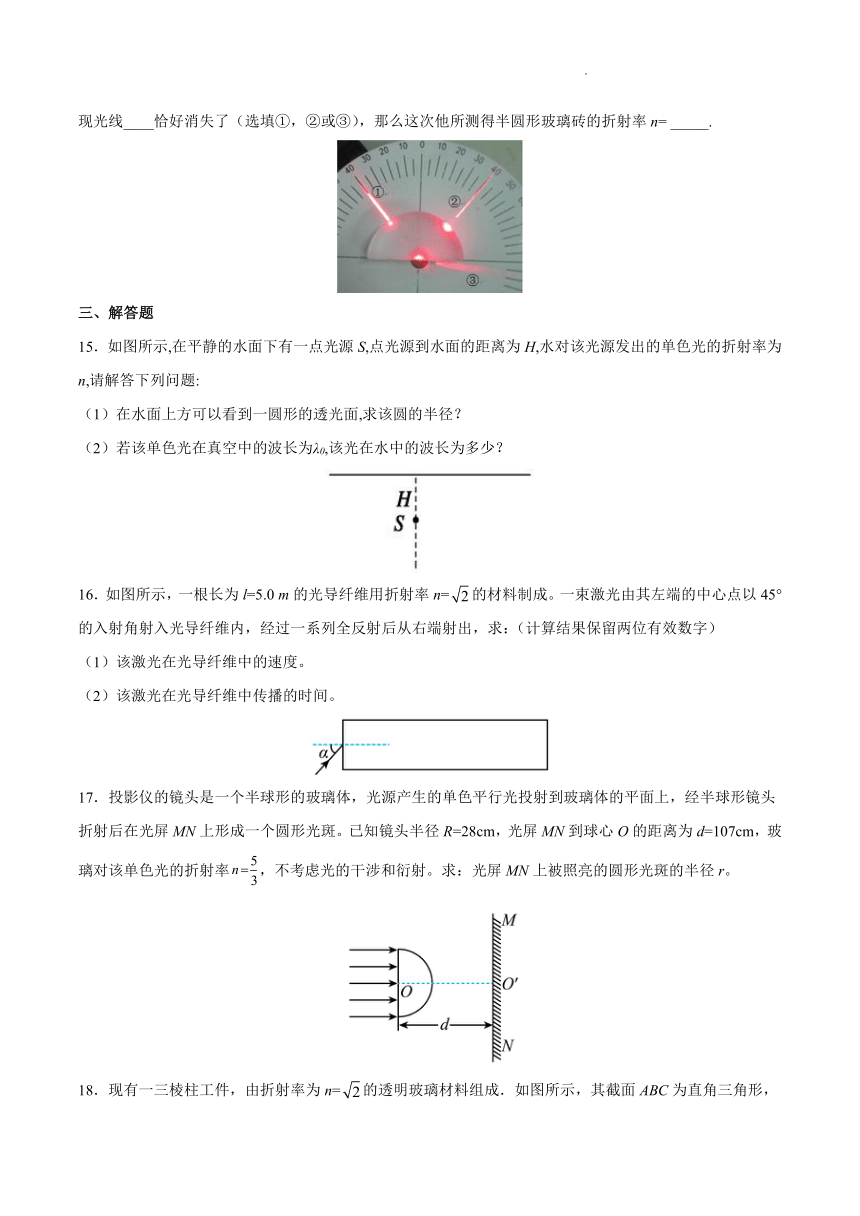
14.小李同学利用激光笔和角度圆盘测量半圆形玻璃砖的折射率,如图2所示是他采用手机拍摄的某次实验现象图,红色是三条光线,固定好激光笔,然后将圆盘和玻璃砖一起顺时针绕圆心缓慢转动了50角,发现光线____恰好消失了(选填①,②或③),那么这次他所测得半圆形玻璃砖的折射率n= _____.
三、解答题
15.如图所示,在平静的水面下有一点光源S,点光源到水面的距离为H,水对该光源发出的单色光的折射率为n,请解答下列问题:
(1)在水面上方可以看到一圆形的透光面,求该圆的半径?
(2)若该单色光在真空中的波长为λ0,该光在水中的波长为多少?
16.如图所示,一根长为l=5.0 m的光导纤维用折射率n=的材料制成。一束激光由其左端的中心点以45°的入射角射入光导纤维内,经过一系列全反射后从右端射出,求:(计算结果保留两位有效数字)
(1)该激光在光导纤维中的速度。
(2)该激光在光导纤维中传播的时间。
17.投影仪的镜头是一个半球形的玻璃体,光源产生的单色平行光投射到玻璃体的平面上,经半球形镜头折射后在光屏MN上形成一个圆形光斑。已知镜头半径R=28cm,光屏MN到球心O的距离为d=107cm,玻璃对该单色光的折射率,不考虑光的干涉和衍射。求:光屏MN上被照亮的圆形光斑的半径r。
18.现有一三棱柱工件,由折射率为n=的透明玻璃材料组成.如图所示,其截面ABC为直角三角形,∠ACB=30°.现有一条光线沿着截面从AC边上的O点以45°的入射角射入工件,折射后到达BC边.求:
(1)光线射入工件时的折射角;
(2)光线第一次射出工件时与界面的夹角
19.一公园的湖面上修建了一个伸向水面的观景平台,如图所示为其竖直截面图,水平湖底上的P点位于观景平台右侧边缘正下方,观景平台下表面距湖底的高度为H=8m,在距观景平台右侧边缘正前方d=8m处有垂直湖面足够大的宣传布幕在P点左侧l=6m处湖上的Q点安装有一单色光光源(可视为点光源)。已知水对该单色光的折射率,当水面与观景平台的下表面齐平时,只考虑在图中截面内传播的光,求:
(1)该光源发出的光照射到布幕上的最高点距水面的高度h;
(2)该光源发出的光能射出水面的最远位置距观景平台右侧的最远距离s(结果可用根号表示)。
参考答案
1.D 2.B 3.D 4.B 5.B 6.B 7.A 8.A
9.D 10.A 11.BD 12.BC 13.BD
14. ③
15.(1) (2)
【解析】
(1)设光在水面发生全反射的临界角为C,透光面的半径为r,则:,则,根据数学知识,得: ,解得:
(2)根据光传播过程中频率不变,由公式,折射率与速度关系: ,联立解得,光在水中的波长为
16.(1)2.1×108 m/s;(2)2.7×10-8 s。
【解析】
(1)由
可得v≈2.1×108 m/s
(2)激光在光导纤维中光路图如图所示,由
并结合几何知识得
大于临界角45°,因此发生全反射。同理光线每次在侧面都将发生全反射,直到光线到达右端面。
由于
得
故光线在光导纤维中传播的距离为s=l
因此该激光在光导纤维中传播所经历的时间
t=
t≈2.7×10-8 s
17.0.96m
【解析】
如图所示,设光线入射到D点时恰好发生全反射
由,在△ODF中
在△中
又
解得
18.(1);(2) 90°
【解析】
(1)由折射定律
代入得AC界面折射角
(2)根据平面几何关系,BC界面入射角为60°
光线在BC界面发生全反射,从AB界面垂直射出,故光线进入第一次射出界面与界面的夹角为90°
19.(1)h=6m;(2)
【解析】
(1)发生折射如图所示
在直角三角形OPQ中H=8m,1=6m,则OQ=10m,sinr=0.6
由,得sini=0.8
由d=8m得OA=10m,AB=6m
即h=6m
(2)光源在水面的光斑最远处为发生全反射的情况,如图所示
由,得sinC=
则,tanC=
得答案第1页,共2页
一、选择题
1.已知介质对某单色光的临界角为C,则不正确的是( )
A.该介质对单色光的折射率等于
B.此单色光在该介质中的传播速度等于csinC(c是光在真空中的传播速度)
C.此单色光在该介质中的传播波长是在真空中波长的sinC倍
D.此单色光在该介质中的频率是在真空中的倍
2.光线由某种媒质射向与空气的分界面,当入射角大于450时折射光线消失,由此可断定这种媒质的折射率是( )
A. B. C. D.n=2
3.公路交通标志牌是由基板和附着在基板上的反光膜组成,反光膜一般由镀在玻璃微珠上的铝层组成,夜间能将汽车射来的灯光反射回去,使司机看清交通标志.交通标志牌的结构示意图如图,这种交通标志牌的原理是( )
A.利用了光的反射
B.利用了光的折射
C.利用了光的色散
D.利用了光的全反射
4.一束光从某介质进入真空,方向如图所示,则下列判断中正确的是( )
A.该介质的折射率是
B.该介质的折射率是
C.该介质相对真空发生全反射的临界角是45°
D.光线从介质射入真空的过程中,无论怎样改变入射方向都不可能发生全反射现象
5.自行车上的红色尾灯不仅是装饰品,也是夜间骑车的安全指示灯,它能把来自后面的光照反射回去,某种自行车尾灯可简化为由许多整齐排列的等腰直角棱镜(折射率n>)组成,棱镜的横截面如图所示,一平行于横截面的光线从O点垂直AB边射入棱镜,先后经过AC和CB边反射后,从AB边的O′点射出,则出射光线是( )
A.平行于AC边的光线① B.平行于入射光线的光线②
C.平行于CB边的光线③ D.沿AB边的光线④
6.空气中两条光线a和b从方框左侧入射,分别从方框下方和上方射出,其框外光线如图所示。方框内有两个折射率n=1.5的玻璃全反射棱镜。下列选项中给出了两棱镜四种放置方式的示意图,其中能产生上述效果的是 ( )
A. B. C. D.
7.如图所示,一块上、下表面平行的玻璃砖的厚度为L,玻璃砖的折射率n=,若光从上表面AB射入的入射角i=60°,光在真空中的光速为c,则( )
A.折射角r=30°
B.光在玻璃中传播的时间为
C.光在玻璃中传播的时间为
D.改变入射角i,光在下表面CD可能发生全发射
8.“半潜艇”船体主要部分浸入水中,甲板始终浮出水面,潜艇内的乘客处在海平面以下,可以通过玻璃窗观察水中景物(如图1),原理图2,已知该处海水的折射率为,潜艇玻璃表面和水面垂直,且玻璃的厚度可以忽略,则以下说法中不正确的是( )
A.游客在潜艇内部看到正前方的鱼比实际位置要远一些
B.潜艇正前方的鱼看到潜艇中的人比实际位置要远一些
C.水面上方射入水中的光线不能照射到潜艇内部
D.潜艇内游客用手电筒朝水中照射时,水面上的人不可能看到手电筒发出的光
9.在完全透明的水下某深处,放一点光源,在水面上可见到一个圆形的透光圆面,若透光圆面的半径匀速增大,则光源正( )
A.加速上长 B.加速下降 C.匀速上升 D.匀速下降
10.2009年诺贝尔物理学奖授予英国华裔物理学家高锟,以表彰他在光纤通信研究中的突出贡献.光纤通信是利用了光的全反射的原理,光导纤维由内芯和外套两层组成.下列有关光导纤维的说法中正确的是( )
A.内芯的折射率比外套大,光传播时在内芯与外套的界面发生全反射
B.内芯的折射率比外套小,光传播时在内芯与外套的界面发生全反射
C.内芯的折射率比外套小,光传播时在内芯与外套的界面发生折射
D.内芯的折射率与外套相同,外套的材料有韧性,可以对内芯起保护作用
11.下列说法正确的是( )
A.因为水的密度大于酒精的密度,所以水是光密介质
B.因为水的折射率小于酒精的折射率,所以水对酒精来说是光疏介质
C.同一束光在光密介质中的传播速度较大
D.同一束光在光密介质中的传播速度较小
12.如图是在四川景区九寨沟拍摄的一张风景照片,湖水清澈见底,近处湖面水下的树枝和池底都看得很清楚,而远处则只看到对岸山峰和绿树的倒影,水面下的景物则根本看不到.下列说法中正确的是( )
A.远处山峰的倒影非常清晰,是因为来自山峰的光线在水面上发生了全反射
B.光从空气射入水中,光的波速变小,波长变小
C.远处水面下景物的光线到水面处,入射角较大,可能发生了全反射,所以看不见
D.来自近处水面下景物的光射到水面处,入射角较小,反射光强而折射光弱,因此有较多的能量射出水面而进入人的眼睛中
13.某大学研制出了正六棱柱“隐形衣”,有同学将正六棱柱放进装满水的透明鱼缸,向着棱的方向看,可以看到鱼缸另一侧大学的校徽;用一支铅笔穿过正六棱柱中心轴线的孔洞,再向棱方向观察,铅笔插进孔洞的那段消失不见了(如图甲所示,图乙为光路说明图),关于此实验说法正确的是( )
A.隐形的原理是光发生了全反射
B.光由水进入该介质,折射角大于入射角
C.隐形的原理是光被玻璃吸收了
D.光在该介质中的传播的速度大于在水中传播速度
二、填空题
14.小李同学利用激光笔和角度圆盘测量半圆形玻璃砖的折射率,如图2所示是他采用手机拍摄的某次实验现象图,红色是三条光线,固定好激光笔,然后将圆盘和玻璃砖一起顺时针绕圆心缓慢转动了50角,发现光线____恰好消失了(选填①,②或③),那么这次他所测得半圆形玻璃砖的折射率n= _____.
三、解答题
15.如图所示,在平静的水面下有一点光源S,点光源到水面的距离为H,水对该光源发出的单色光的折射率为n,请解答下列问题:
(1)在水面上方可以看到一圆形的透光面,求该圆的半径?
(2)若该单色光在真空中的波长为λ0,该光在水中的波长为多少?
16.如图所示,一根长为l=5.0 m的光导纤维用折射率n=的材料制成。一束激光由其左端的中心点以45°的入射角射入光导纤维内,经过一系列全反射后从右端射出,求:(计算结果保留两位有效数字)
(1)该激光在光导纤维中的速度。
(2)该激光在光导纤维中传播的时间。
17.投影仪的镜头是一个半球形的玻璃体,光源产生的单色平行光投射到玻璃体的平面上,经半球形镜头折射后在光屏MN上形成一个圆形光斑。已知镜头半径R=28cm,光屏MN到球心O的距离为d=107cm,玻璃对该单色光的折射率,不考虑光的干涉和衍射。求:光屏MN上被照亮的圆形光斑的半径r。
18.现有一三棱柱工件,由折射率为n=的透明玻璃材料组成.如图所示,其截面ABC为直角三角形,∠ACB=30°.现有一条光线沿着截面从AC边上的O点以45°的入射角射入工件,折射后到达BC边.求:
(1)光线射入工件时的折射角;
(2)光线第一次射出工件时与界面的夹角
19.一公园的湖面上修建了一个伸向水面的观景平台,如图所示为其竖直截面图,水平湖底上的P点位于观景平台右侧边缘正下方,观景平台下表面距湖底的高度为H=8m,在距观景平台右侧边缘正前方d=8m处有垂直湖面足够大的宣传布幕在P点左侧l=6m处湖上的Q点安装有一单色光光源(可视为点光源)。已知水对该单色光的折射率,当水面与观景平台的下表面齐平时,只考虑在图中截面内传播的光,求:
(1)该光源发出的光照射到布幕上的最高点距水面的高度h;
(2)该光源发出的光能射出水面的最远位置距观景平台右侧的最远距离s(结果可用根号表示)。
参考答案
1.D 2.B 3.D 4.B 5.B 6.B 7.A 8.A
9.D 10.A 11.BD 12.BC 13.BD
14. ③
15.(1) (2)
【解析】
(1)设光在水面发生全反射的临界角为C,透光面的半径为r,则:,则,根据数学知识,得: ,解得:
(2)根据光传播过程中频率不变,由公式,折射率与速度关系: ,联立解得,光在水中的波长为
16.(1)2.1×108 m/s;(2)2.7×10-8 s。
【解析】
(1)由
可得v≈2.1×108 m/s
(2)激光在光导纤维中光路图如图所示,由
并结合几何知识得
大于临界角45°,因此发生全反射。同理光线每次在侧面都将发生全反射,直到光线到达右端面。
由于
得
故光线在光导纤维中传播的距离为s=l
因此该激光在光导纤维中传播所经历的时间
t=
t≈2.7×10-8 s
17.0.96m
【解析】
如图所示,设光线入射到D点时恰好发生全反射
由,在△ODF中
在△中
又
解得
18.(1);(2) 90°
【解析】
(1)由折射定律
代入得AC界面折射角
(2)根据平面几何关系,BC界面入射角为60°
光线在BC界面发生全反射,从AB界面垂直射出,故光线进入第一次射出界面与界面的夹角为90°
19.(1)h=6m;(2)
【解析】
(1)发生折射如图所示
在直角三角形OPQ中H=8m,1=6m,则OQ=10m,sinr=0.6
由,得sini=0.8
由d=8m得OA=10m,AB=6m
即h=6m
(2)光源在水面的光斑最远处为发生全反射的情况,如图所示
由,得sinC=
则,tanC=
得答案第1页,共2页
