27.2.3相似三角形的周长与面积课件
文档属性
| 名称 | 27.2.3相似三角形的周长与面积课件 |
|
|
| 格式 | zip | ||
| 文件大小 | 703.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-12 18:46:00 | ||
图片预览






文档简介
课件20张PPT。回顾旧知相似三角形有哪些性质?27.2.3相似三角形的周长与面积〔教学目标〕
1. 经历探索相似三角形性质的过程,并在探究过程中发展学生积极的情感、态度、价值观,体验解决问题策略的多样性。
2.理解并掌握相似三角形周长的比等于相似比、面积比等于相似比的平方,并能用来解决简单的问题。
3.探索相似多边形周长的比等于相似比、面积比等于相似比的平方,体验化归思想。
〔教学重点与难点〕
重点:理解并掌握相似三角形周长的比等于相似比、面积比等于相似比的平方。
难点:探索相似多边形周长的比等于相似比、面积比等于相似比的平方。(1)相似三角形对应角相等。
(2)相似三角形对应边成比例。
(3)相似三角形对应高的比等于相似比。
(4)相似三角形对应中线的比等于相似比。
(5)相似三角形对应角平分线的比等于相似比。相似三角形的性质k相似三角形的周长有什么关系?相似三角形的面积有什么关系?教学目标 理解并掌握相似三角形周长的比等于相似比、面积比等于相似比的平方,并能用来解决简单的问题。 探索相似多边形周长的比等于相似比、面积比等于相似比的平方,体验化归思想。经历探索相似三角形性质的过程,并在探究过程中发展学生积极的情感、态度、价值观,体验解决问题策略的多样性。教学重难点 理解并掌握相似三角形周长的比等于相似比、面积比等于相似比的平方。
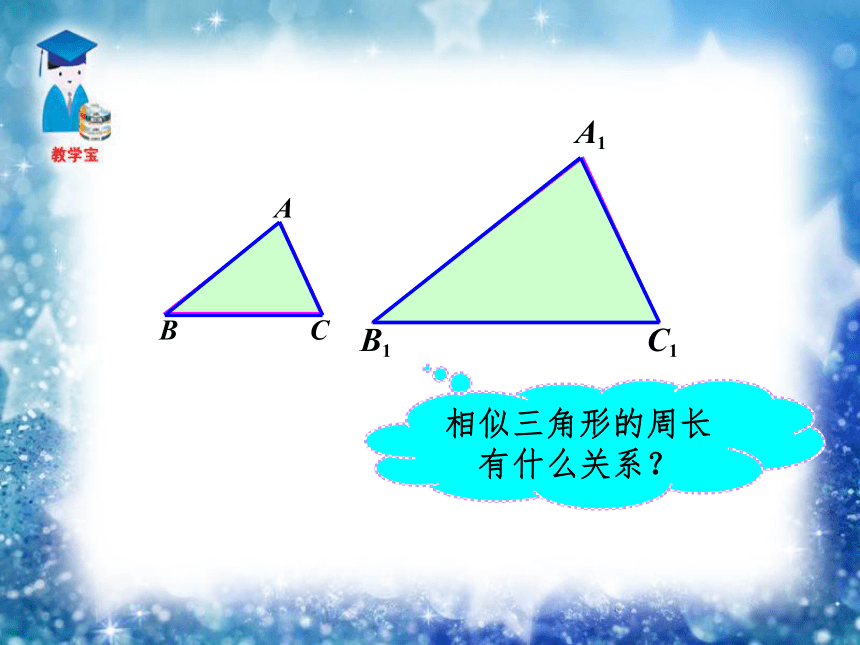
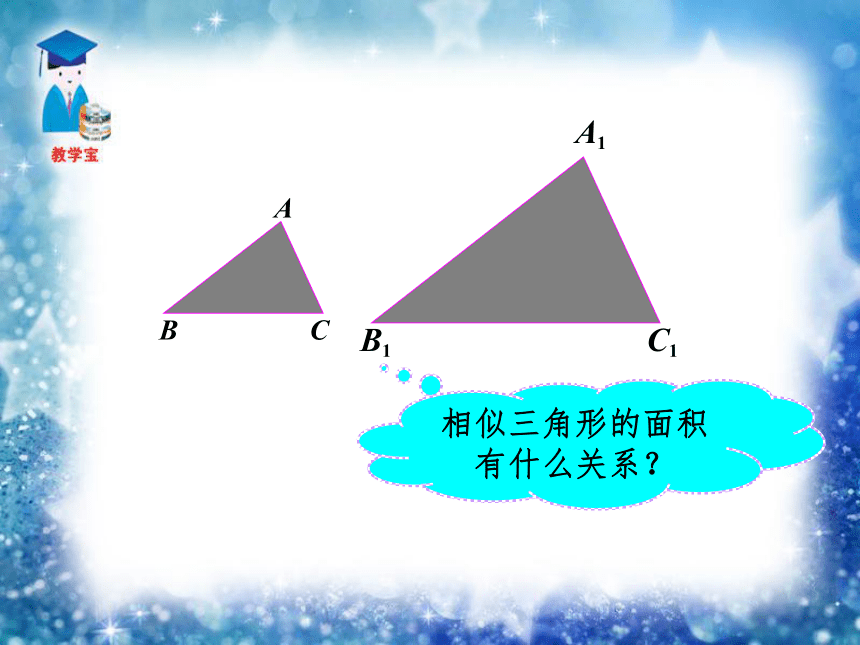
探索相似多边形周长的比等于相似比、面积比等于相似比的平方。(等比性质)C△ABC = AB+BC+CA周长:C△A1B1C1 = A1B1+B1C1+C1A1∵∴∴相似三角形周长的比等于相似比。六边形ABCDEF∽六边形A1B1C1D1E1F1,且相似比是k。相似多边形周长的比等于相似比。S△ABC =面积:S△A1B1C1 =∵∴∴相似三角形面积的比等于相似比的平方。DD127.2.1中,我们知道对应高之比等于相似比。=== k2相似三角形面积的比等于相似比的平方。同理:课堂小结 对应角相等。
对应边成比例。
对应高的比等于相似比。
对应中线的比等于相似比。
对应角平分线的比等于相似比。
周长比等于相似比。
面积比等于相似比的平方。相似三角形(多边形)的性质:1. 已知两个三角形相似,请完成下列表格。41610101004kkk2随堂练习 2. 如果两个相似三角形的面积之比为1:9,则它们对应边的比为______,对应高的比为______ ,周长的比为______ 。
3. 如果两个相似三角形的面积之比为2:7,较大三角形一边上的高为7,则较小三角形对应边上的高为______ 。1:31:31:3 4. 这是圆桌正上方的灯泡(当成一个点)发出的光线照射桌面形成阴影的示意图,已知桌面的直径为1.2米,桌面距离地面为1米,若灯泡距离地面3米,则地面上阴影部分的面积为多少? 5. △ABC中,DE∥BC,EF∥AB,已知△ADE和△EFC的面积分别为4和9,求△ABC的面积。习题答案1. 其他两边的实际长度都是20m.
2. (1)相似,因为对应边的比相等;
(2)不一定相似,因为相等的角的夹边的比不相等;
(3)相似,因为有两组对应角相等.
3. (1)相似;(2)相似,x=40.5,y=98.
1. 经历探索相似三角形性质的过程,并在探究过程中发展学生积极的情感、态度、价值观,体验解决问题策略的多样性。
2.理解并掌握相似三角形周长的比等于相似比、面积比等于相似比的平方,并能用来解决简单的问题。
3.探索相似多边形周长的比等于相似比、面积比等于相似比的平方,体验化归思想。
〔教学重点与难点〕
重点:理解并掌握相似三角形周长的比等于相似比、面积比等于相似比的平方。
难点:探索相似多边形周长的比等于相似比、面积比等于相似比的平方。(1)相似三角形对应角相等。
(2)相似三角形对应边成比例。
(3)相似三角形对应高的比等于相似比。
(4)相似三角形对应中线的比等于相似比。
(5)相似三角形对应角平分线的比等于相似比。相似三角形的性质k相似三角形的周长有什么关系?相似三角形的面积有什么关系?教学目标 理解并掌握相似三角形周长的比等于相似比、面积比等于相似比的平方,并能用来解决简单的问题。 探索相似多边形周长的比等于相似比、面积比等于相似比的平方,体验化归思想。经历探索相似三角形性质的过程,并在探究过程中发展学生积极的情感、态度、价值观,体验解决问题策略的多样性。教学重难点 理解并掌握相似三角形周长的比等于相似比、面积比等于相似比的平方。
探索相似多边形周长的比等于相似比、面积比等于相似比的平方。(等比性质)C△ABC = AB+BC+CA周长:C△A1B1C1 = A1B1+B1C1+C1A1∵∴∴相似三角形周长的比等于相似比。六边形ABCDEF∽六边形A1B1C1D1E1F1,且相似比是k。相似多边形周长的比等于相似比。S△ABC =面积:S△A1B1C1 =∵∴∴相似三角形面积的比等于相似比的平方。DD127.2.1中,我们知道对应高之比等于相似比。=== k2相似三角形面积的比等于相似比的平方。同理:课堂小结 对应角相等。
对应边成比例。
对应高的比等于相似比。
对应中线的比等于相似比。
对应角平分线的比等于相似比。
周长比等于相似比。
面积比等于相似比的平方。相似三角形(多边形)的性质:1. 已知两个三角形相似,请完成下列表格。41610101004kkk2随堂练习 2. 如果两个相似三角形的面积之比为1:9,则它们对应边的比为______,对应高的比为______ ,周长的比为______ 。
3. 如果两个相似三角形的面积之比为2:7,较大三角形一边上的高为7,则较小三角形对应边上的高为______ 。1:31:31:3 4. 这是圆桌正上方的灯泡(当成一个点)发出的光线照射桌面形成阴影的示意图,已知桌面的直径为1.2米,桌面距离地面为1米,若灯泡距离地面3米,则地面上阴影部分的面积为多少? 5. △ABC中,DE∥BC,EF∥AB,已知△ADE和△EFC的面积分别为4和9,求△ABC的面积。习题答案1. 其他两边的实际长度都是20m.
2. (1)相似,因为对应边的比相等;
(2)不一定相似,因为相等的角的夹边的比不相等;
(3)相似,因为有两组对应角相等.
3. (1)相似;(2)相似,x=40.5,y=98.
