15.5.1提公因式法
图片预览








文档简介
课件22张PPT。提公因式法义务教育课程标准实验教科书八年级上册 一、教材分析
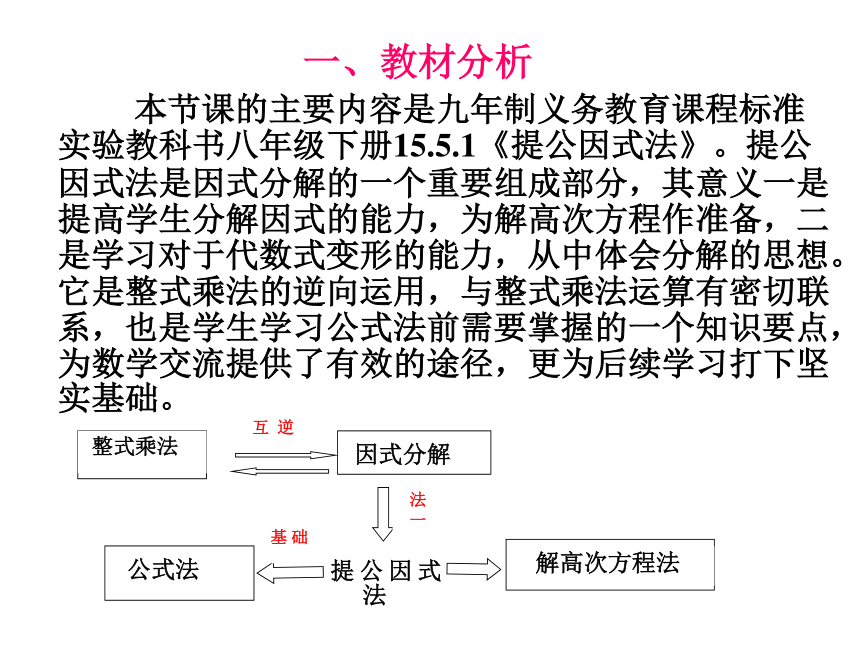
本节课的主要内容是九年制义务教育课程标准实验教科书八年级下册15.5.1《提公因式法》。提公因式法是因式分解的一个重要组成部分,其意义一是提高学生分解因式的能力,为解高次方程作准备,二是学习对于代数式变形的能力,从中体会分解的思想。它是整式乘法的逆向运用,与整式乘法运算有密切联系,也是学生学习公式法前需要掌握的一个知识要点,为数学交流提供了有效的途径,更为后续学习打下坚实基础。互 逆提公因式法法 一基 础 整式乘法因式分解公式法 解高次方程法 二说教学目标
1.知识与技能
1)了解因式分解(分解因式)、公因式和提公因式法的概念;
2)能确定多项式各项的公因式;
3)会用提公因式法把多项式分解因式。
2.过程与方法
1)经历对实际问题的解决,了解分解因式的意义,提高自身的直觉思维的思想方法;
2)寻找确定公因式的三步曲,经历解决问题“逐个击破”的思维过程。
3.情感态度与价值观
1)感受分解因式的简便快速,形成生活中解决问题寻找最佳方法的意识;
2)通过教师的启发,培养独立思考的习惯,提高合作交流意识,增加学好数学的信心。 三学情分析
1.学生已经学习过数的分解,我们借助数的分解引出因式分解,有助于学生的理解;
2.学生已经在第一章学习过整式乘法,而因式分解是整式乘法的逆运算,只要教师注意引导和强调,学生理解这个概念不难;
3.在提公因式法中提取字母中的“字母”可以是单项式、也可以是多项式,这一知识点学生较难理解,教师应注意引导;
4.在类似于例3这种题目中,学生第一感觉就会是先把式子全部展开,在这里教师应该要注意向学生渗透整体思想,让学生学会添括号,改变学生的惯性思维。四重点难点
重点:找公因式,会用提取公因式法进行因式分解。
难点:用提取公因式法进行因式分解。
关键点:找出多项式各项公因式。
五说教法学法
教法分析:启发式探究法
学法分析:采用自主探索、合作交流的研讨式学习方式。630能被哪些数整除?说说你是怎样想的。分析:可以把630分解成质数的乘积
的形式,即630=2×32×5×7运用已学过的知识填空:
⑴ x(x+1)= ;
⑵ (x+1)(x-1)= ;
⑶ (a+b)2= .回忆x2+xx2-1a2+2ab+b2
⑴ x2+x= ;
⑵ x2-1= ;
⑶ a2+2ab+b2= .
x(x+1)(x+1)(x-1)(a+b)2右边的空你会填吗探究思考观察“回忆”与“探究”,你能发现它们之间
的联系与区别吗?回忆
⑴ x(x+1)= x2+x ;
⑵ (x+1)(x-1)= x2-1 ;
⑶ (a+b)2= a2+2ab+b2 .探究
⑴ x2+x= x(x+1) ;
⑵ x2-1= (x+1)(x-1) ;
⑶ a2+2ab+b2= (a+b)2 . 把一个多项式化为几个整式的
乘积形式,像这样的式子的变形叫做把这个多项式因式分解,也叫做把这个多项式分解因式。乘积x2-1 (x+1)(x-1)因式分解整式乘法下列各式从左到右哪些是因式分解?
① m2-m=m(m-1) ( )?
② x(x-y)=x2-xy? ( ) ?
③ (a+3)(a-3)=a2-9 ( )
④ a2-2a+1=a(a-2)+1 ( )
⑤ x2-4x+4=(x-2)2 ( )是不是不是不是是15.5.1 提公因式法 问题:ma+mb+mc 这个多项 式有什么特征? m是这个多项式各项都含有的因式。注意:
公因式是多项式中各项都含有的公共的因式 。m(a+b+c)=ma+mb+mc ( )
ma+mb+mc=m(a+b+c) ( ) 像这样,将多项式 ma+mb+mc写成 m(a+b+c)的
形式,这种分解因式的方法叫做提公因式法。 乘法的分配律因式分解例1: 找出3 x 2 – 6 x 的公因式。系数:各项系数的最大公约数。3字母:各项的相同字母
x 所以,公因式是3x 。指数:相同字母 的最低次幂1
①ax+ay+a?????
②3mx-6nx2?????????
③4a2b+10ab2????????????
④x4y3+x3y3? ??
⑤12x2yz-9x3y2? 找公因式的方法:
①系数取各系数
的最大公约数;
②字母取各项的
相同字母,而且
各字母的指数取
次数最低的。 指出下列各多项式中各项的公因式:a公因式3x2abx3y33x2y课堂练习一例2:把8a3b2+12ab3c分解因式 .注意:提公因式后,另一个因式:
①项数应与原多项式的项数一样;
②不再含有公因式。 分析:先找出各项的公因式,然后再分解.解: 8a3b2+12ab3c
=4ab2.2a2+ 4ab2 .3bc
= 4ab 2 (2a2 + 3bc)公因式: 4ab2把下列各式分解因式:
⑴ x2+x6 ; ⑵ 8m2n+2mn;
⑶ 12xyz-9x2y2. 课堂练习二解: ⑴ x2+x6
=x2(1+x4)⑵ 8m2n+2mn
=2mn(4m+1)⑶ 12xyz-9x2y2
=3xy(4z-3xy)例3:把2a(b+c)-3(b+c)分解因式 (b+c)(b+c)解: 2a(b+c)-3(b+c)
= (b+c)(2a-3) 注意:公因式可以是数字,字母,也 可以是单项式,还可以是多项式。4a2(x+7)-3(X+7),其中a=-5,x=3课堂练习三先分解因式,再求值。解: 4a2(x+7)-3(x+7)
= (x+7)( 4a2 -3)当a=-5,x=3时,
原式=(3+7)〔4×(-5)2-3〕
=10×(100 -3)
=970课堂小结本节课你学到了些什么?
有哪些收获?作业:
亲爱的同学们,再见!
本节课的主要内容是九年制义务教育课程标准实验教科书八年级下册15.5.1《提公因式法》。提公因式法是因式分解的一个重要组成部分,其意义一是提高学生分解因式的能力,为解高次方程作准备,二是学习对于代数式变形的能力,从中体会分解的思想。它是整式乘法的逆向运用,与整式乘法运算有密切联系,也是学生学习公式法前需要掌握的一个知识要点,为数学交流提供了有效的途径,更为后续学习打下坚实基础。互 逆提公因式法法 一基 础 整式乘法因式分解公式法 解高次方程法 二说教学目标
1.知识与技能
1)了解因式分解(分解因式)、公因式和提公因式法的概念;
2)能确定多项式各项的公因式;
3)会用提公因式法把多项式分解因式。
2.过程与方法
1)经历对实际问题的解决,了解分解因式的意义,提高自身的直觉思维的思想方法;
2)寻找确定公因式的三步曲,经历解决问题“逐个击破”的思维过程。
3.情感态度与价值观
1)感受分解因式的简便快速,形成生活中解决问题寻找最佳方法的意识;
2)通过教师的启发,培养独立思考的习惯,提高合作交流意识,增加学好数学的信心。 三学情分析
1.学生已经学习过数的分解,我们借助数的分解引出因式分解,有助于学生的理解;
2.学生已经在第一章学习过整式乘法,而因式分解是整式乘法的逆运算,只要教师注意引导和强调,学生理解这个概念不难;
3.在提公因式法中提取字母中的“字母”可以是单项式、也可以是多项式,这一知识点学生较难理解,教师应注意引导;
4.在类似于例3这种题目中,学生第一感觉就会是先把式子全部展开,在这里教师应该要注意向学生渗透整体思想,让学生学会添括号,改变学生的惯性思维。四重点难点
重点:找公因式,会用提取公因式法进行因式分解。
难点:用提取公因式法进行因式分解。
关键点:找出多项式各项公因式。
五说教法学法
教法分析:启发式探究法
学法分析:采用自主探索、合作交流的研讨式学习方式。630能被哪些数整除?说说你是怎样想的。分析:可以把630分解成质数的乘积
的形式,即630=2×32×5×7运用已学过的知识填空:
⑴ x(x+1)= ;
⑵ (x+1)(x-1)= ;
⑶ (a+b)2= .回忆x2+xx2-1a2+2ab+b2
⑴ x2+x= ;
⑵ x2-1= ;
⑶ a2+2ab+b2= .
x(x+1)(x+1)(x-1)(a+b)2右边的空你会填吗探究思考观察“回忆”与“探究”,你能发现它们之间
的联系与区别吗?回忆
⑴ x(x+1)= x2+x ;
⑵ (x+1)(x-1)= x2-1 ;
⑶ (a+b)2= a2+2ab+b2 .探究
⑴ x2+x= x(x+1) ;
⑵ x2-1= (x+1)(x-1) ;
⑶ a2+2ab+b2= (a+b)2 . 把一个多项式化为几个整式的
乘积形式,像这样的式子的变形叫做把这个多项式因式分解,也叫做把这个多项式分解因式。乘积x2-1 (x+1)(x-1)因式分解整式乘法下列各式从左到右哪些是因式分解?
① m2-m=m(m-1) ( )?
② x(x-y)=x2-xy? ( ) ?
③ (a+3)(a-3)=a2-9 ( )
④ a2-2a+1=a(a-2)+1 ( )
⑤ x2-4x+4=(x-2)2 ( )是不是不是不是是15.5.1 提公因式法 问题:ma+mb+mc 这个多项 式有什么特征? m是这个多项式各项都含有的因式。注意:
公因式是多项式中各项都含有的公共的因式 。m(a+b+c)=ma+mb+mc ( )
ma+mb+mc=m(a+b+c) ( ) 像这样,将多项式 ma+mb+mc写成 m(a+b+c)的
形式,这种分解因式的方法叫做提公因式法。 乘法的分配律因式分解例1: 找出3 x 2 – 6 x 的公因式。系数:各项系数的最大公约数。3字母:各项的相同字母
x 所以,公因式是3x 。指数:相同字母 的最低次幂1
①ax+ay+a?????
②3mx-6nx2?????????
③4a2b+10ab2????????????
④x4y3+x3y3? ??
⑤12x2yz-9x3y2? 找公因式的方法:
①系数取各系数
的最大公约数;
②字母取各项的
相同字母,而且
各字母的指数取
次数最低的。 指出下列各多项式中各项的公因式:a公因式3x2abx3y33x2y课堂练习一例2:把8a3b2+12ab3c分解因式 .注意:提公因式后,另一个因式:
①项数应与原多项式的项数一样;
②不再含有公因式。 分析:先找出各项的公因式,然后再分解.解: 8a3b2+12ab3c
=4ab2.2a2+ 4ab2 .3bc
= 4ab 2 (2a2 + 3bc)公因式: 4ab2把下列各式分解因式:
⑴ x2+x6 ; ⑵ 8m2n+2mn;
⑶ 12xyz-9x2y2. 课堂练习二解: ⑴ x2+x6
=x2(1+x4)⑵ 8m2n+2mn
=2mn(4m+1)⑶ 12xyz-9x2y2
=3xy(4z-3xy)例3:把2a(b+c)-3(b+c)分解因式 (b+c)(b+c)解: 2a(b+c)-3(b+c)
= (b+c)(2a-3) 注意:公因式可以是数字,字母,也 可以是单项式,还可以是多项式。4a2(x+7)-3(X+7),其中a=-5,x=3课堂练习三先分解因式,再求值。解: 4a2(x+7)-3(x+7)
= (x+7)( 4a2 -3)当a=-5,x=3时,
原式=(3+7)〔4×(-5)2-3〕
=10×(100 -3)
=970课堂小结本节课你学到了些什么?
有哪些收获?作业:
亲爱的同学们,再见!
