2021-2022学年北师大版八年级数学下册 1.1.3等腰三角形课件 (共22张PPT)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学下册 1.1.3等腰三角形课件 (共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-27 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
北师大版数学八年级(下)
课题:等腰三角形(3)
学习目标
1.掌握利用等腰三角形的性质对三角形进行判定的方法。
2.理解反证法的意义,掌握反证法的书写步骤,运用反证法进行证明。
复习引入
问题1:等腰三角形有怎样的性质?
角:等腰三角形的两底角相等.(定理)
(简写成 ‘‘等边对等角”)
三线: 等腰三角形的顶角的平分线、底边上的中线、 底边上的高互相重合(简写成 ‘‘三线合一”)(推论)
问题2:如何判定一个三角形是等腰三角形?
边:等腰三角形的两腰相等.(定义)
对称性:等腰三角形是轴对称图形
释疑解惑
问题2:如何判定一个三角形是等腰三角形?
边:
等腰三角形 两腰相等
性质
两边相等 等腰三角形
?
定义:有两条边相等的三角形是等腰三角形
判定
(定义判定法)
角:
等腰三角形 两底角相等
性质
两角相等 等腰三角形
?
等边对等角
释疑解惑
问题2:如何判定一个三角形是等腰三角形?
已知:△ABC中,∠B=∠C,
求证:AB=AC
证明一:作∠BAC的平分线AD,
∴ ∠1=∠2
在△BAD和△CAD中,
∠1=∠2,
∠B=∠C,
AD=AD
∴ △BAD≌ △CAD(AAS)
∴AB=AC(全等三角形的对应边相等)
证明:有两个角相等的三角形是等腰三角形。
A
B
C
D
1
2
释疑解惑
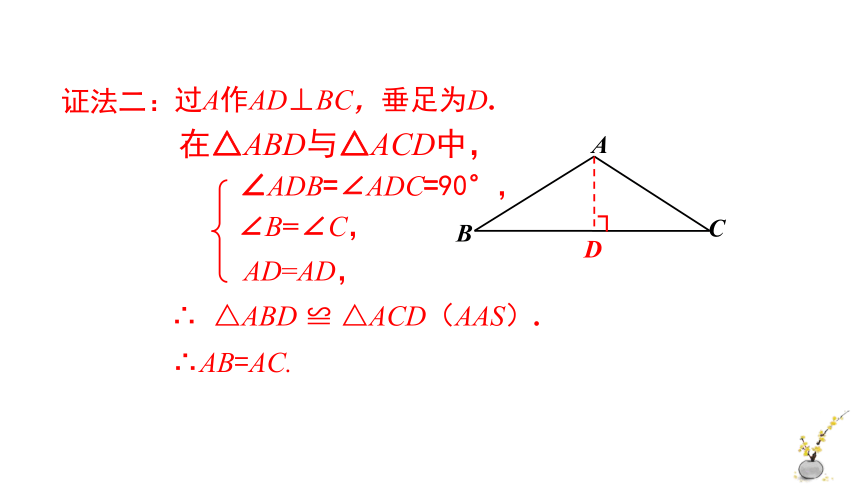
过A作AD⊥BC,垂足为D.
在△ABD与△ACD中,
∠ADB=∠ADC=90°,
∠B=∠C,
AD=AD,
∴ △ABD ≌ △ACD(AAS).
∴AB=AC.
C
A
B
D
┐
证法二:
证法三:
取BC中点,连接AD,过D点作DE⊥AB,DF⊥AC,垂足分别为E、F.
在△BDE与△CDF中,
∠BED=∠CFD=90°,
∠B=∠C,
BD=CD,
∴ △BDE ≌ △CDF(AAS).
∴BE=CF,DE=DF
∴AE=AF.
∴AE+BE=AF+CF.
∴AB=AC.
∵∠AED=∠AFD=90°,AD=AD
E
F
┐
C
A
B
D
┐
有两个角相等的三角形是等腰三角形.(等角对等边)
等腰三角形的判定定理:
符号语言:在△ABC中,∵∠B=∠C, ∴AB=AC.
等腰三角形的判定与性质的异同
相同点:都是在一个三角形中;
区别:判定是由角到边,性质是由边到角.
即:
典例赏析
例1:已知:如图,AB=DC,BD=CA,
求证:△AED是等腰三角形。
A
B
C
D
E
证明:∵AB=DC,BD=CA,AD=DA,
∴△ABD≌△DCA(SSS)
∴∠ADB=∠DAC(全等三角形的对应角相等)
∴AE=DE(等角对等边)
∴ △AED是等腰三角形。
例2:如图,在△ABC中,∠ACB=90°,CD是AB边上的高,AE是∠BAC的角平分线,AE与CD交于点F,求证:△CEF是等腰三角形.
解:∵在△ABC中,∠ACB=90°,
∴∠B+∠BAC=90°.
∵CD是AB边上的高,
∴∠ACD+∠BAC=90°,
∴∠B=∠ACD.
∵AE是∠BAC的角平分线,
∴∠BAE=∠EAC,
∵∠B+∠BAE=∠AEC,∠ACD+∠EAC=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
∴△CEF是等腰三角形.
探究二
已知:如图,在△ABC中,∠B≠∠C,
求证:AB≠AC.
证明:假设AB=AC,
根据“等边对等角”定理,
∴ ∠C=∠B,
而已知条件∠B≠∠C.
∴“∠C=∠B”与已知条件“∠B≠∠C”相矛盾,
因此AB≠AC.
总结归纳
在证明时,先假设命题的结论不成立,然后由此推导出了与已知或公理或已证明过的定理相矛盾,从而证明命题的结论一定成立.这种证明方法称为反证法.
用反证法证题的一般步骤
1.假设: 先假设命题的结论不成立;
2.归谬: 从这个假设出发,应用正确的推论方法,得出与
定义,公理、已证定理或已知条件相矛盾的结果;
3.结论: 由矛盾的结果判定假设不正确,从而肯定命题
的结论正确.
例3 用反证法证明:三角形中必有一个内角大于等于60度.
证明:假设∠A,∠B,∠C没有一个内角大于等于60°, 即每个内角都小于60°,则
∠A+∠B+∠C<60°+60°+60°<180°
这与“三角形内角和定理” 矛盾
∴假设 不成立.
∴一个三角形中必有一个内角大于等于60度
典例赏析
例4. 如图,在△ABC中,∠ABC=∠ACB,BO平分∠ABC,CO平分∠ACB。
(1)图中的△ABC和△BOC是等腰三角形吗?说一说你的理由。
是等腰三角形,理由:有两个角相等的三角形是等腰三角形。
∵BO、CO平分∠ABC、∠ACB,
∠ABC=∠ACB
∴∠ABO=∠OBC=∠ACO=∠OCB
能力拓展
例4. 如图,在△ABC中,∠ABC=∠ACB,BO平分∠ABC,CO平分∠ACB。
(2)过O点作平行于BC的直线,分别与AB、AC交于E、F两点,图中有____个等腰三角形,线段EF与线段BE、FC之间的数量关系为_________.
5
EF=BE+CF
∵BO、CO平分∠ABC、∠ACB,
∠ABC=∠ACB
∴∠EBO=∠OBC=∠FCO=∠OCB
∵EF∥BC
∴∠EOB=∠OBC,∠FOC=∠OCB
∴∠EBO=∠EOB,∠FOC=∠FCO
∴BE=EO,FO=FC
∴EF=EO+FO=BE+CF
△ABC、△AEF、△BEO、△CFO、△BOC.
例4. 如图,在△ABC中,∠ABC=∠ACB,BO平分∠ABC,CO平分∠ACB。
(3)若∠ABC与∠ACB不相等,其余条件不变,第(2)问的结论还成立吗?为什么。
证明:EF=BE+CF成立.理由如下:
∵BO、CO平分∠ABC、∠ACB,
∴∠EBO=∠OBC,∠FCO=∠OCB
∵EF∥BC
∴∠EOB=∠OBC,∠FOC=∠OCB
∴∠EBO=∠EOB,∠FOC=∠FCO
∴BE=EO,FO=FC(等角对等边)
∴EF=EO+FO=BE+CF
1 如图,∠B=∠C=36°,∠ADE=∠AED=72°,则图中的等腰三角形有( )
A.3个
B.4个
C.5个
D.6个
随堂检测
2、如图,在等边△ABC中,点D,E分别在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数.
(2)求证:DC=CF.
3.如图,在△ABC中,AB=AC,D为BC边的中点,F为CA的延长线上一点,连接AD,过点F作FG⊥BC于点G,并交AB于点E,
求证:(1)AD∥FG; (2)△AEF是等腰三角形.
证明:(1)∵AB=AC,D为BC边的中点,
∴AD⊥BC(三线合一)
∵FG⊥BC
∴AD∥FG(垂直于同一直线的两条直线平行)
(2)由(1)可知∠CAD=∠BAD
∵AD∥FG
∴∠CAD=∠F ∠BAD=∠FEA
∴∠F=∠FEA
∴AE=AF(等角对等边)
∴△AEF是等腰三角形。
1 等腰三角形的判定:
(1)有两边相等的三角形是等腰三角形;
(2)有两个角相等的三角形是等腰三角形.
2 利用反证法解题的一般步骤:
(1) 假设;
(2) 归谬:从假设出发,经过推理论证得出与已知、定理、公理等相矛盾的结果;
(3) 结论:肯定命题结论正确.
课堂小结
感谢聆听!
北师大版数学八年级(下)
课题:等腰三角形(3)
学习目标
1.掌握利用等腰三角形的性质对三角形进行判定的方法。
2.理解反证法的意义,掌握反证法的书写步骤,运用反证法进行证明。
复习引入
问题1:等腰三角形有怎样的性质?
角:等腰三角形的两底角相等.(定理)
(简写成 ‘‘等边对等角”)
三线: 等腰三角形的顶角的平分线、底边上的中线、 底边上的高互相重合(简写成 ‘‘三线合一”)(推论)
问题2:如何判定一个三角形是等腰三角形?
边:等腰三角形的两腰相等.(定义)
对称性:等腰三角形是轴对称图形
释疑解惑
问题2:如何判定一个三角形是等腰三角形?
边:
等腰三角形 两腰相等
性质
两边相等 等腰三角形
?
定义:有两条边相等的三角形是等腰三角形
判定
(定义判定法)
角:
等腰三角形 两底角相等
性质
两角相等 等腰三角形
?
等边对等角
释疑解惑
问题2:如何判定一个三角形是等腰三角形?
已知:△ABC中,∠B=∠C,
求证:AB=AC
证明一:作∠BAC的平分线AD,
∴ ∠1=∠2
在△BAD和△CAD中,
∠1=∠2,
∠B=∠C,
AD=AD
∴ △BAD≌ △CAD(AAS)
∴AB=AC(全等三角形的对应边相等)
证明:有两个角相等的三角形是等腰三角形。
A
B
C
D
1
2
释疑解惑
过A作AD⊥BC,垂足为D.
在△ABD与△ACD中,
∠ADB=∠ADC=90°,
∠B=∠C,
AD=AD,
∴ △ABD ≌ △ACD(AAS).
∴AB=AC.
C
A
B
D
┐
证法二:
证法三:
取BC中点,连接AD,过D点作DE⊥AB,DF⊥AC,垂足分别为E、F.
在△BDE与△CDF中,
∠BED=∠CFD=90°,
∠B=∠C,
BD=CD,
∴ △BDE ≌ △CDF(AAS).
∴BE=CF,DE=DF
∴AE=AF.
∴AE+BE=AF+CF.
∴AB=AC.
∵∠AED=∠AFD=90°,AD=AD
E
F
┐
C
A
B
D
┐
有两个角相等的三角形是等腰三角形.(等角对等边)
等腰三角形的判定定理:
符号语言:在△ABC中,∵∠B=∠C, ∴AB=AC.
等腰三角形的判定与性质的异同
相同点:都是在一个三角形中;
区别:判定是由角到边,性质是由边到角.
即:
典例赏析
例1:已知:如图,AB=DC,BD=CA,
求证:△AED是等腰三角形。
A
B
C
D
E
证明:∵AB=DC,BD=CA,AD=DA,
∴△ABD≌△DCA(SSS)
∴∠ADB=∠DAC(全等三角形的对应角相等)
∴AE=DE(等角对等边)
∴ △AED是等腰三角形。
例2:如图,在△ABC中,∠ACB=90°,CD是AB边上的高,AE是∠BAC的角平分线,AE与CD交于点F,求证:△CEF是等腰三角形.
解:∵在△ABC中,∠ACB=90°,
∴∠B+∠BAC=90°.
∵CD是AB边上的高,
∴∠ACD+∠BAC=90°,
∴∠B=∠ACD.
∵AE是∠BAC的角平分线,
∴∠BAE=∠EAC,
∵∠B+∠BAE=∠AEC,∠ACD+∠EAC=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
∴△CEF是等腰三角形.
探究二
已知:如图,在△ABC中,∠B≠∠C,
求证:AB≠AC.
证明:假设AB=AC,
根据“等边对等角”定理,
∴ ∠C=∠B,
而已知条件∠B≠∠C.
∴“∠C=∠B”与已知条件“∠B≠∠C”相矛盾,
因此AB≠AC.
总结归纳
在证明时,先假设命题的结论不成立,然后由此推导出了与已知或公理或已证明过的定理相矛盾,从而证明命题的结论一定成立.这种证明方法称为反证法.
用反证法证题的一般步骤
1.假设: 先假设命题的结论不成立;
2.归谬: 从这个假设出发,应用正确的推论方法,得出与
定义,公理、已证定理或已知条件相矛盾的结果;
3.结论: 由矛盾的结果判定假设不正确,从而肯定命题
的结论正确.
例3 用反证法证明:三角形中必有一个内角大于等于60度.
证明:假设∠A,∠B,∠C没有一个内角大于等于60°, 即每个内角都小于60°,则
∠A+∠B+∠C<60°+60°+60°<180°
这与“三角形内角和定理” 矛盾
∴假设 不成立.
∴一个三角形中必有一个内角大于等于60度
典例赏析
例4. 如图,在△ABC中,∠ABC=∠ACB,BO平分∠ABC,CO平分∠ACB。
(1)图中的△ABC和△BOC是等腰三角形吗?说一说你的理由。
是等腰三角形,理由:有两个角相等的三角形是等腰三角形。
∵BO、CO平分∠ABC、∠ACB,
∠ABC=∠ACB
∴∠ABO=∠OBC=∠ACO=∠OCB
能力拓展
例4. 如图,在△ABC中,∠ABC=∠ACB,BO平分∠ABC,CO平分∠ACB。
(2)过O点作平行于BC的直线,分别与AB、AC交于E、F两点,图中有____个等腰三角形,线段EF与线段BE、FC之间的数量关系为_________.
5
EF=BE+CF
∵BO、CO平分∠ABC、∠ACB,
∠ABC=∠ACB
∴∠EBO=∠OBC=∠FCO=∠OCB
∵EF∥BC
∴∠EOB=∠OBC,∠FOC=∠OCB
∴∠EBO=∠EOB,∠FOC=∠FCO
∴BE=EO,FO=FC
∴EF=EO+FO=BE+CF
△ABC、△AEF、△BEO、△CFO、△BOC.
例4. 如图,在△ABC中,∠ABC=∠ACB,BO平分∠ABC,CO平分∠ACB。
(3)若∠ABC与∠ACB不相等,其余条件不变,第(2)问的结论还成立吗?为什么。
证明:EF=BE+CF成立.理由如下:
∵BO、CO平分∠ABC、∠ACB,
∴∠EBO=∠OBC,∠FCO=∠OCB
∵EF∥BC
∴∠EOB=∠OBC,∠FOC=∠OCB
∴∠EBO=∠EOB,∠FOC=∠FCO
∴BE=EO,FO=FC(等角对等边)
∴EF=EO+FO=BE+CF
1 如图,∠B=∠C=36°,∠ADE=∠AED=72°,则图中的等腰三角形有( )
A.3个
B.4个
C.5个
D.6个
随堂检测
2、如图,在等边△ABC中,点D,E分别在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数.
(2)求证:DC=CF.
3.如图,在△ABC中,AB=AC,D为BC边的中点,F为CA的延长线上一点,连接AD,过点F作FG⊥BC于点G,并交AB于点E,
求证:(1)AD∥FG; (2)△AEF是等腰三角形.
证明:(1)∵AB=AC,D为BC边的中点,
∴AD⊥BC(三线合一)
∵FG⊥BC
∴AD∥FG(垂直于同一直线的两条直线平行)
(2)由(1)可知∠CAD=∠BAD
∵AD∥FG
∴∠CAD=∠F ∠BAD=∠FEA
∴∠F=∠FEA
∴AE=AF(等角对等边)
∴△AEF是等腰三角形。
1 等腰三角形的判定:
(1)有两边相等的三角形是等腰三角形;
(2)有两个角相等的三角形是等腰三角形.
2 利用反证法解题的一般步骤:
(1) 假设;
(2) 归谬:从假设出发,经过推理论证得出与已知、定理、公理等相矛盾的结果;
(3) 结论:肯定命题结论正确.
课堂小结
感谢聆听!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
