2021-2022学年北师大版八年级数学下册 1.1.4等腰三角形课件 (共26张PPT)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学下册 1.1.4等腰三角形课件 (共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-27 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
北师大版数学八年级(下)
课题:等腰三角形(4)
学 习 目 标
1 掌握等边三角形的判定定理,并能加以运用.
2 掌握“30°的角所对的直角边等于斜边的一半”这一定理,并能运用定理解决问题.
3 进一步丰富探索几何图形性质的经验,提升几何推理证明的能力.
情景导入
等边三角形有哪些性质?
等边三角形的性质:
(1)等边三角形的三边都相等;
(2)等边三角形的三个内角都相等,并且每个角都等于60°;
(3)等边三角形是轴对称图形,它有三条对称轴,分别为三边的垂直平分线;
(4)各边上的高、中线、对应的角平分线重合,且长度相等.
课堂活动
等边三角形的判定
知识点一
A
B
C
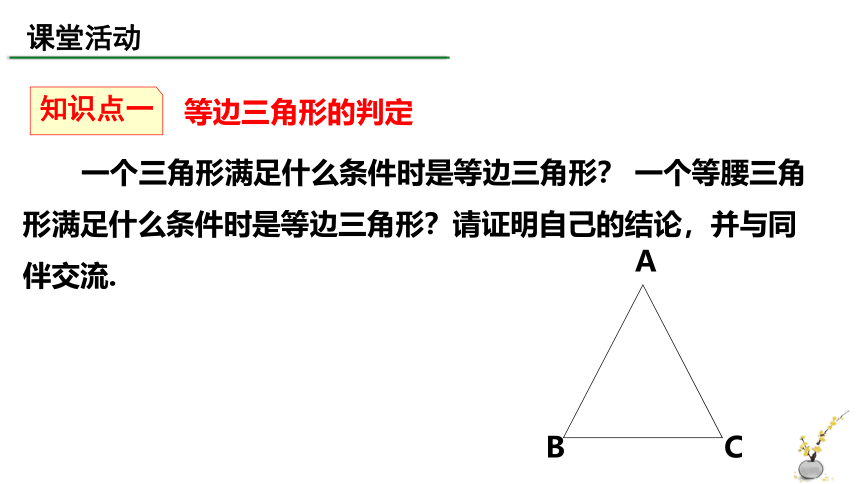
一个三角形满足什么条件时是等边三角形? 一个等腰三角形满足什么条件时是等边三角形?请证明自己的结论,并与同伴交流.
1.定义:三条边都相等的三角形是等边三角形.
如何判断它是等边三角形呢?
等边三角形的性质:三个内角都相等,每个角都是60°.
三个角都相等
等边三角形的判定: 的三角形是等边三角形.
猜想
?
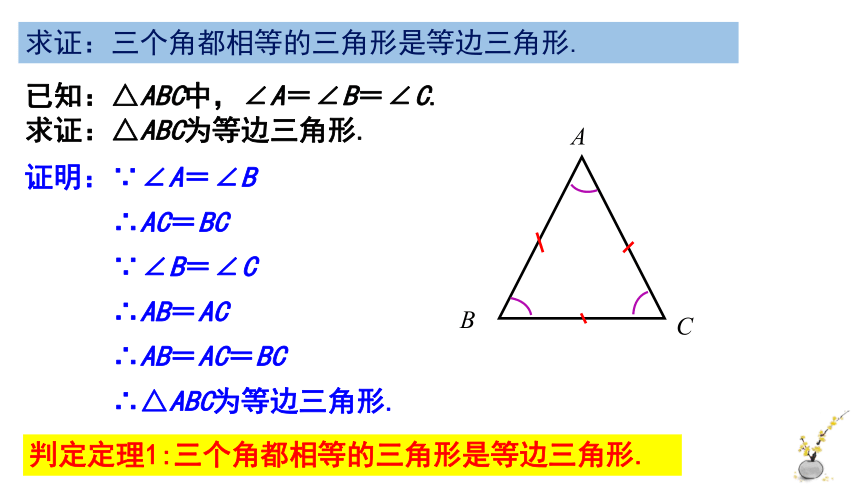
求证:三个角都相等的三角形是等边三角形.
B
C
A
已知:△ABC中,∠A=∠B=∠C.
求证:△ABC为等边三角形.
证明:∵∠A=∠B
∴AC=BC
∵∠B=∠C
∴AB=AC
∴AB=AC=BC
∴△ABC为等边三角形.
判定定理1:三个角都相等的三角形是等边三角形.
1.定义:三条边都相等的三角形是等边三角形.
有一个角是60°
等边三角形的判定: 的等腰三角形是等边三角形.
猜想
2.判定定理1:三个角都相等的三角形是等边三角形.
等边三角形是特殊的等腰三角形。
?
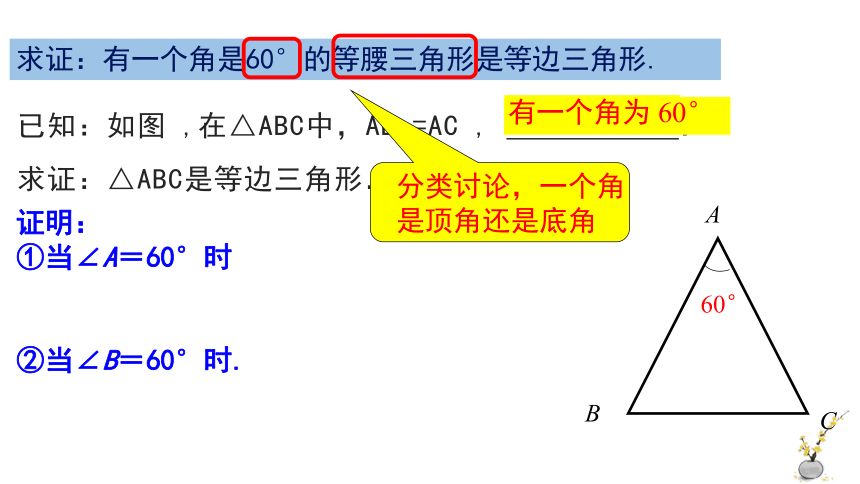
已知:如图 ,在△ABC中,AB =AC , .
求证:△ABC是等边三角形.
求证:有一个角是60°的等腰三角形是等边三角形.
B
C
A
∠A= 60°
60°
分类讨论,一个角是顶角还是底角
有一个角为 60°
证明:
①当∠A=60°时
②当∠B=60°时.
已知:如图 ,在△ABC中,AB =AC , .
求证:△ABC是等边三角形.
B
C
A
∵AB=AC
∴∠B=∠C
∵在△ABC中,∠A= 60 °
∴∠B=∠C= (180。-∠A) = 60°
∴∠A= ∠ B =∠C.
∴△ABC是等边三角形
60°
有一个角为 60°
60°
60°
证明:①当∠A=60°时
求证:有一个角是60°的等腰三角形是等边三角形.
②当∠B=60°时.
已知:如图 ,在△ABC中,AB =AC , .
求证:△ABC是等边三角形.
总结:涉及到等腰三角形,不论是边还是角,大家要有分类讨论的意识
有一个角为 60°
判定定理2:有一个角是60°的等腰三角形是等边三角形.
∵AB=AC , ∠B=60°
∴∠C=∠B=60°
∴∠A=180°-∠C-∠B=60°
∴∠A=∠B =∠C=60°.
∴△ABC是等边三角形
B
C
A
60°
60°
60°
判定定理1:三个角都相等的三角形是等边三角形.
符号语言:
∵在△ABC 中, ∠A=∠B =∠C =60°,
∴△ABC 是等边三角形.
判定定理2:有一个角为60°的等腰三角形是等边三角形
符号语言:
∵在△ABC 中,BC =AC,∠A =60°,
∴△ABC 是等边三角形.
定义法:三边相等的三角形是等边三角形.
等边三角形的判定方法
C
A
B
例1 已知:如图,△ABC 是等边三角形,与 BC 平行的直线分别交 AB 和 AC 于点 D,E.
求证:△ADE 是等边三角形.
A
B
C
D
E
典例分析
证明:∵△ABC 是等边三角形,
∴∠A =∠B =∠C = 60°,
又∵DE∥BC,
∴∠ADE =∠B = 60°,
∠AED = ∠C = 60°,
∴∠ADE =∠AED =∠A= 60°,
∴△ADE是等边三角形.
含30°角的直角三角形的性质
知识点二
做一做
用两个含30°角的全等的三角尺,你能拼成一个怎样的三角形?能拼出一个等边三角形吗?由此你能发现什么结论?说说你的理由.
定理: 在直角三角形中, 30°角所对的直角边等于
斜边的一半.
已知:在△ABC中,∠ACB=90°,∠A=30°,求证:BC= AB.
A
30°
B
C
30°
30°
A
B
D
300
A
B
C
D
∵ ∠ACB=900,∴∠ACD=900
在△ABC与△ADC中
BC=DC(作图)
∠ACB=∠ACD(已证)
AC=AC(公共边)
∴△ABC≌△ADC(SAS)
∴ AD=AB
∵∠ACB=900,∠A=300∴∠B=600
∴△ABD是等边三角形
(有一个角是600的等腰三角形是等边三角形)
∴BC= BD= AB
证明: 延长BC至D,使CD=BC,连接AD
D
B
C
A
证明:在△ACB 内部∠ACD=∠A=30°,交 AB于D
∴AD=CD ∠DCB=∠B=60°
∴△ADC是等腰三角形
(有两个角相等的三角形是等腰三角形)
又∵ ∠B=60°
∴△BCD是等边三角形
(有一个角是600的等腰三角形是等边三角形)
∴CD=BD=BC
∴BC=AD=BD
A
B
C
几何语言:
∵在Rt△ABC中,∠ACB=90°,∠A=30°
∴ BC = AB
30°
2
4
?
5
10
?
?
定理: 在直角三角形中, 30°角所对的直角边等于
斜边的一半.
典例分析
例2:求证:如果等腰三角形的底角为 15°,那么腰上的高是腰长的一半.
已知:如图,在△ABC 中,AB = AC,∠B = 15°.CD 是腰 AB 上的高. 求证:CD = AB.
1
2
证明:在△ABC 中,
∵AB = AC,∠B = 15°,
∴∠ACB =∠B = 15°(等边对等角).
∴∠DAC =∠B +∠ACB = 15°+ 15°= 30°.
∵CD 是腰 AB 上的高,
∴∠ADC = 90°.
∴CD = AC
∴CD= AB.
1
2
1
2
例3: 已知:如图,在△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于D.求证 : BD = AB
D
A
C
B
30°
证明:
∵在△ABC中
∠ACB=90°,∠A=30°
∴BC= AB ,∠B=60°
∵CD⊥AB
∴∠CDB=90°,∠BCD=30°
∴BD= BC
∴BD= AB
30°
随堂测验
1 如图,AC=BC=10 cm,∠B=15°,AD⊥BC交BC的延长线于点D,则AD的长为( )
A.3 cm
B.4 cm
C.5 cm
D.6 cm
2.如图,在△ABC 中,∠C =90°,∠A = 30°,AB =10,则BC 的长为 .
3.如图,在△ABC 中,∠ACB =90°,CD是高,∠A =30°,AB =4.则BD = .
A
B
C
300
5
A
C
B
D
1
4.如图,在△ABC中,∠B=60°,D是BC延长线上一点,过D作DE⊥AB于E,交AC于F,若CD=CF。
求证:△ABC是等边三角形
证明:∵DE⊥AB
∴∠BED=∠AEF=90°
∴∠B+∠D=90°,∠A+∠AFE=90°
∵CD=CF
∴∠D=∠DFC
∵∠DFC=∠AFE
∴∠D=∠AFE
∴∠A=∠B
∴AC=BC(等角对等边)
∵∠B=60°
∴△ABC是等边三角形
能力提升
5.如图,在△ABC中,AB=AC,D、E是△ABC内的两点,AD平∠BAC,∠EBC=∠E=60°.若BE=6cm,DE=2cm,求BC的长.
解:延长AD、ED分别交BC与M、N
M
N
∵∠EBC=∠E=60° ,∠EBC+∠E+∠BNE=180°
∴∠BNE=∠EBC=∠E=60°
∴△BEN是等边三角形
∴BE=BN=EN=6cm。
∵AB=AC,AD平分∠BAC,
∴BM=CM,AM⊥BC
∴∠DMN=90°,
∴∠MDN=30°,
∴MN= DN= (EN-DE)= (6-2)=2
∴BM=CM=BN-MN=6-2=4
∴BC=BM+CM=4+4=8
6如图,△ABC为等边三角形,点D为BC边上一动点(不与点B,C重合),∠DAE=60°,过点B作BE∥AC交AE于点E.
(1)求证:△ADE是等边三角形;
(2)当点D在何处时,AE⊥BE?指出点D的位置,并说明理由.
能力提升
等边三角形的判定方法:
定理 :三个角都相等的三角形是等边三角形.
定理 :有一个角等于60°的等腰三角形是等边三角形.
(2) 含30°角的直角三角形的性质:
在直角三角形中,如果一个锐角等于30°,那么它所对
的直角边等于斜边的一半.
课堂小结
感谢聆听!
北师大版数学八年级(下)
课题:等腰三角形(4)
学 习 目 标
1 掌握等边三角形的判定定理,并能加以运用.
2 掌握“30°的角所对的直角边等于斜边的一半”这一定理,并能运用定理解决问题.
3 进一步丰富探索几何图形性质的经验,提升几何推理证明的能力.
情景导入
等边三角形有哪些性质?
等边三角形的性质:
(1)等边三角形的三边都相等;
(2)等边三角形的三个内角都相等,并且每个角都等于60°;
(3)等边三角形是轴对称图形,它有三条对称轴,分别为三边的垂直平分线;
(4)各边上的高、中线、对应的角平分线重合,且长度相等.
课堂活动
等边三角形的判定
知识点一
A
B
C
一个三角形满足什么条件时是等边三角形? 一个等腰三角形满足什么条件时是等边三角形?请证明自己的结论,并与同伴交流.
1.定义:三条边都相等的三角形是等边三角形.
如何判断它是等边三角形呢?
等边三角形的性质:三个内角都相等,每个角都是60°.
三个角都相等
等边三角形的判定: 的三角形是等边三角形.
猜想
?
求证:三个角都相等的三角形是等边三角形.
B
C
A
已知:△ABC中,∠A=∠B=∠C.
求证:△ABC为等边三角形.
证明:∵∠A=∠B
∴AC=BC
∵∠B=∠C
∴AB=AC
∴AB=AC=BC
∴△ABC为等边三角形.
判定定理1:三个角都相等的三角形是等边三角形.
1.定义:三条边都相等的三角形是等边三角形.
有一个角是60°
等边三角形的判定: 的等腰三角形是等边三角形.
猜想
2.判定定理1:三个角都相等的三角形是等边三角形.
等边三角形是特殊的等腰三角形。
?
已知:如图 ,在△ABC中,AB =AC , .
求证:△ABC是等边三角形.
求证:有一个角是60°的等腰三角形是等边三角形.
B
C
A
∠A= 60°
60°
分类讨论,一个角是顶角还是底角
有一个角为 60°
证明:
①当∠A=60°时
②当∠B=60°时.
已知:如图 ,在△ABC中,AB =AC , .
求证:△ABC是等边三角形.
B
C
A
∵AB=AC
∴∠B=∠C
∵在△ABC中,∠A= 60 °
∴∠B=∠C= (180。-∠A) = 60°
∴∠A= ∠ B =∠C.
∴△ABC是等边三角形
60°
有一个角为 60°
60°
60°
证明:①当∠A=60°时
求证:有一个角是60°的等腰三角形是等边三角形.
②当∠B=60°时.
已知:如图 ,在△ABC中,AB =AC , .
求证:△ABC是等边三角形.
总结:涉及到等腰三角形,不论是边还是角,大家要有分类讨论的意识
有一个角为 60°
判定定理2:有一个角是60°的等腰三角形是等边三角形.
∵AB=AC , ∠B=60°
∴∠C=∠B=60°
∴∠A=180°-∠C-∠B=60°
∴∠A=∠B =∠C=60°.
∴△ABC是等边三角形
B
C
A
60°
60°
60°
判定定理1:三个角都相等的三角形是等边三角形.
符号语言:
∵在△ABC 中, ∠A=∠B =∠C =60°,
∴△ABC 是等边三角形.
判定定理2:有一个角为60°的等腰三角形是等边三角形
符号语言:
∵在△ABC 中,BC =AC,∠A =60°,
∴△ABC 是等边三角形.
定义法:三边相等的三角形是等边三角形.
等边三角形的判定方法
C
A
B
例1 已知:如图,△ABC 是等边三角形,与 BC 平行的直线分别交 AB 和 AC 于点 D,E.
求证:△ADE 是等边三角形.
A
B
C
D
E
典例分析
证明:∵△ABC 是等边三角形,
∴∠A =∠B =∠C = 60°,
又∵DE∥BC,
∴∠ADE =∠B = 60°,
∠AED = ∠C = 60°,
∴∠ADE =∠AED =∠A= 60°,
∴△ADE是等边三角形.
含30°角的直角三角形的性质
知识点二
做一做
用两个含30°角的全等的三角尺,你能拼成一个怎样的三角形?能拼出一个等边三角形吗?由此你能发现什么结论?说说你的理由.
定理: 在直角三角形中, 30°角所对的直角边等于
斜边的一半.
已知:在△ABC中,∠ACB=90°,∠A=30°,求证:BC= AB.
A
30°
B
C
30°
30°
A
B
D
300
A
B
C
D
∵ ∠ACB=900,∴∠ACD=900
在△ABC与△ADC中
BC=DC(作图)
∠ACB=∠ACD(已证)
AC=AC(公共边)
∴△ABC≌△ADC(SAS)
∴ AD=AB
∵∠ACB=900,∠A=300∴∠B=600
∴△ABD是等边三角形
(有一个角是600的等腰三角形是等边三角形)
∴BC= BD= AB
证明: 延长BC至D,使CD=BC,连接AD
D
B
C
A
证明:在△ACB 内部∠ACD=∠A=30°,交 AB于D
∴AD=CD ∠DCB=∠B=60°
∴△ADC是等腰三角形
(有两个角相等的三角形是等腰三角形)
又∵ ∠B=60°
∴△BCD是等边三角形
(有一个角是600的等腰三角形是等边三角形)
∴CD=BD=BC
∴BC=AD=BD
A
B
C
几何语言:
∵在Rt△ABC中,∠ACB=90°,∠A=30°
∴ BC = AB
30°
2
4
?
5
10
?
?
定理: 在直角三角形中, 30°角所对的直角边等于
斜边的一半.
典例分析
例2:求证:如果等腰三角形的底角为 15°,那么腰上的高是腰长的一半.
已知:如图,在△ABC 中,AB = AC,∠B = 15°.CD 是腰 AB 上的高. 求证:CD = AB.
1
2
证明:在△ABC 中,
∵AB = AC,∠B = 15°,
∴∠ACB =∠B = 15°(等边对等角).
∴∠DAC =∠B +∠ACB = 15°+ 15°= 30°.
∵CD 是腰 AB 上的高,
∴∠ADC = 90°.
∴CD = AC
∴CD= AB.
1
2
1
2
例3: 已知:如图,在△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于D.求证 : BD = AB
D
A
C
B
30°
证明:
∵在△ABC中
∠ACB=90°,∠A=30°
∴BC= AB ,∠B=60°
∵CD⊥AB
∴∠CDB=90°,∠BCD=30°
∴BD= BC
∴BD= AB
30°
随堂测验
1 如图,AC=BC=10 cm,∠B=15°,AD⊥BC交BC的延长线于点D,则AD的长为( )
A.3 cm
B.4 cm
C.5 cm
D.6 cm
2.如图,在△ABC 中,∠C =90°,∠A = 30°,AB =10,则BC 的长为 .
3.如图,在△ABC 中,∠ACB =90°,CD是高,∠A =30°,AB =4.则BD = .
A
B
C
300
5
A
C
B
D
1
4.如图,在△ABC中,∠B=60°,D是BC延长线上一点,过D作DE⊥AB于E,交AC于F,若CD=CF。
求证:△ABC是等边三角形
证明:∵DE⊥AB
∴∠BED=∠AEF=90°
∴∠B+∠D=90°,∠A+∠AFE=90°
∵CD=CF
∴∠D=∠DFC
∵∠DFC=∠AFE
∴∠D=∠AFE
∴∠A=∠B
∴AC=BC(等角对等边)
∵∠B=60°
∴△ABC是等边三角形
能力提升
5.如图,在△ABC中,AB=AC,D、E是△ABC内的两点,AD平∠BAC,∠EBC=∠E=60°.若BE=6cm,DE=2cm,求BC的长.
解:延长AD、ED分别交BC与M、N
M
N
∵∠EBC=∠E=60° ,∠EBC+∠E+∠BNE=180°
∴∠BNE=∠EBC=∠E=60°
∴△BEN是等边三角形
∴BE=BN=EN=6cm。
∵AB=AC,AD平分∠BAC,
∴BM=CM,AM⊥BC
∴∠DMN=90°,
∴∠MDN=30°,
∴MN= DN= (EN-DE)= (6-2)=2
∴BM=CM=BN-MN=6-2=4
∴BC=BM+CM=4+4=8
6如图,△ABC为等边三角形,点D为BC边上一动点(不与点B,C重合),∠DAE=60°,过点B作BE∥AC交AE于点E.
(1)求证:△ADE是等边三角形;
(2)当点D在何处时,AE⊥BE?指出点D的位置,并说明理由.
能力提升
等边三角形的判定方法:
定理 :三个角都相等的三角形是等边三角形.
定理 :有一个角等于60°的等腰三角形是等边三角形.
(2) 含30°角的直角三角形的性质:
在直角三角形中,如果一个锐角等于30°,那么它所对
的直角边等于斜边的一半.
课堂小结
感谢聆听!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
