2021-2022学年北师大版八年级数学下册 4.1因式分解课件 (共20张PPT)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学下册 4.1因式分解课件 (共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-27 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
北师大版数学八年级(下)
课题:因式分解
学 习 目 标
1.理解掌握因式分解的意义.会判断一个变形是否为因式分解.(重点)
2.通过观察,理解识别因式分解与整式乘法之间的联系与区别.(难点)
复习回顾
1、单项式:若一个代数式是_______________,这样的代数式叫作单项式,单独______ 或 ________ 也是单项式.
数与字母的乘积
一个数
一个字母
例如,
2 多项式:几个单项式的___ 叫作多项式.
例如,
3 整式:单项式和多项式统称整式.
和
复习回顾
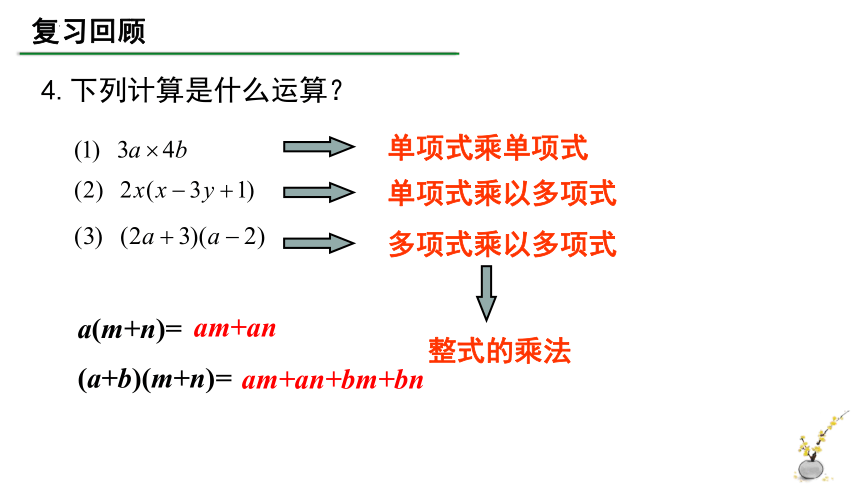
4.下列计算是什么运算?
单项式乘单项式
单项式乘以多项式
多项式乘以多项式
整式的乘法
a(m+n)=
am+an
(a+b)(m+n)=
am+an+bm+bn
复习回顾
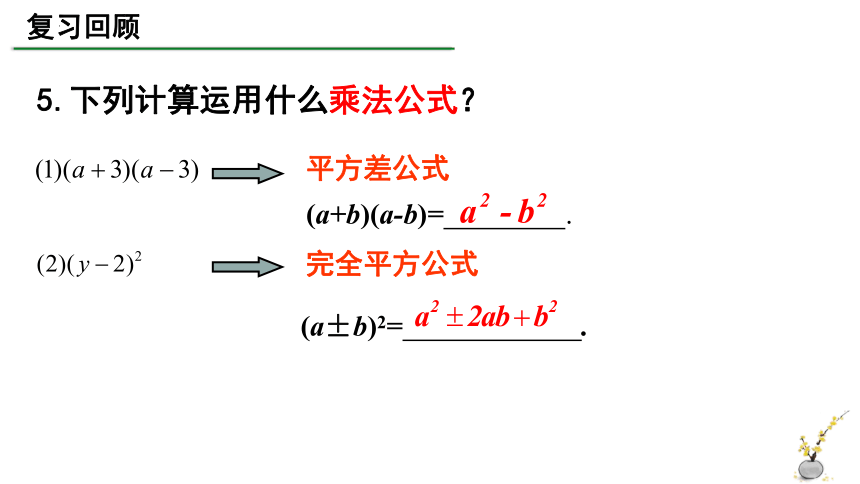
5.下列计算运用什么乘法公式?
平方差公式
完全平方公式
(a+b)(a-b)= .
(a±b)2= .
想一想: 993-99还能被哪些整数整除
探究:993-99能被100整除吗 你是怎样想的
你能尝试把 化成几个整式的乘积的形式吗?
深入理解
观察下面的拼图过程,写出相应的关系式
把一个多项式化成几个整式的积的形式,这种变形叫做因式分解.也可称为分解因式.
a3-a= a (a+1) (a-1)
注意:①分解的对象必须是多项式
②因式分解的结果:积的形式
③结果中的每一个因式都必须是整式
④必须分解到每个因式都不能再分解为止
t2-16+3t=(t+4)(t-4)+3t
多项式
am+bm+cm=m (a+b+c)
整式的积
多项式
整式的积
概念
Ⅰ计算下列各式:
Ⅱ根据左边算式填空:
积的形式
转化
和的形式
和的形式
转化
积的形式
整式乘法
因式分解
整式乘法与分解因式是互逆运算
典例分析
1. 下列各式由左到右的变形是因式分解的是( )
A.-9+a2=-(3+a)(3-a) B.(x-2)(x-3)=x2-x-6
C.a2-2ab+b2+a=(a-b)2+a D.m2+m=m2(1+ )
典例分析
2:若多项式x2+ax+b分解因式的结果为a(x﹣2)(x+3),求a,b的值.
解:∵x2+ax+b=a(x﹣2)(x+3)
=ax2+ax-6a.
∴a=1, b=﹣6a=﹣6.
方法归纳:对于此类问题,掌握因式分解与整式乘法为互逆运算是解题关键,应先把分解因式后的结果乘开,再与多项式的各项系数相对应比较即可.
典例分析
随堂检测
1、若2(x-m)(x+2)是多项式2x2+nx-6+n分解后的结果,求m+n的平方根.
解:2(x-m)(x+2)=2x2+(4-2m)x-4m,
因为2(x-m)(x+2)是多项式2x2+nx-6+n分解后的结果,
所以2x2+(4-2m)x-4m=2x2+nx-6+n.
4-2m=n
-4m=-6+n
{
所以
解得 m=1
n=2
{
所以m+n=2+1=3.
所以m+n的平方根是± .
随堂检测
2.若 x2+mx-n能分解成(x-3)(x-5),求m,n的值。
解:由题意得: x2+mx-n = (x-3)(x-5)
∵ x2+mx-n =x -8x+15
∴对应项的系数相等,则m= -8, m= 15
随堂检测
3. 若多项式x4+mx3+nx﹣16含有因式(x﹣2)和(x﹣1), 求mn的值.
解:∵x4+mx3+nx﹣16的最高次数是4,
∴可设x4+mx3+nx﹣16=(x-1)(x-2)(x2+ax+b),
则x4+mx3+nx-16=x4+(a-3)x3+(b-3a+2)x2+(2a-3b)x+2b
比较系数得 2b=-16,b-3a+2=0,a-3=m,2a-3b=n
解得a=-2,b=-8,m=-5,n=20.
∴mn=﹣5×20=﹣100.
能力提升
1.证明对于任何整数n,多项式(n+7)2-(n-3)2的值都能被20整除
能力提升
2.已知多项式2x2+3xy-2y2-x+8y-6可分解为(x+2y+m)(2x-y+n)的形式.试求:m、n的值.
课堂小结
你能说说什么是分解因式吗?
把一个多项式化成几个整式的积的形式叫做把这个多项式分解因式。
应该怎样认识“因式分解”
分解因式与整式乘法是互为逆运算的变形过程。
分解因式要注意到什么?
1.分解的对象必须是多项式.
2.分解的结果一定是几个整式的乘积的形式.
3.要分解到不能分解为止.
感谢聆听!
北师大版数学八年级(下)
课题:因式分解
学 习 目 标
1.理解掌握因式分解的意义.会判断一个变形是否为因式分解.(重点)
2.通过观察,理解识别因式分解与整式乘法之间的联系与区别.(难点)
复习回顾
1、单项式:若一个代数式是_______________,这样的代数式叫作单项式,单独______ 或 ________ 也是单项式.
数与字母的乘积
一个数
一个字母
例如,
2 多项式:几个单项式的___ 叫作多项式.
例如,
3 整式:单项式和多项式统称整式.
和
复习回顾
4.下列计算是什么运算?
单项式乘单项式
单项式乘以多项式
多项式乘以多项式
整式的乘法
a(m+n)=
am+an
(a+b)(m+n)=
am+an+bm+bn
复习回顾
5.下列计算运用什么乘法公式?
平方差公式
完全平方公式
(a+b)(a-b)= .
(a±b)2= .
想一想: 993-99还能被哪些整数整除
探究:993-99能被100整除吗 你是怎样想的
你能尝试把 化成几个整式的乘积的形式吗?
深入理解
观察下面的拼图过程,写出相应的关系式
把一个多项式化成几个整式的积的形式,这种变形叫做因式分解.也可称为分解因式.
a3-a= a (a+1) (a-1)
注意:①分解的对象必须是多项式
②因式分解的结果:积的形式
③结果中的每一个因式都必须是整式
④必须分解到每个因式都不能再分解为止
t2-16+3t=(t+4)(t-4)+3t
多项式
am+bm+cm=m (a+b+c)
整式的积
多项式
整式的积
概念
Ⅰ计算下列各式:
Ⅱ根据左边算式填空:
积的形式
转化
和的形式
和的形式
转化
积的形式
整式乘法
因式分解
整式乘法与分解因式是互逆运算
典例分析
1. 下列各式由左到右的变形是因式分解的是( )
A.-9+a2=-(3+a)(3-a) B.(x-2)(x-3)=x2-x-6
C.a2-2ab+b2+a=(a-b)2+a D.m2+m=m2(1+ )
典例分析
2:若多项式x2+ax+b分解因式的结果为a(x﹣2)(x+3),求a,b的值.
解:∵x2+ax+b=a(x﹣2)(x+3)
=ax2+ax-6a.
∴a=1, b=﹣6a=﹣6.
方法归纳:对于此类问题,掌握因式分解与整式乘法为互逆运算是解题关键,应先把分解因式后的结果乘开,再与多项式的各项系数相对应比较即可.
典例分析
随堂检测
1、若2(x-m)(x+2)是多项式2x2+nx-6+n分解后的结果,求m+n的平方根.
解:2(x-m)(x+2)=2x2+(4-2m)x-4m,
因为2(x-m)(x+2)是多项式2x2+nx-6+n分解后的结果,
所以2x2+(4-2m)x-4m=2x2+nx-6+n.
4-2m=n
-4m=-6+n
{
所以
解得 m=1
n=2
{
所以m+n=2+1=3.
所以m+n的平方根是± .
随堂检测
2.若 x2+mx-n能分解成(x-3)(x-5),求m,n的值。
解:由题意得: x2+mx-n = (x-3)(x-5)
∵ x2+mx-n =x -8x+15
∴对应项的系数相等,则m= -8, m= 15
随堂检测
3. 若多项式x4+mx3+nx﹣16含有因式(x﹣2)和(x﹣1), 求mn的值.
解:∵x4+mx3+nx﹣16的最高次数是4,
∴可设x4+mx3+nx﹣16=(x-1)(x-2)(x2+ax+b),
则x4+mx3+nx-16=x4+(a-3)x3+(b-3a+2)x2+(2a-3b)x+2b
比较系数得 2b=-16,b-3a+2=0,a-3=m,2a-3b=n
解得a=-2,b=-8,m=-5,n=20.
∴mn=﹣5×20=﹣100.
能力提升
1.证明对于任何整数n,多项式(n+7)2-(n-3)2的值都能被20整除
能力提升
2.已知多项式2x2+3xy-2y2-x+8y-6可分解为(x+2y+m)(2x-y+n)的形式.试求:m、n的值.
课堂小结
你能说说什么是分解因式吗?
把一个多项式化成几个整式的积的形式叫做把这个多项式分解因式。
应该怎样认识“因式分解”
分解因式与整式乘法是互为逆运算的变形过程。
分解因式要注意到什么?
1.分解的对象必须是多项式.
2.分解的结果一定是几个整式的乘积的形式.
3.要分解到不能分解为止.
感谢聆听!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
