2021-2022学年冀教版八年级数学下学期22.1平行四边形的性质 课件 (共30张PPT)
文档属性
| 名称 | 2021-2022学年冀教版八年级数学下学期22.1平行四边形的性质 课件 (共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 9.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-27 00:00:00 | ||
图片预览





文档简介
(共30张PPT)
第二十二章 四边形
22.1平形四边形的性质(1)
温故而知新
温故而知新
温故而知新
温故而知新
温故而知新
温故而知新
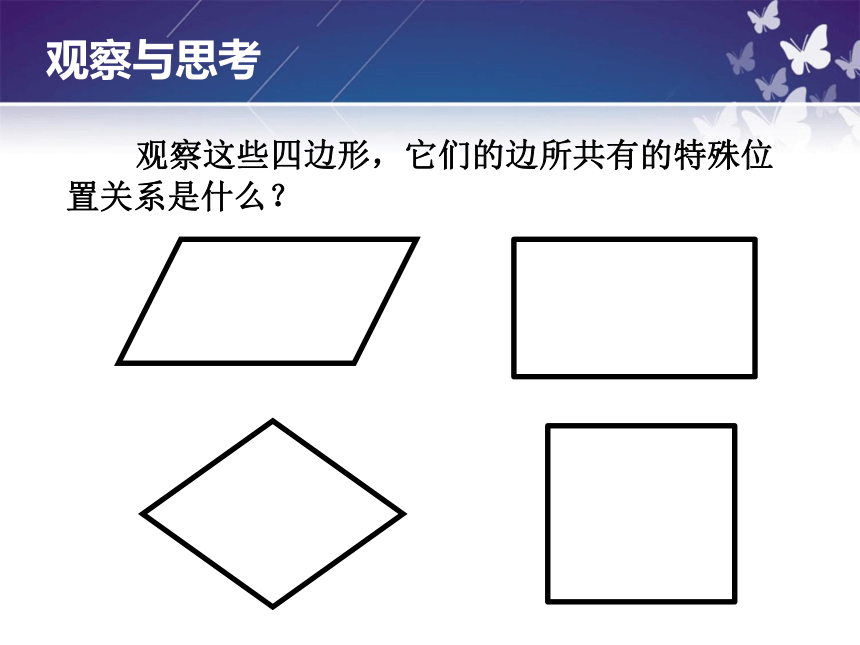
观察这些四边形,它们的边所共有的特殊位置关系是什么?
观察与思考
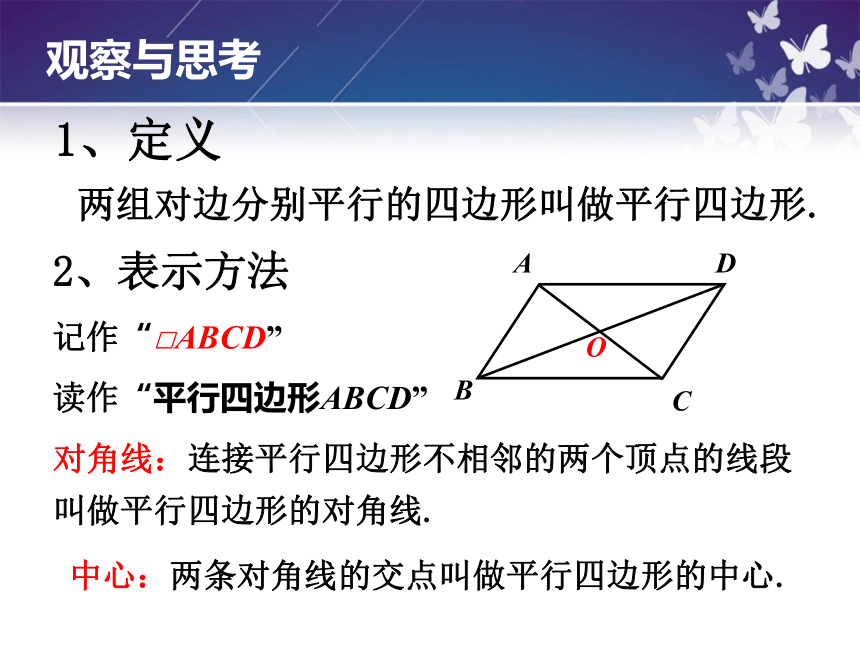
1、定义
两组对边分别平行的四边形叫做平行四边形.
A
B
C
D
O
记作“□ABCD”
读作“平行四边形ABCD”
2、表示方法
对角线:连接平行四边形不相邻的两个顶点的线段叫做平行四边形的对角线.
中心:两条对角线的交点叫做平行四边形的中心.
观察与思考
A
B
C
D
∵四边形ABCD是平行四边形
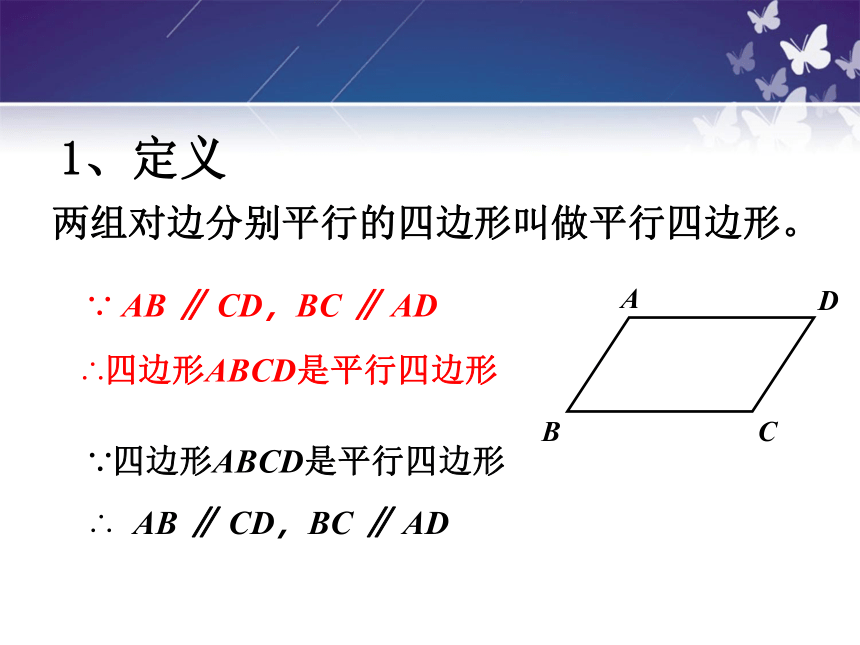
1、定义
两组对边分别平行的四边形叫做平行四边形。
∵ AB ∥ CD,BC ∥ AD
∴四边形ABCD是平行四边形
∴ AB ∥ CD,BC ∥ AD
两张有一组对边平行的纸片,随意交叉叠放在一起,重合部分构成了一个四边形,这个四边形是不是平行四边形,为什么
操作与探究
两张有一组对边平行的纸片,随意交叉叠放在一起,重合部分构成了一个四边形,这个四边形是不是平行四边形,为什么
操作与探究
请你用两张有一组对边平行的纸片,随意交叉叠放在一起,剪出两个完全一样的平行四边形纸片.
①
②
③
④
观察平行四边形纸片.请你探究平行四边形的对称性.
1、平行四边形是轴对称图形吗?为什么?
2、平行四边形是中心对称图形吗?为什么?
操作与探究
平行四边形是中心对称图形,对称中心是两条对角线的交点.
探究过程中,你发现构成平行四边形的边、角、对角线有什么特征呢?
●
A
D
O
C
B
D
B
O
C
A
操作与探究
已知: 如右图, 四边形ABCD是平行四边形.
求证:(1)AB=CD, AD=CB;
(2)∠BAD=∠DCB,∠ABC=∠CDA.
A
B
C
D
操作与探究
证明平行四边形的对边相等、对角相等.
已知:如图所示,四边形ABCD是平行四边形.
求证:(1)AD=CB,AB=CD.
(2)∠BAD=∠DCB,∠ABC=∠CDA.
证明:如图所示,连接BD,在△ABD和△CDB中,
∵AD∥CB,AB∥CD,
∴∠ABD=∠CDB,∠ADB=∠CBD.
又∵BD=DB,
∴△ABD≌△CDB.
∴AD=CB,AB=CD,∠BAD=∠DCB.
∵∠ABD=∠CDB,∠ADB=∠CBD,
∴∠ABD+∠CBD=∠CDB+∠ADB,
即∠ABC=∠CDA.
平行四边形的性质定理:平行四边形的对边相等,对角相等.
平行四边形的性质定理:
平行四边形的对边相等, 对角相等.
A
B
C
D
∵四边形ABCD是平行四边形
∴AB=CD, AD=CB
∠BAD=∠DCB, ∠ABC=∠CDA.
或:在□ABCD中,AB=CD, AD=CB
∠BAD=∠DCB,∠ABC=∠CDA.
符号语言
回忆小学研究平行四边形性质的方法,与今
天的研究方法进行对比,有什么不同?
量一量
对折
操作与探究
已知:如图所示, □ ABCD的周长为22 cm,△ABD的周长为18 cm,求对角线BD的长.
解:∵四边形ABCD是平行四边形,
∴AD=BC , AB=DC.
∵ □ ABCD的周长为22 cm,
∴ 2(AB+AD)=22, ∴AB+AD=11.
又∵ △ABD的周长为18 cm ,即AB+AD+BD=18,
∴BD=18-11=7.
实践与应用
(教材第118页例1) 已知:如图所示,在□ ABCD中,∠B+∠D=260°,求∠A,∠C的度数.
解:在□ ABCD中,
∵∠B=∠D,∠B+∠D=260°,
∴∠B=∠D =130°.
又∵AD∥CB,
∴∠A=180°-∠B=180°-130°=50°.
∴∠C=∠A=50°.
操作与探究
A
B
C
D
O
感悟与收获
感悟与收获
感谢您的倾听!
1.如图所示,在平行四边形ABCD中,对角线AC,BD相交于点O,图中的全等三角形的对数为 ( )
A.1对 B.2对 C.3对 D.4对
解析:∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,OD=OB,OA=OC.在△AOD和△COB中,
∴△AOD≌△COB(SAS).同理可得△AOB≌△COD(SAS).在△ABD和△CDB中,
∴△ABD≌△CDB(SSS).同理可得△ACD≌△CAB(SSS).共有4对全等三角形.故选D.
D
检测反馈
2.如图所示, ABCD中,AE平分∠BAD,若CE=3 cm,AB=4 cm,则 ABCD的周长是 ( )
A.20 cm B.21 cm C.22 cm D.23 cm
解析:∵四边形ABCD是平行四边形,∴AD=BC,AB=DC,AD∥BC,∴∠DAE=∠BEA.∵AE平分∠BAD,∴∠BAE=∠DAE,∴∠BEA=∠BAE,∴BE=AB=4 cm,∴BC=BE+CE=7 cm,∴ ABCD的周长=2(AB+BC)=2(4+7)=22(cm).故选C.
C
3.在 ABCD中,若∠B=4∠A,则∠D等于 ( )
A.18° B.36° C.72° D.144°
解析:∵四边形ABCD是平行四边形,∴AD∥CB,∠B=∠D,∴∠A+∠B=180°.∵∠B=4∠A,∴∠A+4∠A=180°,解得∠A=36°,∴∠B=144°,∴∠D=144°.故选D.
D
4.如图所示,在 ABCD中,下列结论一定正确的是 ( )
①∠1+∠2=180°;
②∠2+∠3=180°;
③∠3+∠4=180°;
④∠2+∠4=180°.
A.①②③ B.②③④
C.①②④ D.①③④
解析:∵∠1和∠2是邻补角,∴∠1+∠2=180°.∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,∴∠2=∠4,∠2+∠3=180°,∠3+∠4=180°,∴正确的有①②③.故选A.
A
5.(2016·孝感中考)在 ABCD中,AD=8,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,且EF=2,则AB的长为 ( )
A.3 B.5 C.2或3 D.3或5
图(1)
图(2)
解析:第一种情况:如图(1)所示,在 ABCD中,∵BC=AD=8,BC∥AD,CD=AB,CD∥AB,∴∠DAE=∠AEB,∠ADF=∠DFC.∵AE平分∠BAD,DF平分∠ADC,∴∠BAE=∠DAE,∠ADF=∠CDF,∴∠BAE=∠AEB,∠CFD=∠CDF,∴AB=BE,CF=CD.∵EF=2,∴BC=BE+EF+CF=2AB+EF=8,∴AB=3.
第二种情况:如图(2)所示,在 ABCD中,∵BC=AD=8,BC∥AD,CD=AB,CD∥AB,∴∠DAE=∠AEB,∠ADF=∠DFC,∵AE平分∠BAD,DF平分∠ADC,∴∠BAE=∠DAE,∠ADF=∠CDF,∴∠BAE=∠AEB,∠CFD=∠CDF,∴AB=BE,CF=CD.∵EF=2,∴BC=BE+CF-EF=2AB-EF=8,∴AB=5.
综上,AB的长为3或5.故选D.
D
6.一个平行四边形的周长为70 cm,相邻两边长度的差是5 cm,则这个平行四边形较长边的长为 cm.
解析:设该平行四边形的两边长分别为x cm,y cm,且x>y,根据题意,得 解得 则这个平行四边形较长边的长为20 cm.故填20.
20
7.用40 cm长的绳子围成一个平行四边形,使其相邻两边的长度比为3∶2,则较长边的长为 cm.
解析:设较长边的长为3x cm,则另一边的长为2x cm.根据题意,得2(2x+3x)=40,解得x=4,∴较长边的长为3×4=12(cm).故填12.
12
8.如图所示,在 ABCD中,E是CD的中点,AE的延长线与BC的延长线相交于点F.
求证BC=CF.
解析:先证明△ADE≌△FCE,得出AD=CF,再根据平行四边形的性质可知AD=BC,继而得出结论.
证明:∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC.
∴∠ADE=∠FCE.
∵E是CD的中点,∴DE=CE.
在△ADE和△FCE中,
∴△ADE≌△FCE,∴AD=CF.
∴BC=CF.
第二十二章 四边形
22.1平形四边形的性质(1)
温故而知新
温故而知新
温故而知新
温故而知新
温故而知新
温故而知新
观察这些四边形,它们的边所共有的特殊位置关系是什么?
观察与思考
1、定义
两组对边分别平行的四边形叫做平行四边形.
A
B
C
D
O
记作“□ABCD”
读作“平行四边形ABCD”
2、表示方法
对角线:连接平行四边形不相邻的两个顶点的线段叫做平行四边形的对角线.
中心:两条对角线的交点叫做平行四边形的中心.
观察与思考
A
B
C
D
∵四边形ABCD是平行四边形
1、定义
两组对边分别平行的四边形叫做平行四边形。
∵ AB ∥ CD,BC ∥ AD
∴四边形ABCD是平行四边形
∴ AB ∥ CD,BC ∥ AD
两张有一组对边平行的纸片,随意交叉叠放在一起,重合部分构成了一个四边形,这个四边形是不是平行四边形,为什么
操作与探究
两张有一组对边平行的纸片,随意交叉叠放在一起,重合部分构成了一个四边形,这个四边形是不是平行四边形,为什么
操作与探究
请你用两张有一组对边平行的纸片,随意交叉叠放在一起,剪出两个完全一样的平行四边形纸片.
①
②
③
④
观察平行四边形纸片.请你探究平行四边形的对称性.
1、平行四边形是轴对称图形吗?为什么?
2、平行四边形是中心对称图形吗?为什么?
操作与探究
平行四边形是中心对称图形,对称中心是两条对角线的交点.
探究过程中,你发现构成平行四边形的边、角、对角线有什么特征呢?
●
A
D
O
C
B
D
B
O
C
A
操作与探究
已知: 如右图, 四边形ABCD是平行四边形.
求证:(1)AB=CD, AD=CB;
(2)∠BAD=∠DCB,∠ABC=∠CDA.
A
B
C
D
操作与探究
证明平行四边形的对边相等、对角相等.
已知:如图所示,四边形ABCD是平行四边形.
求证:(1)AD=CB,AB=CD.
(2)∠BAD=∠DCB,∠ABC=∠CDA.
证明:如图所示,连接BD,在△ABD和△CDB中,
∵AD∥CB,AB∥CD,
∴∠ABD=∠CDB,∠ADB=∠CBD.
又∵BD=DB,
∴△ABD≌△CDB.
∴AD=CB,AB=CD,∠BAD=∠DCB.
∵∠ABD=∠CDB,∠ADB=∠CBD,
∴∠ABD+∠CBD=∠CDB+∠ADB,
即∠ABC=∠CDA.
平行四边形的性质定理:平行四边形的对边相等,对角相等.
平行四边形的性质定理:
平行四边形的对边相等, 对角相等.
A
B
C
D
∵四边形ABCD是平行四边形
∴AB=CD, AD=CB
∠BAD=∠DCB, ∠ABC=∠CDA.
或:在□ABCD中,AB=CD, AD=CB
∠BAD=∠DCB,∠ABC=∠CDA.
符号语言
回忆小学研究平行四边形性质的方法,与今
天的研究方法进行对比,有什么不同?
量一量
对折
操作与探究
已知:如图所示, □ ABCD的周长为22 cm,△ABD的周长为18 cm,求对角线BD的长.
解:∵四边形ABCD是平行四边形,
∴AD=BC , AB=DC.
∵ □ ABCD的周长为22 cm,
∴ 2(AB+AD)=22, ∴AB+AD=11.
又∵ △ABD的周长为18 cm ,即AB+AD+BD=18,
∴BD=18-11=7.
实践与应用
(教材第118页例1) 已知:如图所示,在□ ABCD中,∠B+∠D=260°,求∠A,∠C的度数.
解:在□ ABCD中,
∵∠B=∠D,∠B+∠D=260°,
∴∠B=∠D =130°.
又∵AD∥CB,
∴∠A=180°-∠B=180°-130°=50°.
∴∠C=∠A=50°.
操作与探究
A
B
C
D
O
感悟与收获
感悟与收获
感谢您的倾听!
1.如图所示,在平行四边形ABCD中,对角线AC,BD相交于点O,图中的全等三角形的对数为 ( )
A.1对 B.2对 C.3对 D.4对
解析:∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,OD=OB,OA=OC.在△AOD和△COB中,
∴△AOD≌△COB(SAS).同理可得△AOB≌△COD(SAS).在△ABD和△CDB中,
∴△ABD≌△CDB(SSS).同理可得△ACD≌△CAB(SSS).共有4对全等三角形.故选D.
D
检测反馈
2.如图所示, ABCD中,AE平分∠BAD,若CE=3 cm,AB=4 cm,则 ABCD的周长是 ( )
A.20 cm B.21 cm C.22 cm D.23 cm
解析:∵四边形ABCD是平行四边形,∴AD=BC,AB=DC,AD∥BC,∴∠DAE=∠BEA.∵AE平分∠BAD,∴∠BAE=∠DAE,∴∠BEA=∠BAE,∴BE=AB=4 cm,∴BC=BE+CE=7 cm,∴ ABCD的周长=2(AB+BC)=2(4+7)=22(cm).故选C.
C
3.在 ABCD中,若∠B=4∠A,则∠D等于 ( )
A.18° B.36° C.72° D.144°
解析:∵四边形ABCD是平行四边形,∴AD∥CB,∠B=∠D,∴∠A+∠B=180°.∵∠B=4∠A,∴∠A+4∠A=180°,解得∠A=36°,∴∠B=144°,∴∠D=144°.故选D.
D
4.如图所示,在 ABCD中,下列结论一定正确的是 ( )
①∠1+∠2=180°;
②∠2+∠3=180°;
③∠3+∠4=180°;
④∠2+∠4=180°.
A.①②③ B.②③④
C.①②④ D.①③④
解析:∵∠1和∠2是邻补角,∴∠1+∠2=180°.∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,∴∠2=∠4,∠2+∠3=180°,∠3+∠4=180°,∴正确的有①②③.故选A.
A
5.(2016·孝感中考)在 ABCD中,AD=8,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,且EF=2,则AB的长为 ( )
A.3 B.5 C.2或3 D.3或5
图(1)
图(2)
解析:第一种情况:如图(1)所示,在 ABCD中,∵BC=AD=8,BC∥AD,CD=AB,CD∥AB,∴∠DAE=∠AEB,∠ADF=∠DFC.∵AE平分∠BAD,DF平分∠ADC,∴∠BAE=∠DAE,∠ADF=∠CDF,∴∠BAE=∠AEB,∠CFD=∠CDF,∴AB=BE,CF=CD.∵EF=2,∴BC=BE+EF+CF=2AB+EF=8,∴AB=3.
第二种情况:如图(2)所示,在 ABCD中,∵BC=AD=8,BC∥AD,CD=AB,CD∥AB,∴∠DAE=∠AEB,∠ADF=∠DFC,∵AE平分∠BAD,DF平分∠ADC,∴∠BAE=∠DAE,∠ADF=∠CDF,∴∠BAE=∠AEB,∠CFD=∠CDF,∴AB=BE,CF=CD.∵EF=2,∴BC=BE+CF-EF=2AB-EF=8,∴AB=5.
综上,AB的长为3或5.故选D.
D
6.一个平行四边形的周长为70 cm,相邻两边长度的差是5 cm,则这个平行四边形较长边的长为 cm.
解析:设该平行四边形的两边长分别为x cm,y cm,且x>y,根据题意,得 解得 则这个平行四边形较长边的长为20 cm.故填20.
20
7.用40 cm长的绳子围成一个平行四边形,使其相邻两边的长度比为3∶2,则较长边的长为 cm.
解析:设较长边的长为3x cm,则另一边的长为2x cm.根据题意,得2(2x+3x)=40,解得x=4,∴较长边的长为3×4=12(cm).故填12.
12
8.如图所示,在 ABCD中,E是CD的中点,AE的延长线与BC的延长线相交于点F.
求证BC=CF.
解析:先证明△ADE≌△FCE,得出AD=CF,再根据平行四边形的性质可知AD=BC,继而得出结论.
证明:∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC.
∴∠ADE=∠FCE.
∵E是CD的中点,∴DE=CE.
在△ADE和△FCE中,
∴△ADE≌△FCE,∴AD=CF.
∴BC=CF.
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
