北师大版七年级数学下册1.4 单项式乘以多单项式课件(共20张PPT)
文档属性
| 名称 | 北师大版七年级数学下册1.4 单项式乘以多单项式课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-27 16:47:17 | ||
图片预览








文档简介
(共20张PPT)
同学们好
§1.4 整式的乘法(2)
北师版七年级下册
第一章 整式的乘除
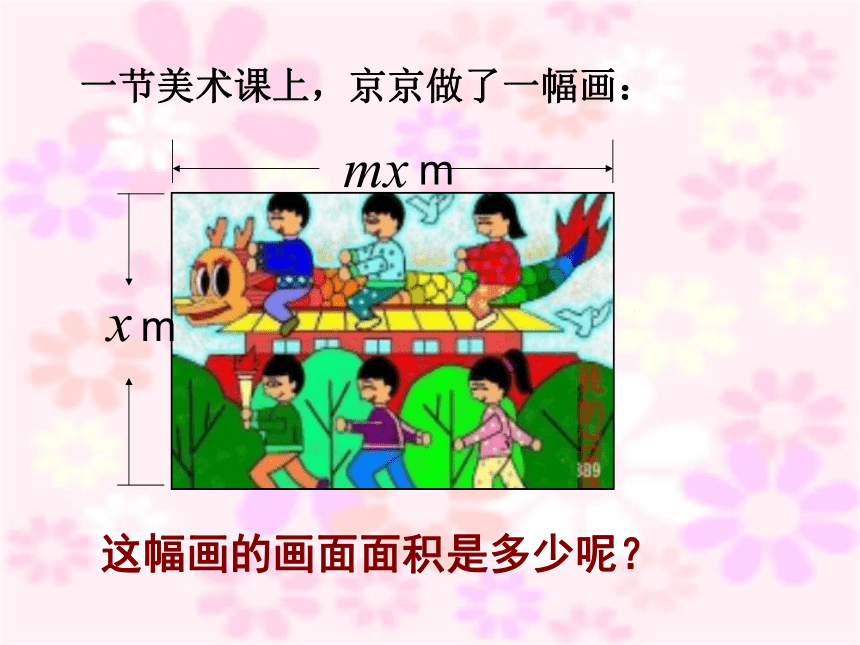
这幅画的画面面积是多少呢?
一节美术课上,京京做了一幅画:
m
m
互动探究
宁宁也作了一幅
画,所用纸的大小和
京京一样,但是他在
纸的左、右两边各留
了 米的空白,这
幅画的画面面积是多
少?
你能用两种方法得到画面面积吗?
(1)先表示出画面的
长和宽,由此得到画
面的面积是
(2)用纸的面积减去
空白处的面积,由此
得到画面的面积是
互动探究
仔细想一想
(3)由上面的探索,我们得到了:
=
—
单项式
————
多项式
你能用所学过的知识来说明上面的等式成立的原因吗
(4)你能再举一些单项式与多项式相乘的式子吗?请用上面的方法计算并说明每一步的依据。
(5)通过以上过程,你发现如何进行单项式与多项式相乘的运算?请你试着用语言来描述。
仔细想一想
认识新朋友
单项式与多项式相乘的法则
单项式与多项式相乘,就是根据分配律用单项式去乘多项式的每一项,再把所得的积相加。
m(a+b+c)= ma+mb+mc
(m,a,b,c都是单项式)
你能用字母表示这一结论吗?
应用新知
例1:计算 -2a2·(3a2-5b).
解:原式=(-2a2)· 3a2 +(-2a2)· (-5b)
=-6a4+10a2b.
方法总结:单项式与多项式相乘实质就是转化为单项式与单项式相乘.
下列计算对吗?若不对,应该怎样改?
(1)
(2)
(3)
(4)
应用新知
不要漏乘
计算仔细
注意负号
错
错
错
正确
例2 一条防洪堤坝,其横断面是梯形,上底宽a米,下底宽(a+2b)米,坝高a米.
(1)求防洪堤坝的横断面面积;
(2)如果防洪堤坝长100米,那么这段防洪堤坝的体积是多少立方米?
典例精析
典例精析
解:(1)
=
= (平方米).
故防洪堤坝的横断面面积为 平方米;
故这段防洪堤坝的体积为 (立方米).
例3 先化简,再求值:5a(2a2-5a+3)-2a2(5a+5),
其中a=2.
典例精析
(1)将2x2与5x前面的“-”看成性质符号;
(2)单项式与多项式相乘的结果中,应将同类项合并.
注意
解:5a(2a2-5a+3)-2a2(5a+5)
=10a3-25a2+15a-10a3-10a2
=-35a2+15a,
当a=2时,原式= =-110.
师生互动点评
(1)多项式每一项要包括前面的符号;
(2)单项式须与多项式中每一项相乘,
结果要化到最简;
(3)单项式系数为负时,改变多项式
每项的符号。
我来试一试
1.计算:
(1)(-4x)·(2x2+3x-1)
(2)-2x2·(xy+y2)-5x(x2y-xy2).
2.先化简,再求值:
3a(2a2-4a+3)-2a2(3a+4),其中 a=-2.
我来试一试
(1)(-4x)·(2x2+3x-1)
解:(1)原式
(2)-2x2·(xy+y2)-5x(x2y-xy2).
解:原式=( -2x2) ·xy+(-2x2) ·y2+ (-5x) ·x2y+(-5x) ·(-xy2)
=-2x3y+(-2x2y2)+(-5x3y)+5x2y2
=-7x3y+3x2y2.
2.先化简,再求值3a(2a2-4a+3)-2a2(3a+4),其中
a=-2.
解:3a(2a2-4a+3)-2a2(3a+4)
=6a3-12a2+9a-6a3-8a2
=-20a2+9a.
当a=-2时
原式=-20×(-2)2+9×(-2)
=-98.
知识梳理
通过今天的学习,用你自己的话说说你的收获和体会。
1.单项式乘以多项式的法则
2.在应用单项式乘以多项式的法则进行运算时应注意哪些问题?
3.数形结合、转化、归纳等数
学思想与方法.
再
见
同学们好
§1.4 整式的乘法(2)
北师版七年级下册
第一章 整式的乘除
这幅画的画面面积是多少呢?
一节美术课上,京京做了一幅画:
m
m
互动探究
宁宁也作了一幅
画,所用纸的大小和
京京一样,但是他在
纸的左、右两边各留
了 米的空白,这
幅画的画面面积是多
少?
你能用两种方法得到画面面积吗?
(1)先表示出画面的
长和宽,由此得到画
面的面积是
(2)用纸的面积减去
空白处的面积,由此
得到画面的面积是
互动探究
仔细想一想
(3)由上面的探索,我们得到了:
=
—
单项式
————
多项式
你能用所学过的知识来说明上面的等式成立的原因吗
(4)你能再举一些单项式与多项式相乘的式子吗?请用上面的方法计算并说明每一步的依据。
(5)通过以上过程,你发现如何进行单项式与多项式相乘的运算?请你试着用语言来描述。
仔细想一想
认识新朋友
单项式与多项式相乘的法则
单项式与多项式相乘,就是根据分配律用单项式去乘多项式的每一项,再把所得的积相加。
m(a+b+c)= ma+mb+mc
(m,a,b,c都是单项式)
你能用字母表示这一结论吗?
应用新知
例1:计算 -2a2·(3a2-5b).
解:原式=(-2a2)· 3a2 +(-2a2)· (-5b)
=-6a4+10a2b.
方法总结:单项式与多项式相乘实质就是转化为单项式与单项式相乘.
下列计算对吗?若不对,应该怎样改?
(1)
(2)
(3)
(4)
应用新知
不要漏乘
计算仔细
注意负号
错
错
错
正确
例2 一条防洪堤坝,其横断面是梯形,上底宽a米,下底宽(a+2b)米,坝高a米.
(1)求防洪堤坝的横断面面积;
(2)如果防洪堤坝长100米,那么这段防洪堤坝的体积是多少立方米?
典例精析
典例精析
解:(1)
=
= (平方米).
故防洪堤坝的横断面面积为 平方米;
故这段防洪堤坝的体积为 (立方米).
例3 先化简,再求值:5a(2a2-5a+3)-2a2(5a+5),
其中a=2.
典例精析
(1)将2x2与5x前面的“-”看成性质符号;
(2)单项式与多项式相乘的结果中,应将同类项合并.
注意
解:5a(2a2-5a+3)-2a2(5a+5)
=10a3-25a2+15a-10a3-10a2
=-35a2+15a,
当a=2时,原式= =-110.
师生互动点评
(1)多项式每一项要包括前面的符号;
(2)单项式须与多项式中每一项相乘,
结果要化到最简;
(3)单项式系数为负时,改变多项式
每项的符号。
我来试一试
1.计算:
(1)(-4x)·(2x2+3x-1)
(2)-2x2·(xy+y2)-5x(x2y-xy2).
2.先化简,再求值:
3a(2a2-4a+3)-2a2(3a+4),其中 a=-2.
我来试一试
(1)(-4x)·(2x2+3x-1)
解:(1)原式
(2)-2x2·(xy+y2)-5x(x2y-xy2).
解:原式=( -2x2) ·xy+(-2x2) ·y2+ (-5x) ·x2y+(-5x) ·(-xy2)
=-2x3y+(-2x2y2)+(-5x3y)+5x2y2
=-7x3y+3x2y2.
2.先化简,再求值3a(2a2-4a+3)-2a2(3a+4),其中
a=-2.
解:3a(2a2-4a+3)-2a2(3a+4)
=6a3-12a2+9a-6a3-8a2
=-20a2+9a.
当a=-2时
原式=-20×(-2)2+9×(-2)
=-98.
知识梳理
通过今天的学习,用你自己的话说说你的收获和体会。
1.单项式乘以多项式的法则
2.在应用单项式乘以多项式的法则进行运算时应注意哪些问题?
3.数形结合、转化、归纳等数
学思想与方法.
再
见
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
