北师大版七年级数学下册 5.3 生活中的轴对称复习课 课件(共16张PPT)
文档属性
| 名称 | 北师大版七年级数学下册 5.3 生活中的轴对称复习课 课件(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 742.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-27 17:05:16 | ||
图片预览

文档简介
(共16张PPT)
第五章 生活中的轴对称
回顾与思考
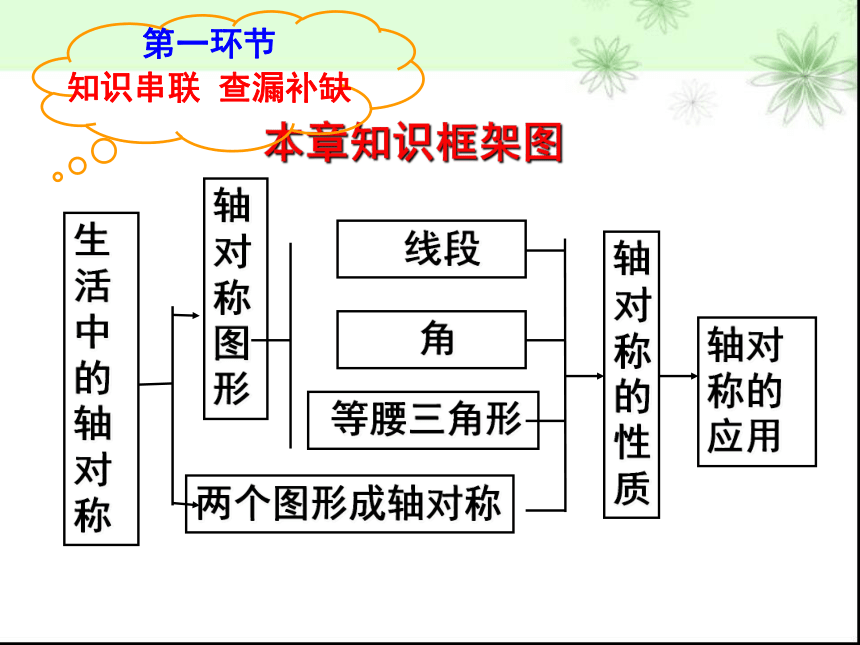
生活中的轴对称
轴对称的性质
轴对称图形
两个图形成轴对称
线段
角
等腰三角形
轴对称的应用
本章知识框架图
第一环节
知识串联 查漏补缺
A
C
B
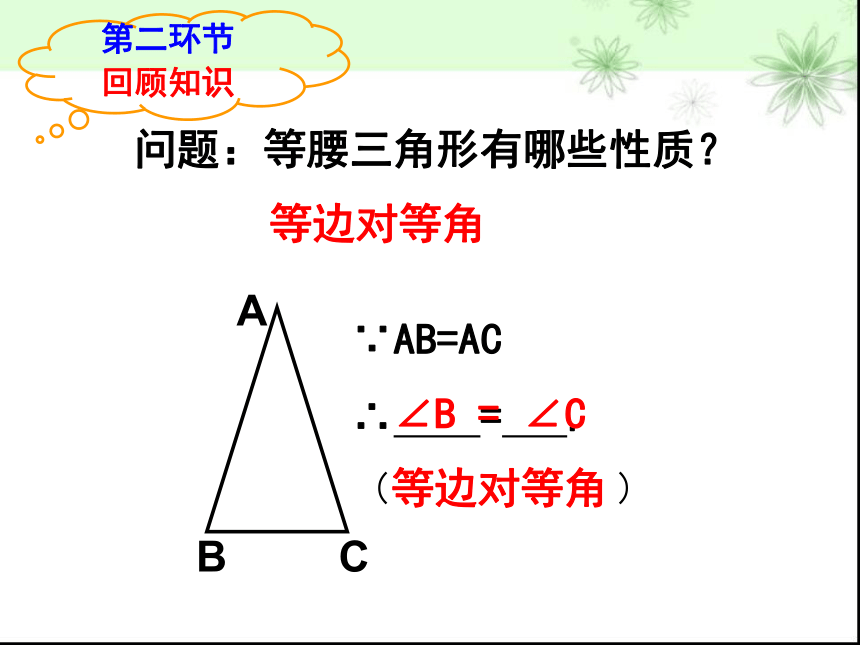
∵AB=AC
∴ = .
( )
∠B = ∠C
等边对等角
第二环节
回顾知识
问题:等腰三角形有哪些性质?
等边对等角
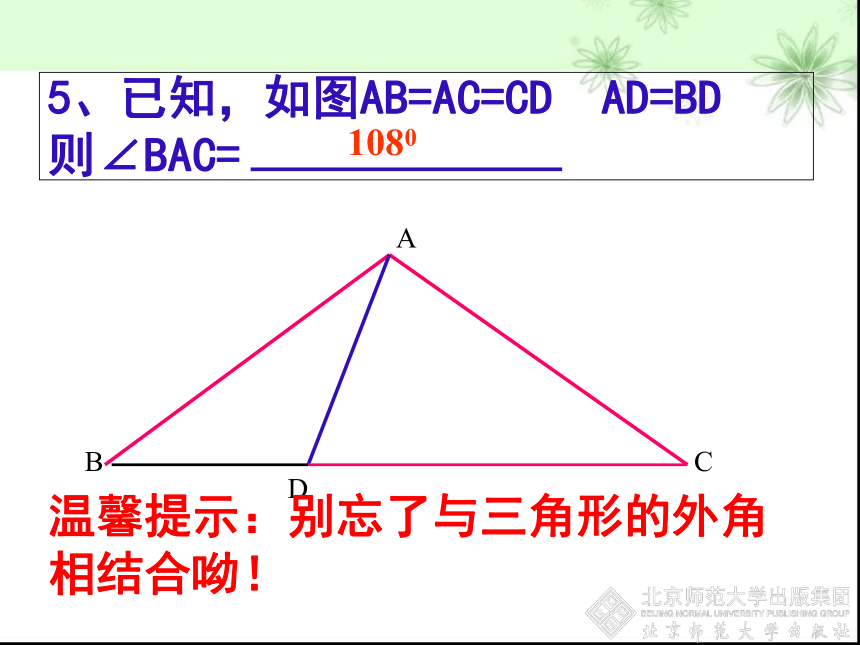
5、已知,如图AB=AC=CD AD=BD
则∠BAC=
A
B
C
D
1080
温馨提示:别忘了与三角形的外角相结合呦!
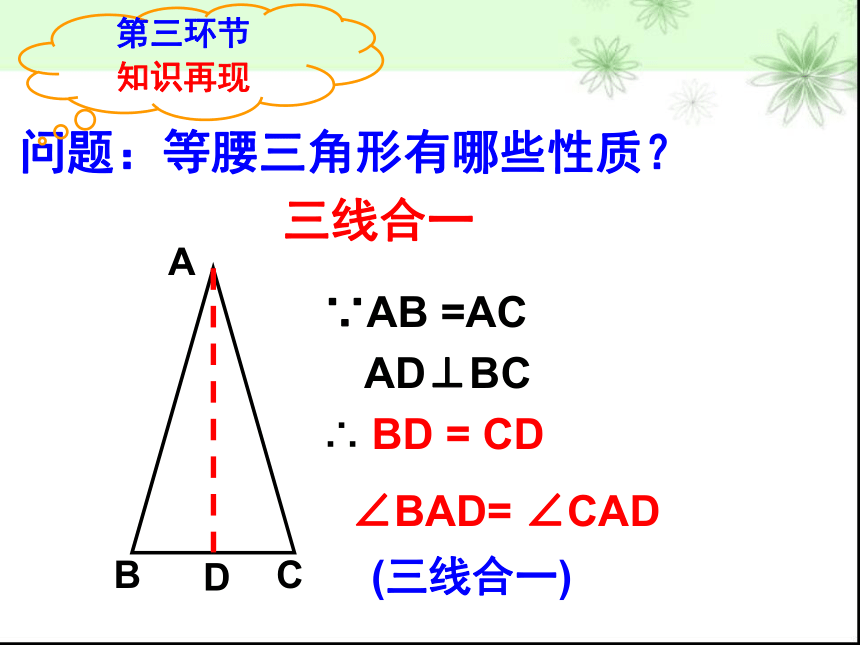
问题:等腰三角形有哪些性质?
A
C
B
D
三线合一
∵AB =AC
(三线合一)
AD⊥BC
∴ BD = CD
∠BAD= ∠CAD
第三环节
知识再现
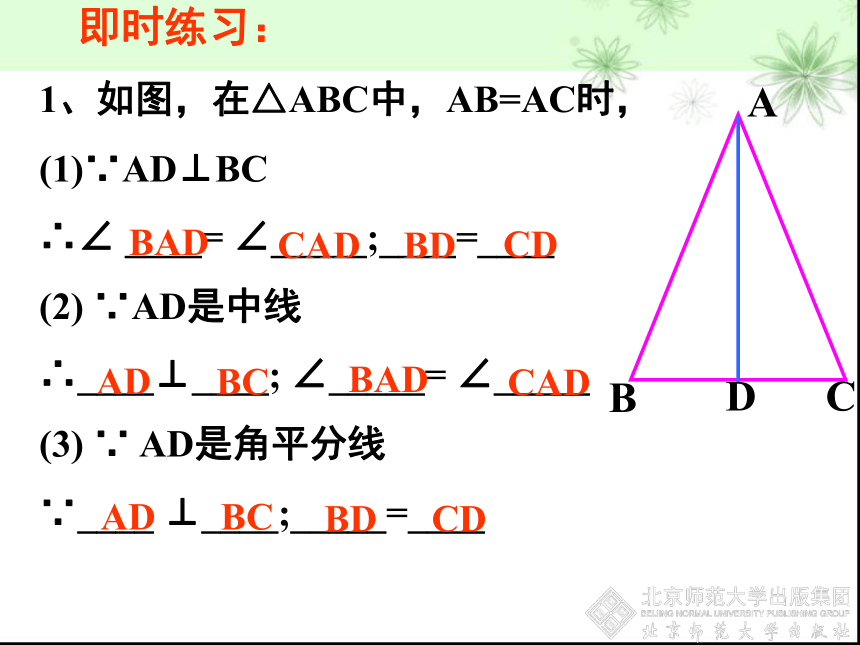
1、如图,在△ABC中,AB=AC时,
(1)∵AD⊥BC
∴∠ ____= ∠_____;____=____
(2) ∵AD是中线
∴____⊥____; ∠_____= ∠_____
(3) ∵ AD是角平分线
∵____ ⊥____;_____=____
B
A
C
D
BAD
CAD
BD
CD
AD
BC
BAD
CAD
AD
BC
BD
CD
即时练习:
本章总结提升
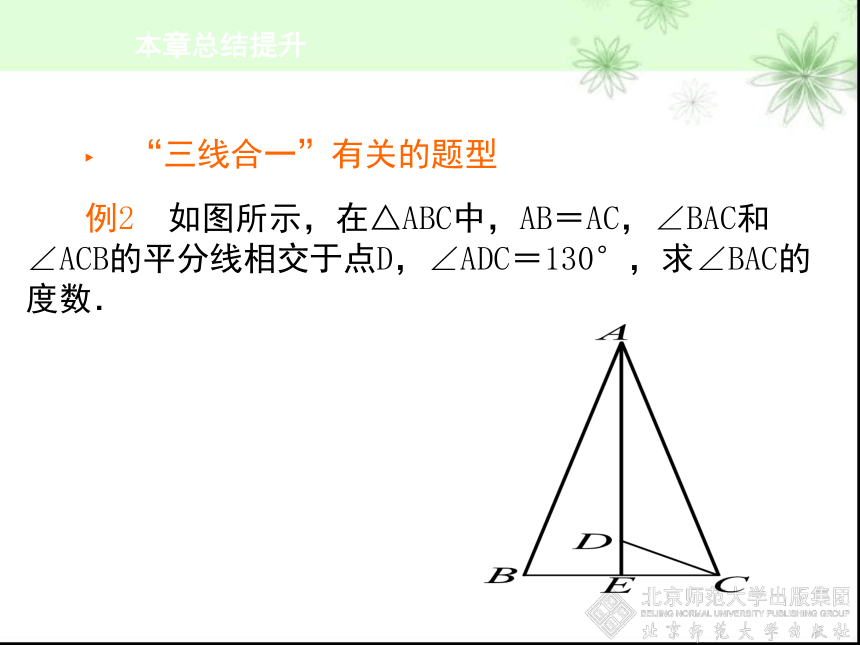
“三线合一”有关的题型
例2 如图所示,在△ABC中,AB=AC,∠BAC和∠ACB的平分线相交于点D,∠ADC=130°,求∠BAC的度数.
课堂精讲
类比精练2.在△ABC中,AB=AC,AD⊥BC,
∠BAD=40°,AD=AE.
求∠CDE的度数.
解:∵AB=AC,AD⊥BC,
∴∠CAD=∠BAD=40°,
∠ADC=90°,
又∵AD=AE,
∴∠ADE= =70°,
∴∠CDE=90°﹣70°=20°.
∵点M在线段AB的垂直平分线上
∴ MA = MB .
第四环节
知识串联
问题:线段的垂直平分线有哪些性质?
线段垂直平分线上的点到这条线段两个端点的距离相等。
本章总结提升
类型三 线段垂直平分线的应用
例3 如图所示,已知AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D.
(1)求∠DBC的度数;
(2)若△DBC的周长为14 cm,BC=5 cm,求AB的长.
第五环节
同场竞技,综合提升
⑤如图5.5—9,△ABC中,AB=AC,BE∥AC,∠BDE=100°,∠BAD=70°,则∠E=_______.
⑥如图5.5—10,在Rt△ABC中,∠B为直角,DE是AC的垂直平分线,E在BC上,∠BAE:∠BAC=1:5,则∠C=_________.
5.5—9
5.5—10
500
400
1.你学到了哪些知识?
2.你学会了哪些方法?
3.你认为应注意哪些问题?
4.你还有哪些困惑?
第六环节
学有所思,布置作业
学有所思
2.如图: 点B、C、D、E、F在∠MAN的边上, ∠A=15o, AB=BC=CD=DE=EF,求∠MEF的度数。
A
B
C
D
E
F
M
N
春天不播种,
夏天就不生长,
秋天不能收获,
冬天就不能品尝。
第五章 生活中的轴对称
回顾与思考
生活中的轴对称
轴对称的性质
轴对称图形
两个图形成轴对称
线段
角
等腰三角形
轴对称的应用
本章知识框架图
第一环节
知识串联 查漏补缺
A
C
B
∵AB=AC
∴ = .
( )
∠B = ∠C
等边对等角
第二环节
回顾知识
问题:等腰三角形有哪些性质?
等边对等角
5、已知,如图AB=AC=CD AD=BD
则∠BAC=
A
B
C
D
1080
温馨提示:别忘了与三角形的外角相结合呦!
问题:等腰三角形有哪些性质?
A
C
B
D
三线合一
∵AB =AC
(三线合一)
AD⊥BC
∴ BD = CD
∠BAD= ∠CAD
第三环节
知识再现
1、如图,在△ABC中,AB=AC时,
(1)∵AD⊥BC
∴∠ ____= ∠_____;____=____
(2) ∵AD是中线
∴____⊥____; ∠_____= ∠_____
(3) ∵ AD是角平分线
∵____ ⊥____;_____=____
B
A
C
D
BAD
CAD
BD
CD
AD
BC
BAD
CAD
AD
BC
BD
CD
即时练习:
本章总结提升
“三线合一”有关的题型
例2 如图所示,在△ABC中,AB=AC,∠BAC和∠ACB的平分线相交于点D,∠ADC=130°,求∠BAC的度数.
课堂精讲
类比精练2.在△ABC中,AB=AC,AD⊥BC,
∠BAD=40°,AD=AE.
求∠CDE的度数.
解:∵AB=AC,AD⊥BC,
∴∠CAD=∠BAD=40°,
∠ADC=90°,
又∵AD=AE,
∴∠ADE= =70°,
∴∠CDE=90°﹣70°=20°.
∵点M在线段AB的垂直平分线上
∴ MA = MB .
第四环节
知识串联
问题:线段的垂直平分线有哪些性质?
线段垂直平分线上的点到这条线段两个端点的距离相等。
本章总结提升
类型三 线段垂直平分线的应用
例3 如图所示,已知AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D.
(1)求∠DBC的度数;
(2)若△DBC的周长为14 cm,BC=5 cm,求AB的长.
第五环节
同场竞技,综合提升
⑤如图5.5—9,△ABC中,AB=AC,BE∥AC,∠BDE=100°,∠BAD=70°,则∠E=_______.
⑥如图5.5—10,在Rt△ABC中,∠B为直角,DE是AC的垂直平分线,E在BC上,∠BAE:∠BAC=1:5,则∠C=_________.
5.5—9
5.5—10
500
400
1.你学到了哪些知识?
2.你学会了哪些方法?
3.你认为应注意哪些问题?
4.你还有哪些困惑?
第六环节
学有所思,布置作业
学有所思
2.如图: 点B、C、D、E、F在∠MAN的边上, ∠A=15o, AB=BC=CD=DE=EF,求∠MEF的度数。
A
B
C
D
E
F
M
N
春天不播种,
夏天就不生长,
秋天不能收获,
冬天就不能品尝。
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
