北师大版七年级数学下册4.3探索三角形全等的条件(第3课时)课件(共19张PPT)
文档属性
| 名称 | 北师大版七年级数学下册4.3探索三角形全等的条件(第3课时)课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 15.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-27 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
探索三角形全等的条件
(第3课时)
三
角
形
快乐课堂我做主
温故知新
壹
壹
贰
壹
叁
壹
边边边(SSS)
角边角(ASA)
角角边(AAS)
到目前为止,你知道哪些判定三角形全等的方法?
(2)两边及其一边的对角
(1)两边及夹角
两边一角相等
想一想
根据探索三角形全等的条件,至少需要三个条件,除了上述三种情况外,还有哪种情况?
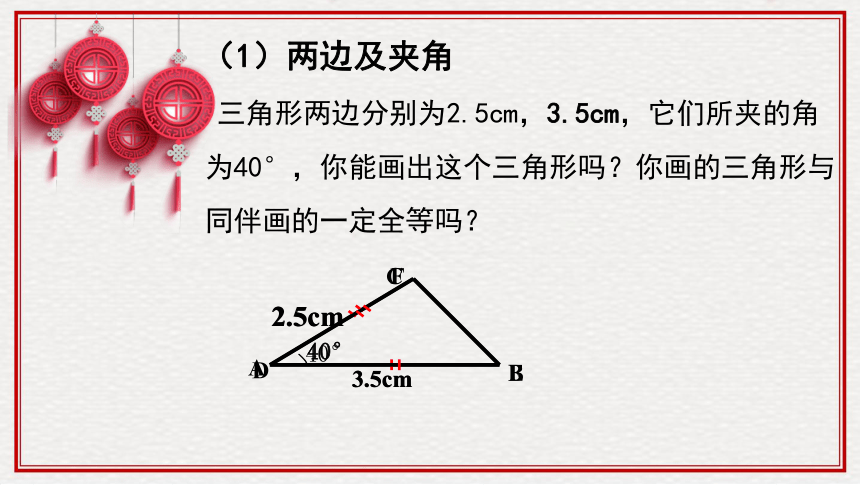
(1)两边及夹角
三角形两边分别为2.5cm,3.5cm,它们所夹的角
为40°,你能画出这个三角形吗?你画的三角形与
同伴画的一定全等吗?
3.5cm
2.5cm
40°
A
B
C
3.5cm
2.5cm
40°
D
E
F
结论:两边和它们的夹角对应相等的两个三角形全等,简写为“边角边”或“SAS”。
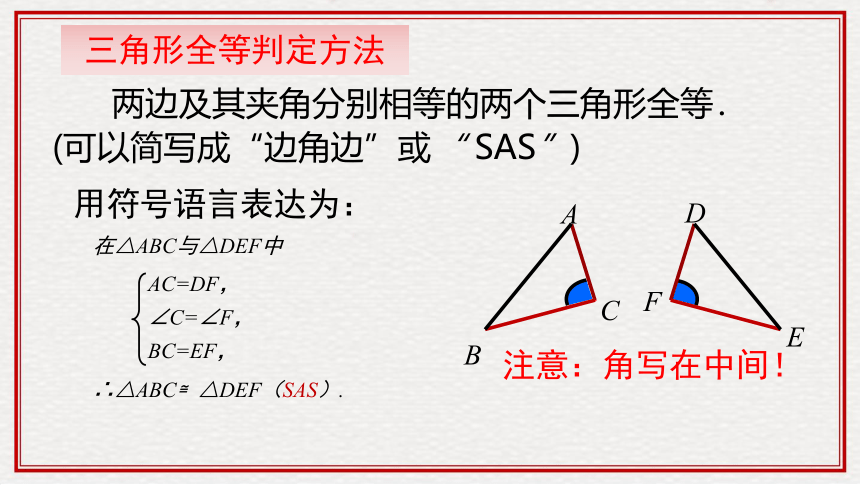
三角形全等判定方法
用符号语言表达为:
在△ABC与△DEF中
∴△ABC≌△DEF(SAS).
两边及其夹角分别相等的两个三角形全等.
(可以简写成“边角边”或“ SAS”)
F
E
D
C
B
A
AC=DF,
∠C=∠F,
BC=EF,
注意:角写在中间!
以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40°,情况又怎样?动手画一画,你发现了什么?
(2)两边及其中一边的对角
B
C
A
2.5cm
3.5cm
40°
结论:两边及其一边所对的角对应相等,两个三角形不一定 全等。
E
D
F
40°
3.5cm
2.5cm
分别找出各题中的全等三角形
A
B
C
40°
40°
D
E
F
(1)
D
C
A
B
(2)
△ABC≌△EFD (SAS)
△ADC≌△CBA (SAS)
练一练
小明做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,小明不用测量就能知道EH=FH吗?
E
F
H
D
在△ABC中,AB=AC,AD是∠BAC的角平分线。那么BD与CD相等吗?为什么?
补充练习
C
D
B
A
解:相等
理由:∵AD是∠BAC的角平分线
∴∠BAD=∠CAD
∵AB=AC
∠BAD=∠CAD
AD=AD
∴△ABD≌△ACD(SAS)
∴BD=CD
由前边题目可以看出:
因为全等三角形的对应角相等,对应边相等,所以,证明分别属于两个三角形的线段相等或角相等的问题,常常通过证明两个三角形全等来解决。
如图,已知AB=AC,AD=AE。那么∠B与∠C相等吗?为什么?
C
D
E
A
B
解:相等
理由:在△ABD和△ACE中
AB=AC
∠A= ∠A
AD=AE
∴△ABD≌△ACE(SAS)
∴∠B=∠C
如图,∠B=∠E,AB=EF,BD=EC,那么△ABC与△FED全等吗?为什么?
AC∥FD吗?为什么?
F
E
D
C
B
A
4
3
1
2
解:全等。
∵BD=EC ∴BD-CD=EC-CD。
即BC=ED
在△ABC与△FED中
AB=FE(已知)
∠B=∠E(已知)
BC=ED(已证)
∴△ABC≌△FED(SAS)
∴∠1=∠2
∴∠3=∠4
∴AC∥FD
小颖作业本上画的三角形被墨迹污染,她想画出一个与原来完全一样的三角形,她该怎么办呢 你能帮帮小颖吗
学以致用
你有哪些收获
1
2
3
今天我们学习哪种方法判定两三角形全等?
通过这节课,判定三角形全等的条件有哪些?
在这四种说明三角形全等的条件中,你发现了什么?
注意:“边边角”不能判定两个三角形全等
SSS,SAS,
ASA,AAS
边角边(SAS)
至少有一个
条件:边相等
习题3.8 1,4
祝
你
成
功
布置作业
不经历风雨,
怎能见彩虹!
结束寄语
再见!
探索三角形全等的条件
(第3课时)
三
角
形
快乐课堂我做主
温故知新
壹
壹
贰
壹
叁
壹
边边边(SSS)
角边角(ASA)
角角边(AAS)
到目前为止,你知道哪些判定三角形全等的方法?
(2)两边及其一边的对角
(1)两边及夹角
两边一角相等
想一想
根据探索三角形全等的条件,至少需要三个条件,除了上述三种情况外,还有哪种情况?
(1)两边及夹角
三角形两边分别为2.5cm,3.5cm,它们所夹的角
为40°,你能画出这个三角形吗?你画的三角形与
同伴画的一定全等吗?
3.5cm
2.5cm
40°
A
B
C
3.5cm
2.5cm
40°
D
E
F
结论:两边和它们的夹角对应相等的两个三角形全等,简写为“边角边”或“SAS”。
三角形全等判定方法
用符号语言表达为:
在△ABC与△DEF中
∴△ABC≌△DEF(SAS).
两边及其夹角分别相等的两个三角形全等.
(可以简写成“边角边”或“ SAS”)
F
E
D
C
B
A
AC=DF,
∠C=∠F,
BC=EF,
注意:角写在中间!
以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40°,情况又怎样?动手画一画,你发现了什么?
(2)两边及其中一边的对角
B
C
A
2.5cm
3.5cm
40°
结论:两边及其一边所对的角对应相等,两个三角形不一定 全等。
E
D
F
40°
3.5cm
2.5cm
分别找出各题中的全等三角形
A
B
C
40°
40°
D
E
F
(1)
D
C
A
B
(2)
△ABC≌△EFD (SAS)
△ADC≌△CBA (SAS)
练一练
小明做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,小明不用测量就能知道EH=FH吗?
E
F
H
D
在△ABC中,AB=AC,AD是∠BAC的角平分线。那么BD与CD相等吗?为什么?
补充练习
C
D
B
A
解:相等
理由:∵AD是∠BAC的角平分线
∴∠BAD=∠CAD
∵AB=AC
∠BAD=∠CAD
AD=AD
∴△ABD≌△ACD(SAS)
∴BD=CD
由前边题目可以看出:
因为全等三角形的对应角相等,对应边相等,所以,证明分别属于两个三角形的线段相等或角相等的问题,常常通过证明两个三角形全等来解决。
如图,已知AB=AC,AD=AE。那么∠B与∠C相等吗?为什么?
C
D
E
A
B
解:相等
理由:在△ABD和△ACE中
AB=AC
∠A= ∠A
AD=AE
∴△ABD≌△ACE(SAS)
∴∠B=∠C
如图,∠B=∠E,AB=EF,BD=EC,那么△ABC与△FED全等吗?为什么?
AC∥FD吗?为什么?
F
E
D
C
B
A
4
3
1
2
解:全等。
∵BD=EC ∴BD-CD=EC-CD。
即BC=ED
在△ABC与△FED中
AB=FE(已知)
∠B=∠E(已知)
BC=ED(已证)
∴△ABC≌△FED(SAS)
∴∠1=∠2
∴∠3=∠4
∴AC∥FD
小颖作业本上画的三角形被墨迹污染,她想画出一个与原来完全一样的三角形,她该怎么办呢 你能帮帮小颖吗
学以致用
你有哪些收获
1
2
3
今天我们学习哪种方法判定两三角形全等?
通过这节课,判定三角形全等的条件有哪些?
在这四种说明三角形全等的条件中,你发现了什么?
注意:“边边角”不能判定两个三角形全等
SSS,SAS,
ASA,AAS
边角边(SAS)
至少有一个
条件:边相等
习题3.8 1,4
祝
你
成
功
布置作业
不经历风雨,
怎能见彩虹!
结束寄语
再见!
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
