北师大版七年级数学下册 4.5 利用全等三角形测距离 课件(共15张PPT)
文档属性
| 名称 | 北师大版七年级数学下册 4.5 利用全等三角形测距离 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-27 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
第三章 三角形
利用三角形全等测距离
1、能利用三角形的全等解决实际问题,体会数学与实际生活的联系
2、能在解决问题的过程中进行有条理的思考和表达
学习目标
在抗日战争期间,为了炸毁与我军阵地隔河相望的日本鬼子的碉堡,需要测出我军阵地到鬼子碉堡的距离。由于没有任何测量工具,我八路军战士为此绞尽脑汁,这时一位聪明的八路军战士想出了一个办法,为成功炸毁碉堡立了一功。
一位经历过战争的老人讲述过这样一个故事:
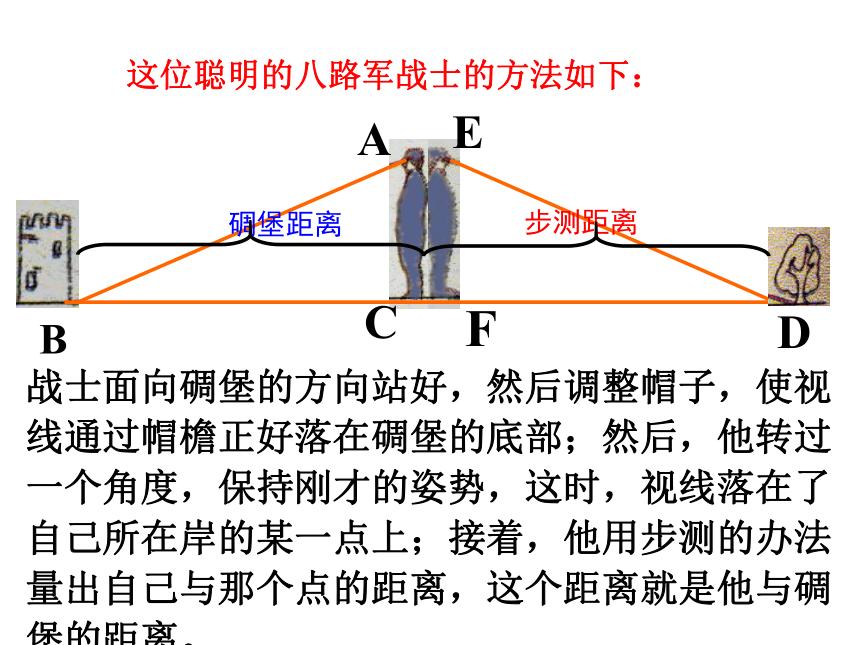
这位聪明的八路军战士的方法如下:
战士面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部;然后,他转过一个角度,保持刚才的姿势,这时,视线落在了自己所在岸的某一点上;接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡的距离。
步测距离
碉堡距离
E
B
F
D
C
A
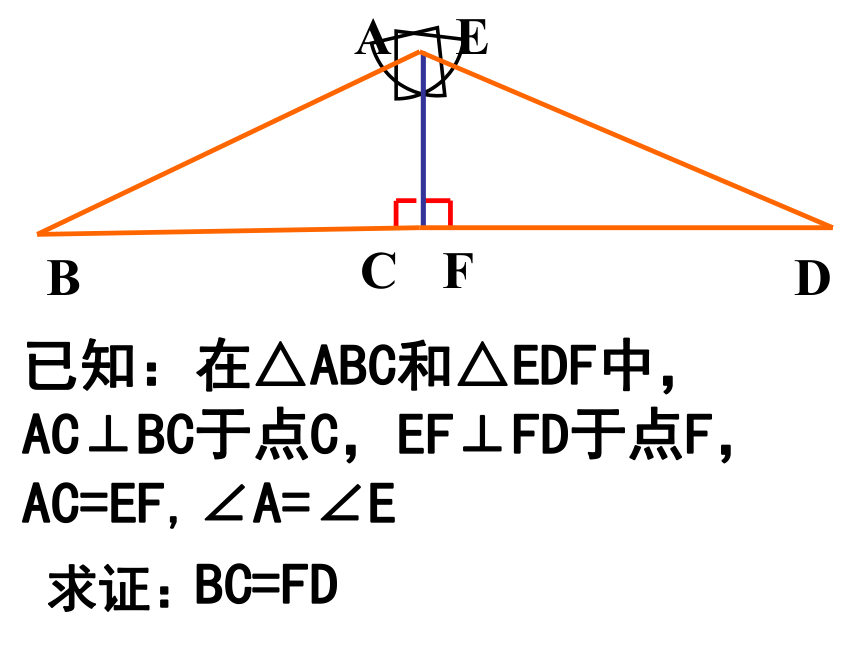
已知:在△ABC和△EDF中,AC⊥BC于点C,EF⊥FD于点F,AC=EF,∠A=∠E
求证:
BC=FD
E
B
F
D
C
A
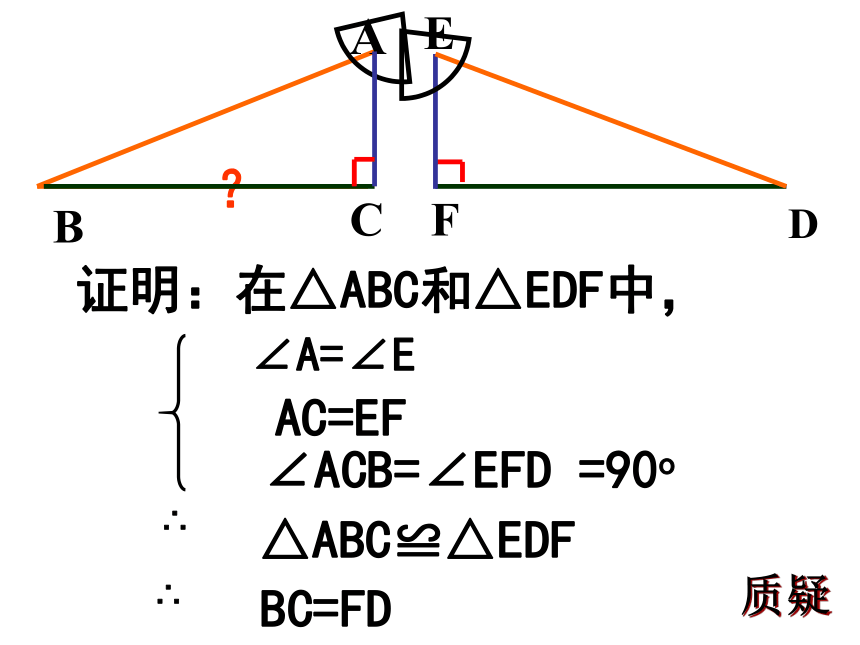
证明:在△ABC和△EDF中,
∠A=∠E
AC=EF
∠ACB=∠EFD =90o
∴
△ABC≌△EDF
∴
BC=FD
E
C
B
D
?
A
F
质疑
1、小明和朋友们在上周末游览风景区时,看到了一个美丽的池塘 ,他们想知道最远两点A、B之间的距离,但是没有船,不能直接去测。手里只有一根绳子和一把尺子,他们怎样才能测出A、B之间的距离呢?
●
B
A
●
A
B
先在地上取一个可以直接到达A和B点的点C,连接AC并延长到D,使CD=AC;连接BC并延长到E,使CE=CB,连接DE并测量出它的长度即为AB的长
返回
已知:如图,△ACB与△DCE,AD、 BE交于点 C,AC=DC, BC=EC
求证:AB=DE
C
E
D
B
A
C
D
1
2
如图,先作三角形ABC,再找一点D,使AD∥BC,并使AD=BC,连结CD,量CD的长即得AB的长
返回
已知:如图,AD∥BC,AD=BC,
求证:AB = CD
B
C
A
D
1
2
已知:如图四边形ABCD中,AD⊥AB于点A,
BC⊥AB于点B,且AD=BC
求证:AB = CD
如图,过点B作BC⊥AB,过点A作
AD ⊥ AB,并使AD=BC,连结CD,量CD的长即得AB的长
如图,找一点D,使AD⊥BD,
B
A
D
C
已知: 如图,在△ABC中, BD ⊥ AC于D,
AD=CD
求证:AB = BC
返回
延长AD至C,使CD=AD,连结BC,量BC的长即得AB的长。
如图,工人师傅要计算一个圆柱形容器的容积,需要测量其内径。现在有两根同样长的木棒、一条橡皮绳和一把带有刻度的直尺,你能想法帮助他完成吗?
·
中点C
A
B
课堂实践(2)
E
F
课堂知识延伸
O
D
C
B
A
课堂小结
1、知识:
利用三角形全等测距离的目的:变不可测距离为可测距离。
依据:全等三角形的性质。
关键:构造全等三角形。
2、方法:(1)延长法构造全等三角形;
(2)垂直法构造全等三角形。
3、数学思想:
树立用三角形全等构建数学模型解决实际问题的思想。
一分耕耘,
一分收获。
回顾与反思
作业:习题3.10
第三章 三角形
利用三角形全等测距离
1、能利用三角形的全等解决实际问题,体会数学与实际生活的联系
2、能在解决问题的过程中进行有条理的思考和表达
学习目标
在抗日战争期间,为了炸毁与我军阵地隔河相望的日本鬼子的碉堡,需要测出我军阵地到鬼子碉堡的距离。由于没有任何测量工具,我八路军战士为此绞尽脑汁,这时一位聪明的八路军战士想出了一个办法,为成功炸毁碉堡立了一功。
一位经历过战争的老人讲述过这样一个故事:
这位聪明的八路军战士的方法如下:
战士面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部;然后,他转过一个角度,保持刚才的姿势,这时,视线落在了自己所在岸的某一点上;接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡的距离。
步测距离
碉堡距离
E
B
F
D
C
A
已知:在△ABC和△EDF中,AC⊥BC于点C,EF⊥FD于点F,AC=EF,∠A=∠E
求证:
BC=FD
E
B
F
D
C
A
证明:在△ABC和△EDF中,
∠A=∠E
AC=EF
∠ACB=∠EFD =90o
∴
△ABC≌△EDF
∴
BC=FD
E
C
B
D
?
A
F
质疑
1、小明和朋友们在上周末游览风景区时,看到了一个美丽的池塘 ,他们想知道最远两点A、B之间的距离,但是没有船,不能直接去测。手里只有一根绳子和一把尺子,他们怎样才能测出A、B之间的距离呢?
●
B
A
●
A
B
先在地上取一个可以直接到达A和B点的点C,连接AC并延长到D,使CD=AC;连接BC并延长到E,使CE=CB,连接DE并测量出它的长度即为AB的长
返回
已知:如图,△ACB与△DCE,AD、 BE交于点 C,AC=DC, BC=EC
求证:AB=DE
C
E
D
B
A
C
D
1
2
如图,先作三角形ABC,再找一点D,使AD∥BC,并使AD=BC,连结CD,量CD的长即得AB的长
返回
已知:如图,AD∥BC,AD=BC,
求证:AB = CD
B
C
A
D
1
2
已知:如图四边形ABCD中,AD⊥AB于点A,
BC⊥AB于点B,且AD=BC
求证:AB = CD
如图,过点B作BC⊥AB,过点A作
AD ⊥ AB,并使AD=BC,连结CD,量CD的长即得AB的长
如图,找一点D,使AD⊥BD,
B
A
D
C
已知: 如图,在△ABC中, BD ⊥ AC于D,
AD=CD
求证:AB = BC
返回
延长AD至C,使CD=AD,连结BC,量BC的长即得AB的长。
如图,工人师傅要计算一个圆柱形容器的容积,需要测量其内径。现在有两根同样长的木棒、一条橡皮绳和一把带有刻度的直尺,你能想法帮助他完成吗?
·
中点C
A
B
课堂实践(2)
E
F
课堂知识延伸
O
D
C
B
A
课堂小结
1、知识:
利用三角形全等测距离的目的:变不可测距离为可测距离。
依据:全等三角形的性质。
关键:构造全等三角形。
2、方法:(1)延长法构造全等三角形;
(2)垂直法构造全等三角形。
3、数学思想:
树立用三角形全等构建数学模型解决实际问题的思想。
一分耕耘,
一分收获。
回顾与反思
作业:习题3.10
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
