苏科版八年级数学下册 11.3 用反比例函数解决问题 课件(共20张PPT)
文档属性
| 名称 | 苏科版八年级数学下册 11.3 用反比例函数解决问题 课件(共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 496.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-27 13:58:14 | ||
图片预览








文档简介
(共20张PPT)
用反比例函数解决问题
什么是反比例函数?
如果两个变量的每一组对应值的乘积是一个不等于0的常数,那么就说这两个变量成反比例。形如 (k为常数,k≠0,x≠0)的函数就叫做反比例函数。
变形公式为
反比例函数的性质是什么?
2. 增减性:当k>0时,在每个象限内y随x增大减小;当k<0时,在每个象限内,y随x增大而增大。
积的不变性:自变量x与其对应的函数y的乘积是定值,等于比例系数k,即
,因此反比例函数图象上任意一点的横坐标与纵坐标的乘积不变,等于比例系数k。
3. 对称性:①轴对称性:反比例函数的图象是轴对称图形,直线 和是它的两条对称轴。 ②中心对称性:反比例函数的图象是中心对称图形,对称中心是坐标原点。
4.面积相等性。
物质的密度ρ是物质的物理属性,它一般不随外界条件的变化而变化。
一定质量的气体,随着体积的变化,它的密度也随之变化。
ρ=
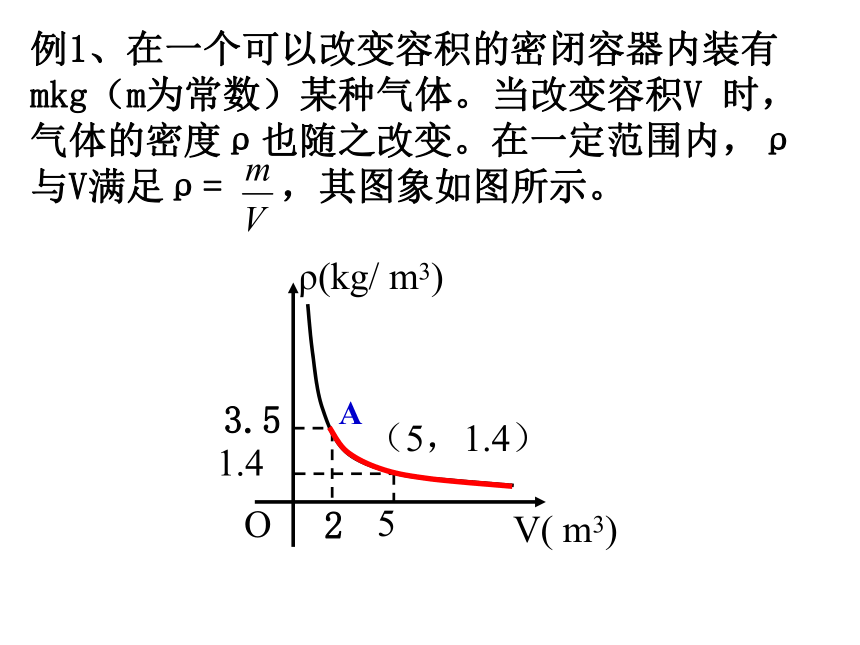
例1、在一个可以改变容积的密闭容器内装有mkg(m为常数)某种气体。当改变容积V 时,气体的密度ρ也随之改变。在一定范围内,ρ与V满足ρ= ,其图象如图所示。
2
1.4
O
ρ(kg/ m3)
(5,1.4)
5
V( m3)
3.5
A
所以蓄水池的底面积S是其深度h的反比例函数
解:(1)由Sh=4×104
变形得S=
例2、某自来水公司计划新建一个容积为4×104m3的长方体蓄水池。
(1)蓄水池的底面积S(m2)与其深度h(m)有怎样的函数关系?
解:把h=5代入S= 得:
所以当蓄水池的深度设计为5m时,蓄水池的底面积应为8000m2
例2、某自来水公司计划新建一个容积为4×104m3的长方体蓄水池。
(2)如果蓄水池的深度设计为5m,那么蓄水池的底面积应为多少平方米?
(3)由于绿化以及辅助用地的需要,经过实地测量,蓄水池的长和宽最多只能分别设计为100m和60m,那么蓄水池的深度至少达到多少才能满足要求?(保留两位小数)
(3)根据题意,得
S=100×60=6000
代入 得:
所以蓄水池的深度至少达到6.67m才能满足要求。
≈6.67
(1) 请你认真分析表格中的数据,确定y是x的什么函数?
例3、某厂从2001年起开始投入技术改进资金,经技术改进后,其产品的生产成本不断降低,具体数据如下表:
年 度 2001 2002 2003 2004
投入技改资金x(万元) 2.5 3 4 4.5
产品成本y(万元/件) 7.2 6 4.5 4
解:(1)因为2.5×7.2=18 3×6=18
4×4.5=18 4.5×4=18
发现 x·y=18 得: y=
所以产品成本y是投入技改资金x的反比例函数
例3、某厂从2001年起开始投入技术改进资金,经技术改进后,其产品的生产成本不断降低,具体数据如下表:
年 度 2001 2002 2003 2004
投入技改资金x(万元) 2.5 3 4 4.5
产品成本y(万元/件) 7.2 6 4.5 4
(2) 按照这种变化规律, 若2005年已投入技改资金5万元,
①预计生产成本每件比2004年降低多少万元?
(2) ①当 x= 5 时,y= =3.6
4-3.6=0.4(万元)
所以,生产成本每件比2004年降低0.4万元。
若2005年已投入技改资金5万元,
②如果打算在2005年把每件产品的成本降低到3.2万元,则还需投入技改资金多少万元?
例3、某厂从2001年起开始投入技术改进资金,经技术改进后,其产品的生产成本不断降低,具体数据如下表:
年 度 2001 2002 2003 2004
投入技改资金x(万元) 2.5 3 4 4.5
产品成本y(万元/件) 7.2 6 4.5 4
4-3.6=0.4(万元)
所以,生产成本每件比2004年降低0.4万元。
②当y=3.2时,3.2=
得x=5.625
5.625-5=0.625(万元)
所以还需投入0.625万元。
(2) ①当 x= 5 时,y= =3.6
为了预防流感,某学校对教室采用药熏消毒法进行消毒, 已知药物燃烧时,室内每立方
6mg,请根据题中所提供的信息,解答下列问题:
米空气中的含药量y(mg)与时间x(min)成正比例。药物燃烧后,y与x成反比例(如图所示),现测得药物8min燃毕,此时室内空气中每立方米的含药量为
6
O
8
x
(
min
)
y
(
mg
)
(1)药物燃烧时,y关于x 的函数关系式为: ______, 自变量x 的取值范围是:_______,药物燃烧后y关于x的函数关系式为______。
6
O
8
x
(
min
)
y
(
mg
)
y= x
0≤x≤8
48
y=
x
(2)研究表明,当空气中每立方米的含药量低于1.6mg时学生方可进教室,那么从消毒开始,至少需要经过______分钟后,学生才能回到教室;
6
O
8
x
(
min
)
y
(
mg
)
30
30
1.6
A
▲如何确定两个变量间是反比例函数关系;
①要注意自变量取值范围符合实际意义;
②确定反比例函数之前一定要考察两个变量与定值之间的关系;
若k未知时应首先由已知条件求出k值。
③求“至少,最多”时可先求关键点,再根据函数性质得到。
▲应用反比例函数解决实际问题时的注意点。
谢谢指导!
用反比例函数解决问题
什么是反比例函数?
如果两个变量的每一组对应值的乘积是一个不等于0的常数,那么就说这两个变量成反比例。形如 (k为常数,k≠0,x≠0)的函数就叫做反比例函数。
变形公式为
反比例函数的性质是什么?
2. 增减性:当k>0时,在每个象限内y随x增大减小;当k<0时,在每个象限内,y随x增大而增大。
积的不变性:自变量x与其对应的函数y的乘积是定值,等于比例系数k,即
,因此反比例函数图象上任意一点的横坐标与纵坐标的乘积不变,等于比例系数k。
3. 对称性:①轴对称性:反比例函数的图象是轴对称图形,直线 和是它的两条对称轴。 ②中心对称性:反比例函数的图象是中心对称图形,对称中心是坐标原点。
4.面积相等性。
物质的密度ρ是物质的物理属性,它一般不随外界条件的变化而变化。
一定质量的气体,随着体积的变化,它的密度也随之变化。
ρ=
例1、在一个可以改变容积的密闭容器内装有mkg(m为常数)某种气体。当改变容积V 时,气体的密度ρ也随之改变。在一定范围内,ρ与V满足ρ= ,其图象如图所示。
2
1.4
O
ρ(kg/ m3)
(5,1.4)
5
V( m3)
3.5
A
所以蓄水池的底面积S是其深度h的反比例函数
解:(1)由Sh=4×104
变形得S=
例2、某自来水公司计划新建一个容积为4×104m3的长方体蓄水池。
(1)蓄水池的底面积S(m2)与其深度h(m)有怎样的函数关系?
解:把h=5代入S= 得:
所以当蓄水池的深度设计为5m时,蓄水池的底面积应为8000m2
例2、某自来水公司计划新建一个容积为4×104m3的长方体蓄水池。
(2)如果蓄水池的深度设计为5m,那么蓄水池的底面积应为多少平方米?
(3)由于绿化以及辅助用地的需要,经过实地测量,蓄水池的长和宽最多只能分别设计为100m和60m,那么蓄水池的深度至少达到多少才能满足要求?(保留两位小数)
(3)根据题意,得
S=100×60=6000
代入 得:
所以蓄水池的深度至少达到6.67m才能满足要求。
≈6.67
(1) 请你认真分析表格中的数据,确定y是x的什么函数?
例3、某厂从2001年起开始投入技术改进资金,经技术改进后,其产品的生产成本不断降低,具体数据如下表:
年 度 2001 2002 2003 2004
投入技改资金x(万元) 2.5 3 4 4.5
产品成本y(万元/件) 7.2 6 4.5 4
解:(1)因为2.5×7.2=18 3×6=18
4×4.5=18 4.5×4=18
发现 x·y=18 得: y=
所以产品成本y是投入技改资金x的反比例函数
例3、某厂从2001年起开始投入技术改进资金,经技术改进后,其产品的生产成本不断降低,具体数据如下表:
年 度 2001 2002 2003 2004
投入技改资金x(万元) 2.5 3 4 4.5
产品成本y(万元/件) 7.2 6 4.5 4
(2) 按照这种变化规律, 若2005年已投入技改资金5万元,
①预计生产成本每件比2004年降低多少万元?
(2) ①当 x= 5 时,y= =3.6
4-3.6=0.4(万元)
所以,生产成本每件比2004年降低0.4万元。
若2005年已投入技改资金5万元,
②如果打算在2005年把每件产品的成本降低到3.2万元,则还需投入技改资金多少万元?
例3、某厂从2001年起开始投入技术改进资金,经技术改进后,其产品的生产成本不断降低,具体数据如下表:
年 度 2001 2002 2003 2004
投入技改资金x(万元) 2.5 3 4 4.5
产品成本y(万元/件) 7.2 6 4.5 4
4-3.6=0.4(万元)
所以,生产成本每件比2004年降低0.4万元。
②当y=3.2时,3.2=
得x=5.625
5.625-5=0.625(万元)
所以还需投入0.625万元。
(2) ①当 x= 5 时,y= =3.6
为了预防流感,某学校对教室采用药熏消毒法进行消毒, 已知药物燃烧时,室内每立方
6mg,请根据题中所提供的信息,解答下列问题:
米空气中的含药量y(mg)与时间x(min)成正比例。药物燃烧后,y与x成反比例(如图所示),现测得药物8min燃毕,此时室内空气中每立方米的含药量为
6
O
8
x
(
min
)
y
(
mg
)
(1)药物燃烧时,y关于x 的函数关系式为: ______, 自变量x 的取值范围是:_______,药物燃烧后y关于x的函数关系式为______。
6
O
8
x
(
min
)
y
(
mg
)
y= x
0≤x≤8
48
y=
x
(2)研究表明,当空气中每立方米的含药量低于1.6mg时学生方可进教室,那么从消毒开始,至少需要经过______分钟后,学生才能回到教室;
6
O
8
x
(
min
)
y
(
mg
)
30
30
1.6
A
▲如何确定两个变量间是反比例函数关系;
①要注意自变量取值范围符合实际意义;
②确定反比例函数之前一定要考察两个变量与定值之间的关系;
若k未知时应首先由已知条件求出k值。
③求“至少,最多”时可先求关键点,再根据函数性质得到。
▲应用反比例函数解决实际问题时的注意点。
谢谢指导!
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
