江苏省苏南四校2012-2013学年高二上学期期中联考数学试卷
文档属性
| 名称 | 江苏省苏南四校2012-2013学年高二上学期期中联考数学试卷 |  | |
| 格式 | zip | ||
| 文件大小 | 188.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-12 22:22:53 | ||
图片预览



文档简介
2012~2013学年第一学期期中考试四校联考
高 二 年级 数学 试卷
命题学校:张家港高级中学 命题:施曙光,审核:章玉龙
【注意】
1.本试卷满分160分,答题时间为120分钟。
2.答案写在答题卷上。
一、填空题:本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上.
1.两个平面最多可以将空间分成 部分.
2.直线的倾斜角是 .
3.已知 .
4.两平行直线的距离是 .
5.已/知圆关于直线成轴对称,则= ..
6.关于直线与平面,有以下四个命题:
①若且,则;②若且,则;
③若且,则;④若且,则;
其中正确命题的序号是 .
7.正三棱锥的底面边长为3,侧棱长为,则其体积为 .
8.过点P(2,3)且在两轴上的截距相等的直线方程是_________________.
9.圆柱形容器的内壁底半径是cm,有一个实心铁球浸没于容器的水中,若取出这个铁球,测得容器的水面下降了cm,则这个铁球的表面积为 .
10.圆心在轴上,且与直线相切于点的圆的方程为________ ___________.
11.点P在平面ABC上的射影为O,且PA、PB、PC两两垂直,那么O是△ABC的 .(填:外心,内心,重心,垂心)
12.若直线与曲线恰有一个公共点,则的取值范围是 .
13.已知直线和直线与两坐标轴围成一个四边形,则使得这个四边形面积最小的值为 .
14.若圆上至少有三个不同的点到直线的距离为,则该直线的斜率的范围是_______________________.
二、解答题:本大题共6小题,共计14+14+15+15+16+16=90分.解答应写出文字说明、证明过程或演算步骤.请把答案写在答卷纸相应位置上.
15(本小题满分14分)
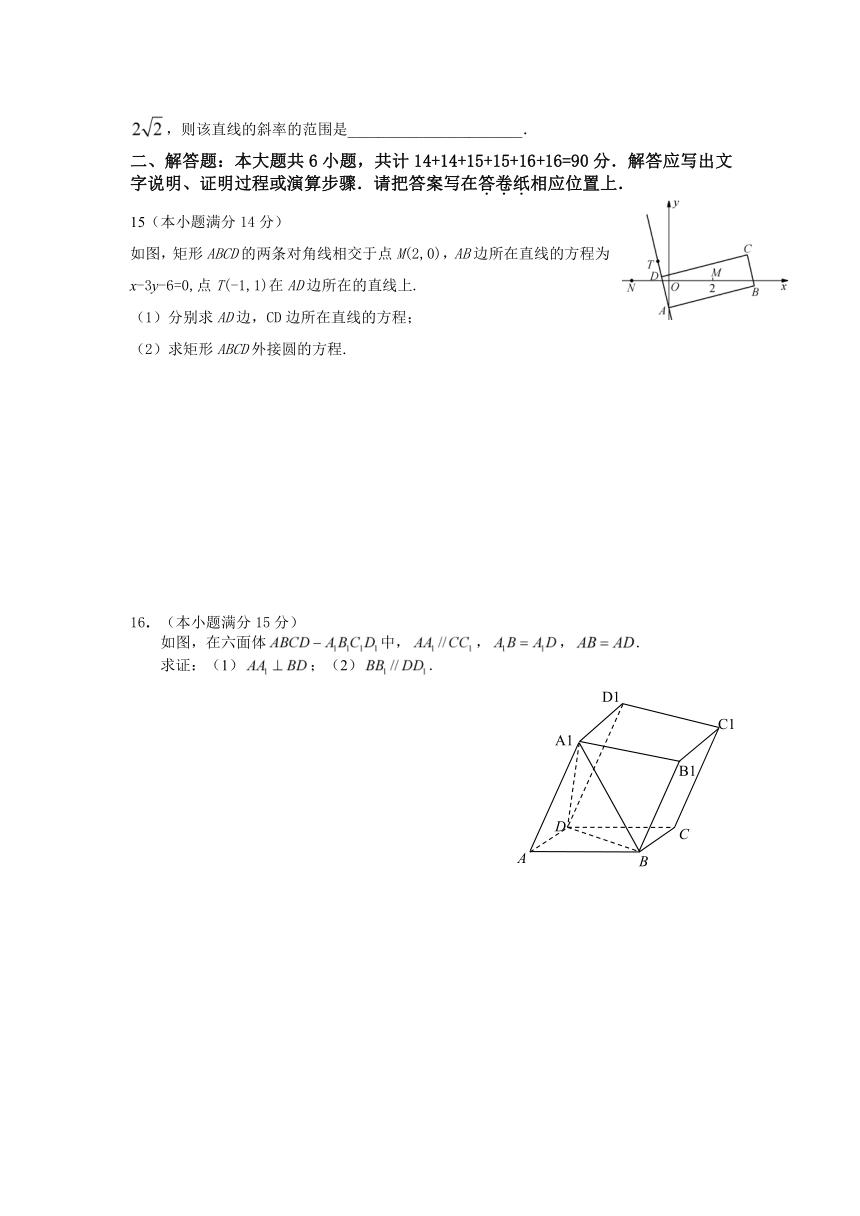
如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点T(-1,1)在AD边所在的直线上.
(1)分别求AD边,CD边所在直线的方程;
(2)求矩形ABCD外接圆的方程.
16.(本小题满分15分)
如图,在六面体中,,,.
求证:(1);(2).
17.(本小题满分15分)
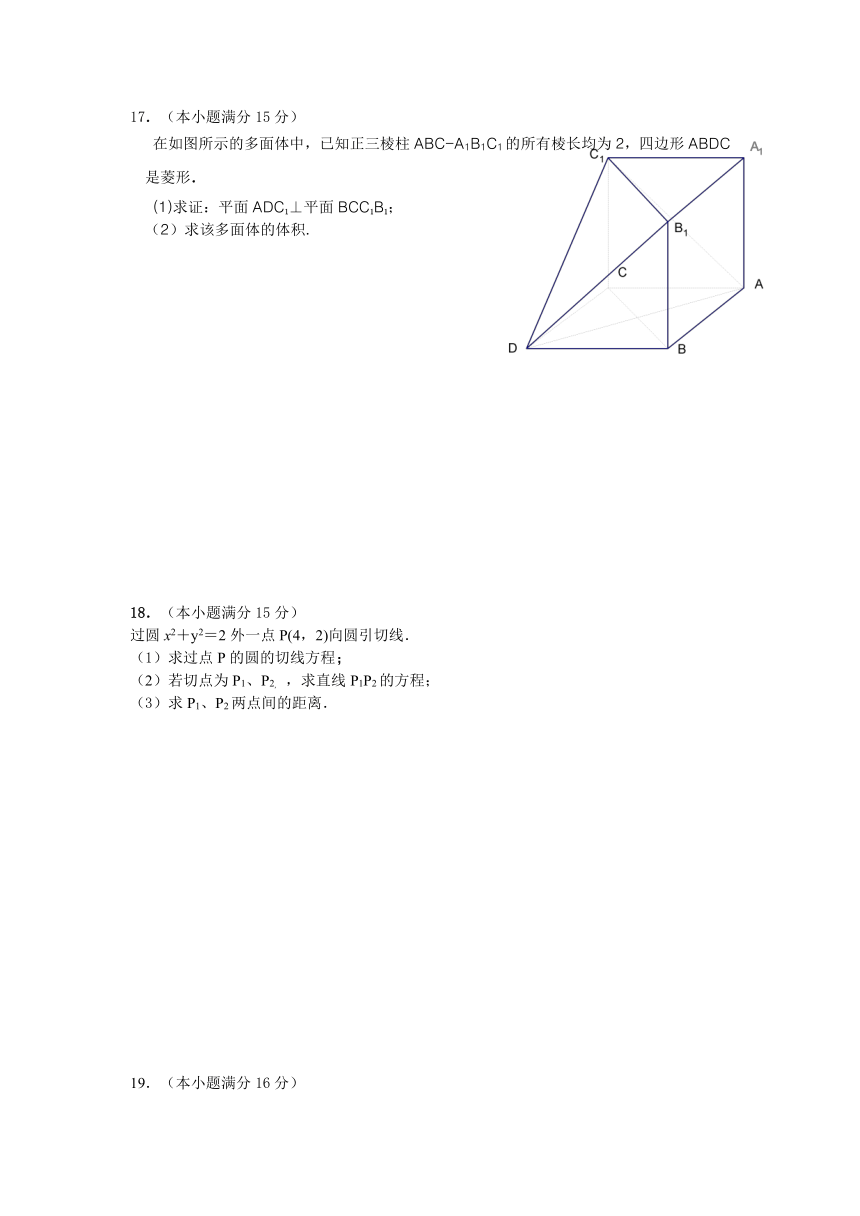
在如图所示的多面体中,已知正三棱柱ABC-A1B1C1的所有棱长均为2,四边形ABDC是菱形.
(1)求证:平面ADC1⊥平面BCC1B1;
(2)求该多面体的体积.
18.(本小题满分15分)
过圆x2+y2=2外一点P(4,2)向圆引切线.
(1)求过点P的圆的切线方程;
(2)若切点为P1、P2, ,求直线P1P2的方程;
(3)求P1、P2两点间的距离.
19.(本小题满分16分)
设圆,动圆.
(1)求证:圆、圆相交于两个定点;
(2)设点P是圆上的点,过点P作圆的一条切线,切点为,过点P作圆的一条切线,切点为,问:是否存在点P,使无穷多个圆,满足?如果存在,求出所有这样的点P;如果不存在,说明理由.
20.(本小题满分16分)
如图,在平面直角坐标系中,已知圆:,圆:.
(1)若过点的直线被圆截得的弦长为,求直线的方程;
(2)设动圆同时平分圆的周长、圆的周长.
①证明:动圆圆心C在一条定直线上运动;
②动圆是否经过定点?若经过,求出定点的
坐标;若不经过,请说明理由.
2012~2013学年第一学期期中考试四校联考
高 二 年级 数学 答题卷
注意事项
答题前请您务必将自己的姓名、考号填在指定位置.答题时请用黑色0.5毫米签字笔写在答题卷的指定位置.在其它位置作答一律无效.如要作图,须用2B铅笔,并加黑加粗.
一、填空题:本大题共14小题,每小题5分,共70分.请将正确答案填写在相应位置。
1. 2. 3.
4. 5. 6.
7. 8. 9.
10. 11. 12.
13. 14.
二、解答题:本大题共6小题,共90分.请在答卷纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.(本小题满分14)
解:
16.(本小题满分14)
解:
17.(本小题满分15分)
解:
18.(本小题满分15分)
解:
19.(本小题满分16分)
解:
20.(本小题满分16分)
解:
2012~2013学年第一学期高二年级期中考试四校联考
数学试卷I
(满分160分,考试时间120分钟)命题:施曙光,审核:章玉龙
一、填空题:本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上.
1.两个平面最多可以将空间分成 部分. 4
2.直线的倾斜角是 .600
3.已知 9或1
4.两平行直线的距离是 。
5.已/知圆关于直线成轴对称,则= . 4
6.关于直线与平面,有以下四个命题:
①若且,则;②若且,则;
③若且,则;④若且,则;
其中正确命题的序号是 ②③
7.正三棱锥的底面边长为3,侧棱长为,则其体积为 .
答案: 9/4
8.过点P(2,3)且在两轴上的截距相等的直线方程是__________________.
9.圆柱形容器的内壁底半径是cm,有一个实心铁球浸没于容器的水中,若取出这个铁球,测得容器的水面下降了cm,则这个铁球的表面积为 ..
10.圆心在轴上,且与直线相切于点的圆的方程为________ ___________.
11.点P在平面ABC上的射影为O,且PA、PB、PC两两垂直,那么O是△ABC的 心垂心;
12.若直线与曲线恰有一个公共点,则的取值范围是 .
(-2,2]{-}
13.已知直线和直线与两坐标轴围成一个四边形,则使得这个四边形面积最小的值为 .1/8
14.若圆上至少有三个不同的点到直线的距离为,则该直线的斜率的范围是_______________________.
答案:
二、解答题:(本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内.)
15(本小题满分14分)
如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点T(-1,1)在AD边所在的直线上.
(1)求AD边,CD边所在直线的方程;
(2)求矩形ABCD外接圆的方程.
解:(1) 因为AB边所在直线的方程为x-3y-6=0,且AD与AB垂直,
所以直线AD的斜率为-3.……………………………………2分
又因为点T(-1,1)在直线AD上,所以AD边所在直线的方程为y-1=-3(x+1),
即3x+y+2=0.…………………………………………………………4分
由解得点A的坐标为(0,-2). …………6分
因为矩形ABCD的两条对角线的交点为M(2,0),所以C(4,2) …………8分
所以CD边所在直线的方程为x-3y+2=0, …………10分
(2) M为矩形ABCD外接圆的圆心.
又|AM|=,………………………………12分
从而矩形ABCD外接圆的方程为(x-2)2+y2=8.…………………… 14分
16.(本小题满分14分)
如图,在六面体中,,,
.求证:(1);(2).
证明:(1)取线段的中点,连结、,
因为,,
所以,.…………3分
又,平面,
所以平面.
而平面,
所以.……………………………7分
(2)因为,
平面,平面,
所以平面.…………………………………………………10分
又平面,平面平面,……11分
所以.同理得,
所以.…………………………………………………14分
17.(本小题满分15分)
在如图所示的多面体中,已知正三棱柱ABC-A1B1C1的所有棱长均为2,四边形ABDC是菱形.
(1)求证:平面ADC1⊥平面BCC1B1
(2)求该多面体的体积.
(1)证:由正三棱柱,得,而四边形是菱形,所以,
又平面且,所以平面…5分
则由平面,得平面平面…………………… 7分
(2)因为正三棱柱的体积为………10分
四棱锥的体积为……………13分
所以该多面体的体积为……………………………………………15分
18.(本小题满分15分)
过⊙:x2+y2=2外一点P(4,2)向圆引切线.
(1)求过点P的圆的切线方程.
(2)若切点为P1、P2求过切点P1、P2的直线方程.
(3)求P1、P2两点间的距离.
解:(1)设过点P(4,2)的切线方程为y-2=k(x-4)
即kx-y+2-4k=0 ①
则d=
∴= 解得k=1或k=…………3分
∴切线方程为:x-y-2=0或x-7y+10=0………………………………………5分
(2) 设切点P1(x1,y1)、P2(x2,y2),则两切线的方程可写成l1: x1x+y1y=2,l2:x2x+y2y=2
因为点(4,2)在l1和l2上.则有4 x1+2y1=2 4x2+2y2=2
这表明两点都在直线4x+2y=2上,由于两点只能确定一条直线,故直线2 x+y-1=0即为所求……………………………………10分
(3)……………………15分
19.(本小题满分16分)
设圆,动圆,
(1)求证:圆、圆相交于两个定点;
(2)设点P是圆上的点,过点P作圆的一条切线,切点为,过点P作圆的一条切线,切点为,问:是否存在点P,使无穷多个圆,满足?如果存在,求出所有这样的点P;如果不存在,说明理由.
19.解(1)将方程化为,
令得或,所以圆过定点和,……………4分
将代入,左边=右边,故点在圆上,同理可得点也在圆上,所以圆、圆相交于两个定点和;……………6分
(2)设,则,…………………………8分, …………………………………10分
即,整理得(*)………………………………………………12分
存在无穷多个圆,满足的条件为(1)有解,
…………………14分
而(1)无解,故不存在点P,使无穷多个圆,满足.………………16分
20(本小题满分16分)
如图,在平面直角坐标系中,已知圆:,圆: .
(1)若过点的直线被圆截得的弦长为,求直线的方程;
(2)设动圆同时平分圆的周长、圆的周长.
①证明:动圆圆心C在一条定直线上运动;
②动圆是否经过定点?若经过,求出定点的
坐标;若不经过,请说明理由.
解:(1)设直线的方程为,即.
因为直线被圆截得的弦长为,而圆的半径为1,
所以圆心到:的距离为.…………………………3分
化简,得,解得或.
所以直线的方程为或.…………………6分
(2)①证明:设圆心,由题意,得,
即.
化简得,
即动圆圆心C在定直线上运动.…………………………10分
②圆过定点,设,
则动圆C的半径为.
于是动圆C的方程为.
整理,得.…………………………14分
由得或
所以定点的坐标为,.………16分
高 二 年级 数学 试卷
命题学校:张家港高级中学 命题:施曙光,审核:章玉龙
【注意】
1.本试卷满分160分,答题时间为120分钟。
2.答案写在答题卷上。
一、填空题:本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上.
1.两个平面最多可以将空间分成 部分.
2.直线的倾斜角是 .
3.已知 .
4.两平行直线的距离是 .
5.已/知圆关于直线成轴对称,则= ..
6.关于直线与平面,有以下四个命题:
①若且,则;②若且,则;
③若且,则;④若且,则;
其中正确命题的序号是 .
7.正三棱锥的底面边长为3,侧棱长为,则其体积为 .
8.过点P(2,3)且在两轴上的截距相等的直线方程是_________________.
9.圆柱形容器的内壁底半径是cm,有一个实心铁球浸没于容器的水中,若取出这个铁球,测得容器的水面下降了cm,则这个铁球的表面积为 .
10.圆心在轴上,且与直线相切于点的圆的方程为________ ___________.
11.点P在平面ABC上的射影为O,且PA、PB、PC两两垂直,那么O是△ABC的 .(填:外心,内心,重心,垂心)
12.若直线与曲线恰有一个公共点,则的取值范围是 .
13.已知直线和直线与两坐标轴围成一个四边形,则使得这个四边形面积最小的值为 .
14.若圆上至少有三个不同的点到直线的距离为,则该直线的斜率的范围是_______________________.
二、解答题:本大题共6小题,共计14+14+15+15+16+16=90分.解答应写出文字说明、证明过程或演算步骤.请把答案写在答卷纸相应位置上.
15(本小题满分14分)
如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点T(-1,1)在AD边所在的直线上.
(1)分别求AD边,CD边所在直线的方程;
(2)求矩形ABCD外接圆的方程.
16.(本小题满分15分)
如图,在六面体中,,,.
求证:(1);(2).
17.(本小题满分15分)
在如图所示的多面体中,已知正三棱柱ABC-A1B1C1的所有棱长均为2,四边形ABDC是菱形.
(1)求证:平面ADC1⊥平面BCC1B1;
(2)求该多面体的体积.
18.(本小题满分15分)
过圆x2+y2=2外一点P(4,2)向圆引切线.
(1)求过点P的圆的切线方程;
(2)若切点为P1、P2, ,求直线P1P2的方程;
(3)求P1、P2两点间的距离.
19.(本小题满分16分)
设圆,动圆.
(1)求证:圆、圆相交于两个定点;
(2)设点P是圆上的点,过点P作圆的一条切线,切点为,过点P作圆的一条切线,切点为,问:是否存在点P,使无穷多个圆,满足?如果存在,求出所有这样的点P;如果不存在,说明理由.
20.(本小题满分16分)
如图,在平面直角坐标系中,已知圆:,圆:.
(1)若过点的直线被圆截得的弦长为,求直线的方程;
(2)设动圆同时平分圆的周长、圆的周长.
①证明:动圆圆心C在一条定直线上运动;
②动圆是否经过定点?若经过,求出定点的
坐标;若不经过,请说明理由.
2012~2013学年第一学期期中考试四校联考
高 二 年级 数学 答题卷
注意事项
答题前请您务必将自己的姓名、考号填在指定位置.答题时请用黑色0.5毫米签字笔写在答题卷的指定位置.在其它位置作答一律无效.如要作图,须用2B铅笔,并加黑加粗.
一、填空题:本大题共14小题,每小题5分,共70分.请将正确答案填写在相应位置。
1. 2. 3.
4. 5. 6.
7. 8. 9.
10. 11. 12.
13. 14.
二、解答题:本大题共6小题,共90分.请在答卷纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.(本小题满分14)
解:
16.(本小题满分14)
解:
17.(本小题满分15分)
解:
18.(本小题满分15分)
解:
19.(本小题满分16分)
解:
20.(本小题满分16分)
解:
2012~2013学年第一学期高二年级期中考试四校联考
数学试卷I
(满分160分,考试时间120分钟)命题:施曙光,审核:章玉龙
一、填空题:本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上.
1.两个平面最多可以将空间分成 部分. 4
2.直线的倾斜角是 .600
3.已知 9或1
4.两平行直线的距离是 。
5.已/知圆关于直线成轴对称,则= . 4
6.关于直线与平面,有以下四个命题:
①若且,则;②若且,则;
③若且,则;④若且,则;
其中正确命题的序号是 ②③
7.正三棱锥的底面边长为3,侧棱长为,则其体积为 .
答案: 9/4
8.过点P(2,3)且在两轴上的截距相等的直线方程是__________________.
9.圆柱形容器的内壁底半径是cm,有一个实心铁球浸没于容器的水中,若取出这个铁球,测得容器的水面下降了cm,则这个铁球的表面积为 ..
10.圆心在轴上,且与直线相切于点的圆的方程为________ ___________.
11.点P在平面ABC上的射影为O,且PA、PB、PC两两垂直,那么O是△ABC的 心垂心;
12.若直线与曲线恰有一个公共点,则的取值范围是 .
(-2,2]{-}
13.已知直线和直线与两坐标轴围成一个四边形,则使得这个四边形面积最小的值为 .1/8
14.若圆上至少有三个不同的点到直线的距离为,则该直线的斜率的范围是_______________________.
答案:
二、解答题:(本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内.)
15(本小题满分14分)
如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点T(-1,1)在AD边所在的直线上.
(1)求AD边,CD边所在直线的方程;
(2)求矩形ABCD外接圆的方程.
解:(1) 因为AB边所在直线的方程为x-3y-6=0,且AD与AB垂直,
所以直线AD的斜率为-3.……………………………………2分
又因为点T(-1,1)在直线AD上,所以AD边所在直线的方程为y-1=-3(x+1),
即3x+y+2=0.…………………………………………………………4分
由解得点A的坐标为(0,-2). …………6分
因为矩形ABCD的两条对角线的交点为M(2,0),所以C(4,2) …………8分
所以CD边所在直线的方程为x-3y+2=0, …………10分
(2) M为矩形ABCD外接圆的圆心.
又|AM|=,………………………………12分
从而矩形ABCD外接圆的方程为(x-2)2+y2=8.…………………… 14分
16.(本小题满分14分)
如图,在六面体中,,,
.求证:(1);(2).
证明:(1)取线段的中点,连结、,
因为,,
所以,.…………3分
又,平面,
所以平面.
而平面,
所以.……………………………7分
(2)因为,
平面,平面,
所以平面.…………………………………………………10分
又平面,平面平面,……11分
所以.同理得,
所以.…………………………………………………14分
17.(本小题满分15分)
在如图所示的多面体中,已知正三棱柱ABC-A1B1C1的所有棱长均为2,四边形ABDC是菱形.
(1)求证:平面ADC1⊥平面BCC1B1
(2)求该多面体的体积.
(1)证:由正三棱柱,得,而四边形是菱形,所以,
又平面且,所以平面…5分
则由平面,得平面平面…………………… 7分
(2)因为正三棱柱的体积为………10分
四棱锥的体积为……………13分
所以该多面体的体积为……………………………………………15分
18.(本小题满分15分)
过⊙:x2+y2=2外一点P(4,2)向圆引切线.
(1)求过点P的圆的切线方程.
(2)若切点为P1、P2求过切点P1、P2的直线方程.
(3)求P1、P2两点间的距离.
解:(1)设过点P(4,2)的切线方程为y-2=k(x-4)
即kx-y+2-4k=0 ①
则d=
∴= 解得k=1或k=…………3分
∴切线方程为:x-y-2=0或x-7y+10=0………………………………………5分
(2) 设切点P1(x1,y1)、P2(x2,y2),则两切线的方程可写成l1: x1x+y1y=2,l2:x2x+y2y=2
因为点(4,2)在l1和l2上.则有4 x1+2y1=2 4x2+2y2=2
这表明两点都在直线4x+2y=2上,由于两点只能确定一条直线,故直线2 x+y-1=0即为所求……………………………………10分
(3)……………………15分
19.(本小题满分16分)
设圆,动圆,
(1)求证:圆、圆相交于两个定点;
(2)设点P是圆上的点,过点P作圆的一条切线,切点为,过点P作圆的一条切线,切点为,问:是否存在点P,使无穷多个圆,满足?如果存在,求出所有这样的点P;如果不存在,说明理由.
19.解(1)将方程化为,
令得或,所以圆过定点和,……………4分
将代入,左边=右边,故点在圆上,同理可得点也在圆上,所以圆、圆相交于两个定点和;……………6分
(2)设,则,…………………………8分, …………………………………10分
即,整理得(*)………………………………………………12分
存在无穷多个圆,满足的条件为(1)有解,
…………………14分
而(1)无解,故不存在点P,使无穷多个圆,满足.………………16分
20(本小题满分16分)
如图,在平面直角坐标系中,已知圆:,圆: .
(1)若过点的直线被圆截得的弦长为,求直线的方程;
(2)设动圆同时平分圆的周长、圆的周长.
①证明:动圆圆心C在一条定直线上运动;
②动圆是否经过定点?若经过,求出定点的
坐标;若不经过,请说明理由.
解:(1)设直线的方程为,即.
因为直线被圆截得的弦长为,而圆的半径为1,
所以圆心到:的距离为.…………………………3分
化简,得,解得或.
所以直线的方程为或.…………………6分
(2)①证明:设圆心,由题意,得,
即.
化简得,
即动圆圆心C在定直线上运动.…………………………10分
②圆过定点,设,
则动圆C的半径为.
于是动圆C的方程为.
整理,得.…………………………14分
由得或
所以定点的坐标为,.………16分
同课章节目录
