第十章 三角形的有关证明专题训练 等腰三角形的性质与判定的综合应用(含答案)
文档属性
| 名称 | 第十章 三角形的有关证明专题训练 等腰三角形的性质与判定的综合应用(含答案) | 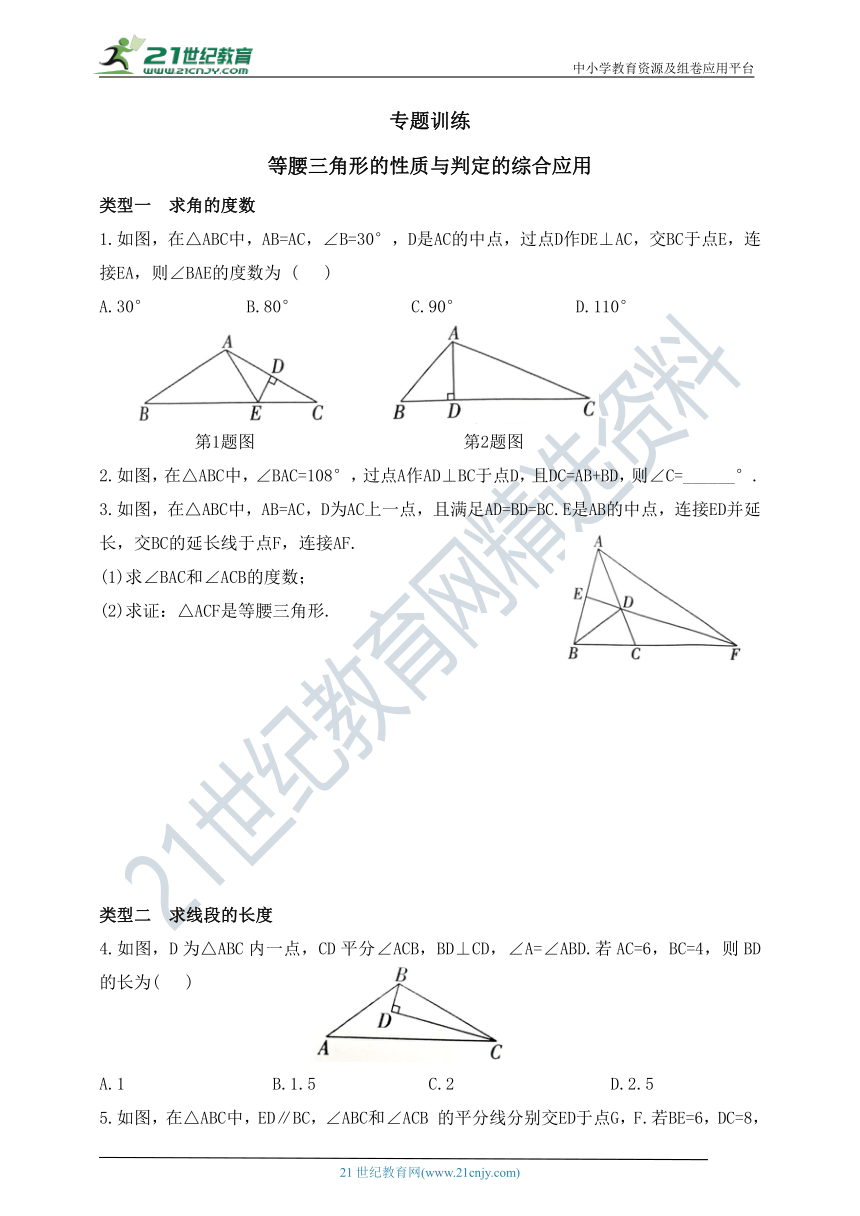 | |
| 格式 | docx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-27 17:33:25 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
专题训练
等腰三角形的性质与判定的综合应用
类型一 求角的度数
1.如图,在△ABC中,AB=AC,∠B=30°,D是AC的中点,过点D作DE⊥AC,交BC于点E,连接EA,则∠BAE的度数为 ( )
A.30° B.80° C.90° D.110°
第1题图 第2题图
2.如图,在△ABC中,∠BAC=108°,过点A作AD⊥BC于点D,且DC=AB+BD,则∠C=______°.
3.如图,在△ABC中,AB=AC,D为AC上一点,且满足AD=BD=BC.E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF.
(1)求∠BAC和∠ACB的度数;
(2)求证:△ACF是等腰三角形.
类型二 求线段的长度
4.如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD.若AC=6,BC=4,则BD的长为( )
A.1 B.1.5 C.2 D.2.5
5.如图,在△ABC中,ED∥BC,∠ABC和∠ACB 的平分线分别交ED于点G,F.若BE=6,DC=8,DE=20,则FG=_________.
6.已知在△ABC中,∠ACB的平分线CD交AB 于点D,DE∥BC.
(1)如图①,如果E是边AC的中点,AC=8,求:DE的长;
(2)如图②,DE平分∠ADC,∠B=30°,在边BC上取点F使BF=DF,若BC=9,求DF 的长.
类型三 判断三角形的形状
7.如图,在△ABC中,∠ABC=90°,∠C=30°,AD是∠BAC 的平分线,DE⊥AC于点E,AD,BE相交于点F,则图中的等腰三角形有( )
A.2个 B.3个 C.4个 D.5个
8.已知D为△ABC所在平面内一点,且DB=DC,DE⊥AB,DF⊥AC,垂足分别为E,F,DE=DF.
(1)如图,当点D在边BC上时,判断△ABC的形状(直接写出答案).
(2)当点D在△ABC内部时,(1)中的结论仍成立吗?若成立,请说明理由;若不成立,请举出反例(画图说明).
(3)当点D在△ABC外部时,(1)中的结论仍成立吗?若成立,请说明理由;若不成立,请举出反例(画图说明).
类型四 分类讨论思想的应用
9.已知一个等腰三角形一腰上的高与另一腰的夹角是50°,则这个等腰三角形的底角为( )
A.70° B.20° C.70°或20° D.40°或140°
10.如图,∠AOB=60°,C是BO延长线上的一点,OC=12cm,动点P从点C出发沿CB以3 cm/s的速度移动,动点Q从点O出发沿OA以2 cm/s的速度移动.如果点P,Q同时出发,用t(s)表示移动的时间,那么当t=_________时,△POQ是等腰三角形.
第10题图 第11题图
11.如图,△ABC是等腰三角形,AB=AC,∠A=20°,BP平分∠ABC,D是射线BP上一点.如果点D满足△BCD是等腰三角形,那么∠BDC的度数是__________.
12.如图,在平面直角坐标系中,O为坐标原点,四边形OABC为长方形,点A,C的坐标分别为A(10,0),C(0,3),D是OA的中点,点P在边BC上运动.当△ODP是腰长为5的等腰三角形时,求点P的坐标.
参考答案
1.C. 2. 24
3.(1)设∠BAC=x°.4D=BD,∴∠BAC=∠ABD=x°.∴∠BDC=∠BAC+∠ABD=2x°.∵BD=BC,∴∠BDC=∠BCD=2x°,∵∴AB=AC,∴∠ABC=∠ACB=2x°.∵∠BAC+∠ABC+∠ACB=180°,∴x+2x+2x=180,解得x=36.∴∠BAC=36°,∠ACB=72°
(2)∵E是AB的中点,AD=BD,∴DE⊥AB,即FE⊥AB.∴AF=BF.∴∠BAF=∠ABF=72°.又∵∠ABD=∠BAD=36°,∴∠FAC=∠FBD=36°.∵∠ACB=72°,∴∠AFC=∠ACB-∠FAC=36°.∴∠FAC=∠AFC=36°.∴∠ACF是等腰三角形.
4. A 5. 6
6.(1)∵CD平分∠ACB,∴∠BCD=∠ACD.∵DE∥BC,∴∠EDC=∠BCD.∴∠EDC=∠ACD.∴ED=EC.∵E是边AC的中点,AC=8,∴∴DE=4
(2)∵DE∥BC,∴∠ADE=∠B,∠CDE=∠BCD.∵DE平分∠ADC,∴∠ADE=∠CDE.∴∠B=∠BCD.∴DB=DC.过点D作DG⊥BC于点G.∵DB=DC,DG⊥BC,∴ 5.∵∠B=30°,BF=DF,∴∠BDF=∠B=30°.∴∠DFG=∠B+∠BDF=60°.∴∠FDG=30°.∴BF=DF=2FG.∵GB=BF+FG=3FG=4.5,.∴FG=1.5.∴DF=2FG=3.
7.C
8.(1)△ABC是等腰三角形
(2)如图①,当点D在△ABC 内部时,(1)中的结论仍成立 理由:∵DE⊥AB,DF⊥AC,∴∠BED=∠CFD=90°.在Rt△DEB和Rt△DFC中,.∴Rt△DEB≌Rt△DFC.∴∠EBD=∠FCD.∵DB=DC,∴∠DBC=∠DCB.∴∠EBD+∠DBC=∠FCD+∠DCB,即∠EBC=∠FCB.∴AB=AC.∴△ABC是等腰三角形.
(3)当点D在∠ABC外部时,(1)中的结论不一定成立,反例不唯一,如图②所示
9.C 10. 或12 11.40°或70°或100°
12.过点P作PM⊥OA于点M,易得四边形OCPM为长方形.∵点A,C的坐标分别为(10,0),(0,3),∴OA=10,OC=3.∵D是OA的中点,∴
①当OP=OD时,OP=5,CO=3,∴易得CP=4.∴点P的坐标为(4,3).
②当OD=PD时,PD=5,PM=OC=3,∴易得MD=4.∴CP=5-4=1或CP=5+4=9.∴点P的坐标为(1,3)或(9,3).
综上所述,点P的坐标为(4,3)或(1,3)或(9,3).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专题训练
等腰三角形的性质与判定的综合应用
类型一 求角的度数
1.如图,在△ABC中,AB=AC,∠B=30°,D是AC的中点,过点D作DE⊥AC,交BC于点E,连接EA,则∠BAE的度数为 ( )
A.30° B.80° C.90° D.110°
第1题图 第2题图
2.如图,在△ABC中,∠BAC=108°,过点A作AD⊥BC于点D,且DC=AB+BD,则∠C=______°.
3.如图,在△ABC中,AB=AC,D为AC上一点,且满足AD=BD=BC.E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF.
(1)求∠BAC和∠ACB的度数;
(2)求证:△ACF是等腰三角形.
类型二 求线段的长度
4.如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD.若AC=6,BC=4,则BD的长为( )
A.1 B.1.5 C.2 D.2.5
5.如图,在△ABC中,ED∥BC,∠ABC和∠ACB 的平分线分别交ED于点G,F.若BE=6,DC=8,DE=20,则FG=_________.
6.已知在△ABC中,∠ACB的平分线CD交AB 于点D,DE∥BC.
(1)如图①,如果E是边AC的中点,AC=8,求:DE的长;
(2)如图②,DE平分∠ADC,∠B=30°,在边BC上取点F使BF=DF,若BC=9,求DF 的长.
类型三 判断三角形的形状
7.如图,在△ABC中,∠ABC=90°,∠C=30°,AD是∠BAC 的平分线,DE⊥AC于点E,AD,BE相交于点F,则图中的等腰三角形有( )
A.2个 B.3个 C.4个 D.5个
8.已知D为△ABC所在平面内一点,且DB=DC,DE⊥AB,DF⊥AC,垂足分别为E,F,DE=DF.
(1)如图,当点D在边BC上时,判断△ABC的形状(直接写出答案).
(2)当点D在△ABC内部时,(1)中的结论仍成立吗?若成立,请说明理由;若不成立,请举出反例(画图说明).
(3)当点D在△ABC外部时,(1)中的结论仍成立吗?若成立,请说明理由;若不成立,请举出反例(画图说明).
类型四 分类讨论思想的应用
9.已知一个等腰三角形一腰上的高与另一腰的夹角是50°,则这个等腰三角形的底角为( )
A.70° B.20° C.70°或20° D.40°或140°
10.如图,∠AOB=60°,C是BO延长线上的一点,OC=12cm,动点P从点C出发沿CB以3 cm/s的速度移动,动点Q从点O出发沿OA以2 cm/s的速度移动.如果点P,Q同时出发,用t(s)表示移动的时间,那么当t=_________时,△POQ是等腰三角形.
第10题图 第11题图
11.如图,△ABC是等腰三角形,AB=AC,∠A=20°,BP平分∠ABC,D是射线BP上一点.如果点D满足△BCD是等腰三角形,那么∠BDC的度数是__________.
12.如图,在平面直角坐标系中,O为坐标原点,四边形OABC为长方形,点A,C的坐标分别为A(10,0),C(0,3),D是OA的中点,点P在边BC上运动.当△ODP是腰长为5的等腰三角形时,求点P的坐标.
参考答案
1.C. 2. 24
3.(1)设∠BAC=x°.4D=BD,∴∠BAC=∠ABD=x°.∴∠BDC=∠BAC+∠ABD=2x°.∵BD=BC,∴∠BDC=∠BCD=2x°,∵∴AB=AC,∴∠ABC=∠ACB=2x°.∵∠BAC+∠ABC+∠ACB=180°,∴x+2x+2x=180,解得x=36.∴∠BAC=36°,∠ACB=72°
(2)∵E是AB的中点,AD=BD,∴DE⊥AB,即FE⊥AB.∴AF=BF.∴∠BAF=∠ABF=72°.又∵∠ABD=∠BAD=36°,∴∠FAC=∠FBD=36°.∵∠ACB=72°,∴∠AFC=∠ACB-∠FAC=36°.∴∠FAC=∠AFC=36°.∴∠ACF是等腰三角形.
4. A 5. 6
6.(1)∵CD平分∠ACB,∴∠BCD=∠ACD.∵DE∥BC,∴∠EDC=∠BCD.∴∠EDC=∠ACD.∴ED=EC.∵E是边AC的中点,AC=8,∴∴DE=4
(2)∵DE∥BC,∴∠ADE=∠B,∠CDE=∠BCD.∵DE平分∠ADC,∴∠ADE=∠CDE.∴∠B=∠BCD.∴DB=DC.过点D作DG⊥BC于点G.∵DB=DC,DG⊥BC,∴ 5.∵∠B=30°,BF=DF,∴∠BDF=∠B=30°.∴∠DFG=∠B+∠BDF=60°.∴∠FDG=30°.∴BF=DF=2FG.∵GB=BF+FG=3FG=4.5,.∴FG=1.5.∴DF=2FG=3.
7.C
8.(1)△ABC是等腰三角形
(2)如图①,当点D在△ABC 内部时,(1)中的结论仍成立 理由:∵DE⊥AB,DF⊥AC,∴∠BED=∠CFD=90°.在Rt△DEB和Rt△DFC中,.∴Rt△DEB≌Rt△DFC.∴∠EBD=∠FCD.∵DB=DC,∴∠DBC=∠DCB.∴∠EBD+∠DBC=∠FCD+∠DCB,即∠EBC=∠FCB.∴AB=AC.∴△ABC是等腰三角形.
(3)当点D在∠ABC外部时,(1)中的结论不一定成立,反例不唯一,如图②所示
9.C 10. 或12 11.40°或70°或100°
12.过点P作PM⊥OA于点M,易得四边形OCPM为长方形.∵点A,C的坐标分别为(10,0),(0,3),∴OA=10,OC=3.∵D是OA的中点,∴
①当OP=OD时,OP=5,CO=3,∴易得CP=4.∴点P的坐标为(4,3).
②当OD=PD时,PD=5,PM=OC=3,∴易得MD=4.∴CP=5-4=1或CP=5+4=9.∴点P的坐标为(1,3)或(9,3).
综上所述,点P的坐标为(4,3)或(1,3)或(9,3).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
