9.1.2不等式的基本性质
文档属性
| 名称 | 9.1.2不等式的基本性质 |  | |
| 格式 | zip | ||
| 文件大小 | 613.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-13 08:34:26 | ||
图片预览








文档简介
课件33张PPT。9.1.2 不等式的性质(1)观察:用“<”或“>”填空,并找一找其中的规律.(2) –1<3 -1+2____3+2
-1-3____3-36>4 6+2____4+2
6-2____4-2>><<发现:当不等式两边加上或减去同一个数时,不等号的方向________不变(3) 6>2 6×5____2×5
6 ÷ 2____ 2 ÷ 2(4) –2<3 (-2)×6____3×6
(-2)÷ 2 ____3 ÷ 2
当不等式的两边 乘以同一个正数时,不等号的方向______ . >><>不变 (2)观察:用“<”或“>”填空,并找一找其中的规律.(5) 6>2 6 x(- 2) ____ 2 x(- 2)
6 ÷(-2)____2 ÷(-2) (6) –2<4 (-2) x(- 2) ____ 4 x(-2)
(-2) ÷(-2)____4 ÷(-2) 当不等式的两边 除以同一个负数时,不等号的方向________. >< <> 改变(2)观察:用“<”或“>”填空,并找一找其中的规律.不等式性质1:
不等式两边加( 减去 )同一个正数,不等号的方向不变。
不等式性质2:
不等式两边乘( 或除以 )同一个正数,不等号的方向不变。
不等式性质3:
不等式两边乘( 或除以 )同一个负数,不等号的方向改变。
? 探究活动
比较等式与不等式的基本性质.
你可以用列表的方式进行对比.(请与你的伙伴交流)
这种解法对吗?如果正确,说出它根据的是不等式的哪一条基本性质;如果不正确,请就明理由。等式的性质判断(1)∵ a<b ∴ a-c <b-c
(2)∵ a<b ∴ a/3 <b/3
(3)∵ a<b ∴ -2a <-2b
(4)∵ -2a >0 ∴ a >0
(5)∵ -a <-3 ∴ a <3
设m>n,用“>”或“<”填空。 (1) m-5____ n-5
(2) m+4 ____ n+4
(3) 6m ____ 6n
(4) -3m ____ -3n试一试,看谁更快(1)若x+1>0,两边同加上-1,
得_________
(依据:_______________);
(2)若 x≤ ,两边同乘-3,
得 _________
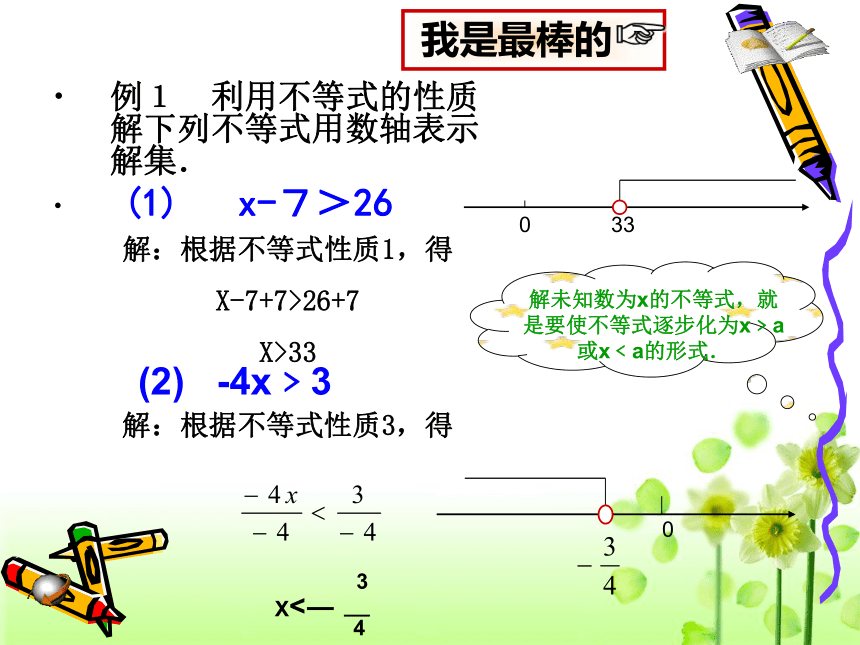
(依据:________________). x>-1不等式的基本性质2不等式的基本性质3填空:例1 利用不等式的性质解下列不等式用数轴表示解集.
(1) x-7>26解:根据不等式性质1,得
X-7+7>26+7
X>33(2) -4x﹥3 解:根据不等式性质3,得 (3) 3x<2x+1 3x-2x﹤2x+1-2x x﹤1这个不等式的解在数轴上的表示解:根据不等式性质1,得
x﹥75这个不等式的解集在数轴的表示如图解:根据不等式性质2,得
(1)X+5>- 1; (2)4X<3X-5;
(3) X < ; (4)-8X>10.1
76
7用不等式的性质解下列不等式,并在数轴上表示解集:感悟与反思 通过这节课的学习活动你有哪些收获?作业1、习题9.1第4、5、6、7题;
2、选作:习题9.1第8题。
利用不等式的性质解下列不等式
解:(1) x-7>26 (2) 3x<2x+1
(3)2/3x >50 (4)-4x >3
解决问题思考解:不等式两边同时乘以12,得
2(5x+1)-2×12>3(x-5)
10x+2-24>3x-15
10x-3x>24-2-15
7x>7
X>1试一试1.若-m>5,则m -5.
2.如果x/y>0, 那么xy 0.
3.如果a>-1,那么a-b -1-b.
A___>____m>><判断不等式的 性质1 不等式两边加(或减 )同 一个数(或式子),不等号的方向不变 。 不等式的 性质2 不等式两边乘(或除以)
同一个正数,不等号的方向不变 。
不等式的 性质3 不等式的两边 乘 (或除以)
同一个负数, 不等号的方向改变。
不等式的性质2 不等式的两边乘(或除以)同一个正数,不等号的方向不变. 如果a<b,c>0那么ac bc,字母表示为:﹤﹤ 不等式的性质1 不等式的两边加(或减)同一个数(或式子),不等号的方向不变.
如果a>b,那么a±c b±c
字母表示为:﹥ 不等式的性质 3 不等式的两边乘(或除以)同一个负数,不等号的方向改变
必须把不等号的方向改变如果a>b,c<0那么ac bc,字母表示为:类比推导﹤﹤例1 利用不等式的性质解下列不等式用数轴表示解集.
(1) x-7>26解:根据不等式性质1,得
X-7+7>26+7
X>33(2) -4x﹥3 解:根据不等式性质3,得0练习:利用不等式性质解不等式 (1)-2x>4 (2)3x<0解:(1)不等式的两边都除以-2,不等号的方向改变,所以
-2x÷(-2) < 4 ÷(-2) 得 x<-2
(2)不等式的两边都除以3,不等号的方向不改变,所以
3 x÷3<0÷3
得 x<0
x﹥75这个不等式的解集在数轴的表示如图自我检测利用不等式的性质解下列不等式用数轴表示解集.(1) x+3>-1解:根据不等式性质1,得
X<-7(3) 4x>-12解:根据不等式性质2,得
X>-3解:根据不等式性质1,得
X>-4(2) 6x<5x-7 不等式的 性质1 不等式两边加(或减 )同一个数(或式子),不等号的方向不变 。
不等式的 性质2 不等式两边乘(或除以)同一个正数,不等号的方向不变 。
不等式的 性质3 不等式的两边 乘 (或除以)同一个负数, 不等号的方向改变。
(3) 3x<2x+1 3x-2x﹤2x+1-2x x﹤1这个不等式的解在数轴上的表示注意:解不等式时也可以“移项”,即把不等式的一边的某项变号后移到另一边,而不改变不等号的方向.解:根据不等式性质1,得3x-2x﹤1 (3) 3x<2x+1 3x-2x﹤2x+1-2x x﹤1这个不等式的解在数轴上的表示解:根据不等式性质1,得3x-2x﹤1作业1、 课本P128 习题9.1 第6题
2、完成同步练习册再见
-1-3____3-36>4 6+2____4+2
6-2____4-2>><<发现:当不等式两边加上或减去同一个数时,不等号的方向________不变(3) 6>2 6×5____2×5
6 ÷ 2____ 2 ÷ 2(4) –2<3 (-2)×6____3×6
(-2)÷ 2 ____3 ÷ 2
当不等式的两边 乘以同一个正数时,不等号的方向______ . >><>不变 (2)观察:用“<”或“>”填空,并找一找其中的规律.(5) 6>2 6 x(- 2) ____ 2 x(- 2)
6 ÷(-2)____2 ÷(-2) (6) –2<4 (-2) x(- 2) ____ 4 x(-2)
(-2) ÷(-2)____4 ÷(-2) 当不等式的两边 除以同一个负数时,不等号的方向________. >< <> 改变(2)观察:用“<”或“>”填空,并找一找其中的规律.不等式性质1:
不等式两边加( 减去 )同一个正数,不等号的方向不变。
不等式性质2:
不等式两边乘( 或除以 )同一个正数,不等号的方向不变。
不等式性质3:
不等式两边乘( 或除以 )同一个负数,不等号的方向改变。
? 探究活动
比较等式与不等式的基本性质.
你可以用列表的方式进行对比.(请与你的伙伴交流)
这种解法对吗?如果正确,说出它根据的是不等式的哪一条基本性质;如果不正确,请就明理由。等式的性质判断(1)∵ a<b ∴ a-c <b-c
(2)∵ a<b ∴ a/3 <b/3
(3)∵ a<b ∴ -2a <-2b
(4)∵ -2a >0 ∴ a >0
(5)∵ -a <-3 ∴ a <3
设m>n,用“>”或“<”填空。 (1) m-5____ n-5
(2) m+4 ____ n+4
(3) 6m ____ 6n
(4) -3m ____ -3n试一试,看谁更快(1)若x+1>0,两边同加上-1,
得_________
(依据:_______________);
(2)若 x≤ ,两边同乘-3,
得 _________
(依据:________________). x>-1不等式的基本性质2不等式的基本性质3填空:例1 利用不等式的性质解下列不等式用数轴表示解集.
(1) x-7>26解:根据不等式性质1,得
X-7+7>26+7
X>33(2) -4x﹥3 解:根据不等式性质3,得 (3) 3x<2x+1 3x-2x﹤2x+1-2x x﹤1这个不等式的解在数轴上的表示解:根据不等式性质1,得
x﹥75这个不等式的解集在数轴的表示如图解:根据不等式性质2,得
(1)X+5>- 1; (2)4X<3X-5;
(3) X < ; (4)-8X>10.1
76
7用不等式的性质解下列不等式,并在数轴上表示解集:感悟与反思 通过这节课的学习活动你有哪些收获?作业1、习题9.1第4、5、6、7题;
2、选作:习题9.1第8题。
利用不等式的性质解下列不等式
解:(1) x-7>26 (2) 3x<2x+1
(3)2/3x >50 (4)-4x >3
解决问题思考解:不等式两边同时乘以12,得
2(5x+1)-2×12>3(x-5)
10x+2-24>3x-15
10x-3x>24-2-15
7x>7
X>1试一试1.若-m>5,则m -5.
2.如果x/y>0, 那么xy 0.
3.如果a>-1,那么a-b -1-b.
A___>____m>><判断不等式的 性质1 不等式两边加(或减 )同 一个数(或式子),不等号的方向不变 。 不等式的 性质2 不等式两边乘(或除以)
同一个正数,不等号的方向不变 。
不等式的 性质3 不等式的两边 乘 (或除以)
同一个负数, 不等号的方向改变。
不等式的性质2 不等式的两边乘(或除以)同一个正数,不等号的方向不变. 如果a<b,c>0那么ac bc,字母表示为:﹤﹤ 不等式的性质1 不等式的两边加(或减)同一个数(或式子),不等号的方向不变.
如果a>b,那么a±c b±c
字母表示为:﹥ 不等式的性质 3 不等式的两边乘(或除以)同一个负数,不等号的方向改变
必须把不等号的方向改变如果a>b,c<0那么ac bc,字母表示为:类比推导﹤﹤例1 利用不等式的性质解下列不等式用数轴表示解集.
(1) x-7>26解:根据不等式性质1,得
X-7+7>26+7
X>33(2) -4x﹥3 解:根据不等式性质3,得0练习:利用不等式性质解不等式 (1)-2x>4 (2)3x<0解:(1)不等式的两边都除以-2,不等号的方向改变,所以
-2x÷(-2) < 4 ÷(-2) 得 x<-2
(2)不等式的两边都除以3,不等号的方向不改变,所以
3 x÷3<0÷3
得 x<0
x﹥75这个不等式的解集在数轴的表示如图自我检测利用不等式的性质解下列不等式用数轴表示解集.(1) x+3>-1解:根据不等式性质1,得
X<-7(3) 4x>-12解:根据不等式性质2,得
X>-3解:根据不等式性质1,得
X>-4(2) 6x<5x-7 不等式的 性质1 不等式两边加(或减 )同一个数(或式子),不等号的方向不变 。
不等式的 性质2 不等式两边乘(或除以)同一个正数,不等号的方向不变 。
不等式的 性质3 不等式的两边 乘 (或除以)同一个负数, 不等号的方向改变。
(3) 3x<2x+1 3x-2x﹤2x+1-2x x﹤1这个不等式的解在数轴上的表示注意:解不等式时也可以“移项”,即把不等式的一边的某项变号后移到另一边,而不改变不等号的方向.解:根据不等式性质1,得3x-2x﹤1 (3) 3x<2x+1 3x-2x﹤2x+1-2x x﹤1这个不等式的解在数轴上的表示解:根据不等式性质1,得3x-2x﹤1作业1、 课本P128 习题9.1 第6题
2、完成同步练习册再见
