圆中一题多解训练
图片预览



文档简介
课件23张PPT。圆中一题多解
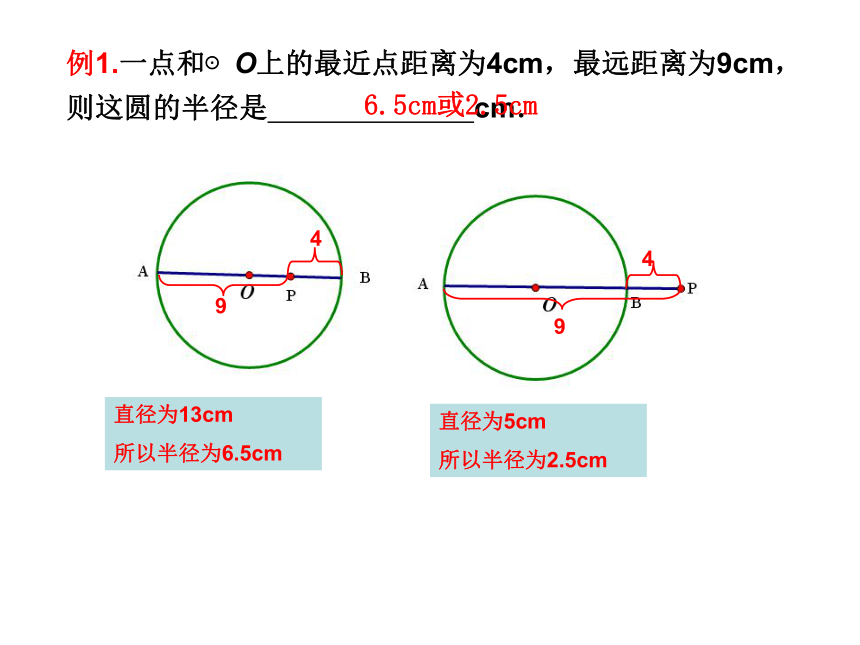
分析训练(一)例1.一点和⊙O上的最近点距离为4cm,最远距离为9cm,则这圆的半径是 cm.94直径为13cm
所以半径为6.5cm94直径为5cm
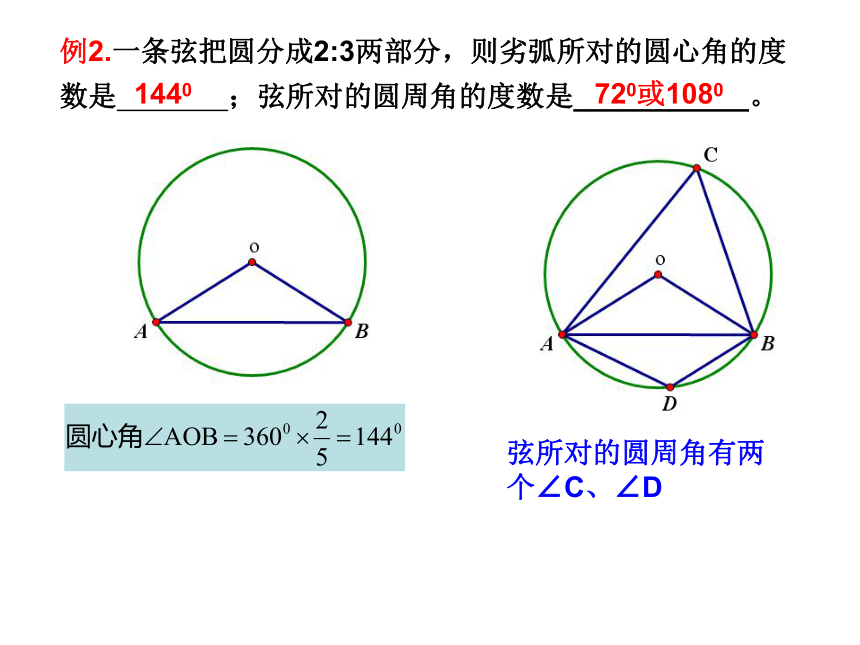
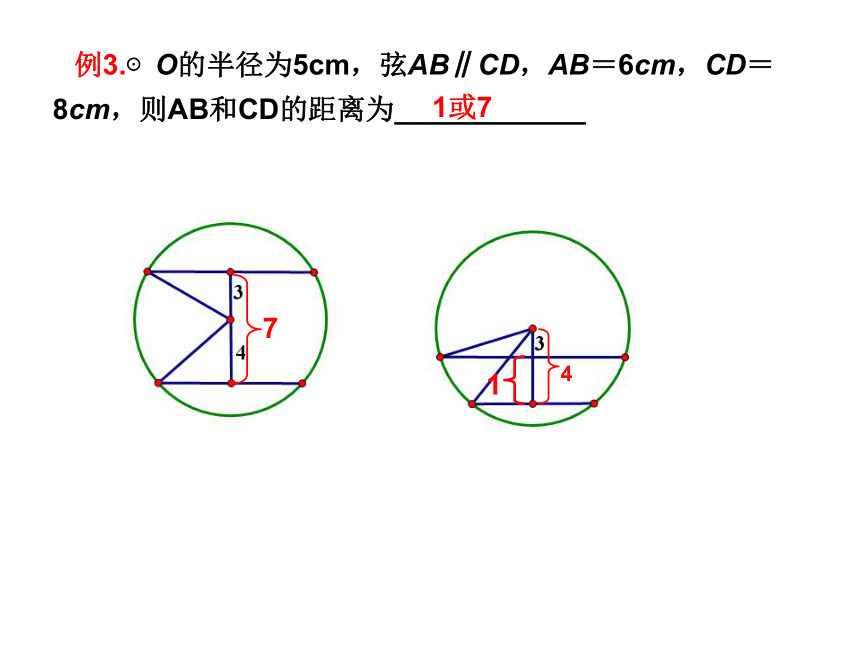
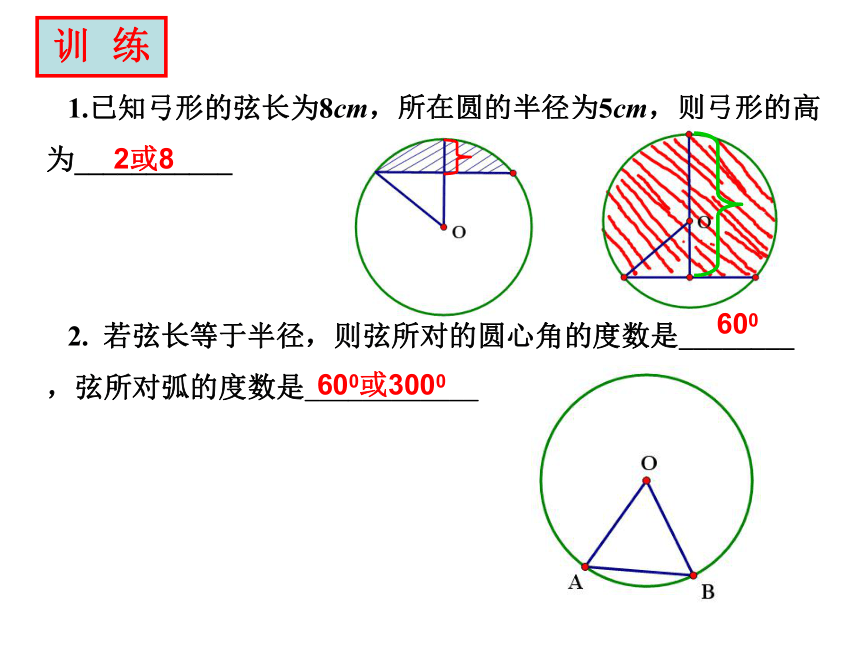
所以半径为2.5cm6.5cm或2.5cm例2.一条弦把圆分成2:3两部分,则劣弧所对的圆心角的度数是 ;弦所对的圆周角的度数是___________。1440弦所对的圆周角有两个∠C、∠D720或1080例3.⊙O的半径为5cm,弦AB∥CD,AB=6cm,CD=8cm,则AB和CD的距离为____________4711或71.已知弓形的弦长为8cm,所在圆的半径为5cm,则弓形的高为___________
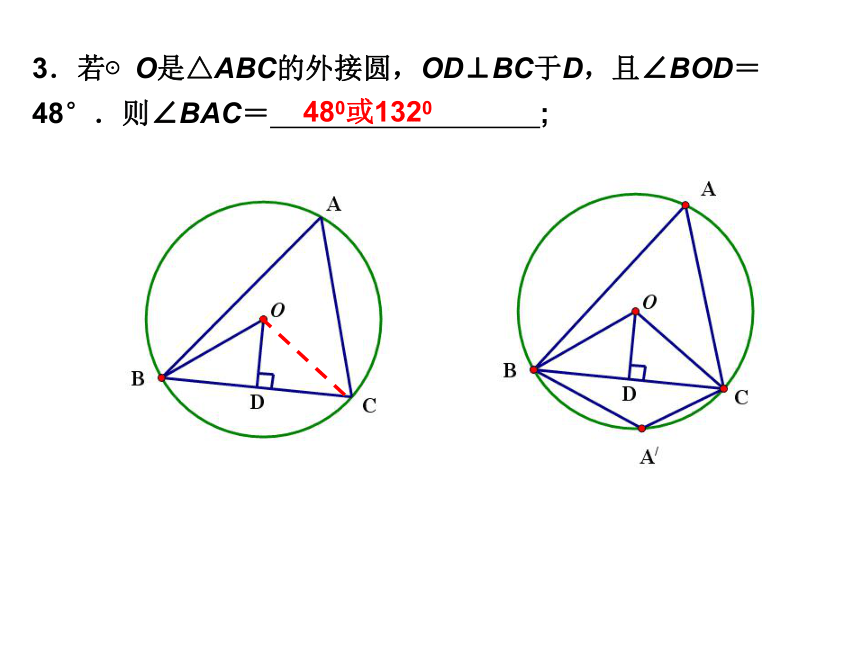
2. 若弦长等于半径,则弦所对的圆心角的度数是________,弦所对弧的度数是____________训 练2或8600600或30003.若⊙O是△ABC的外接圆,OD⊥BC于D,且∠BOD=48°.则∠BAC= ;480或1320600或1200圆中一题多解
分析训练(二)知识回顾:1、点与圆的位置关系有哪些? 2、直线与圆的位置关系有哪些? 3、圆与圆的位置关系有哪些? 正是这些与圆有关的位置关系的多样性引发了许多圆的双解问题。 例1 已知:在同一平面内,点P到⊙O上的点的最长距离为8cm,最短距离为2cm,则⊙O的半径为______.5cm或3cm 一、点与圆的位置关系不明确引发双解 凡涉及点与圆的位置关系问题,在没有指明其位置时,应考虑点在圆内、圆上、圆外三种可能情形。例2 已知:∠ABC=45°,点O为BC上的一点,且OB=6,若以点O为圆心,以r为半径的圆与射线BA只有一个公共点,则r的取值范围是 .二、直线与圆的位置关系不明确引发双解 凡涉及直线与圆的位置关系问题,在没有指明其位置时,应考虑直线圆相离、相切、相交三种可能情形。三、圆与圆的位置关系不明确引发双解1.由两圆相切的双重意义引发双解 例3 半径分别为3cm和5cm的两圆相切,则两圆圆心距为 cm. 两圆相切包括内切和外切。例4 已知:⊙O1的半径为2cm,⊙O2的半径为5cm,两圆没有公共点,则两圆的圆心距d的取值范围为___________ 两圆没有公共点,有外离和内含两种情况。0cm≤d<3cm 或d>7cm2.由两圆相离的双重意义引发双解 三、圆与圆的位置关系不明确引发双解例5 已知:⊙O1与⊙O2相交于A、B两点,⊙O1的半径为10,⊙O2的半径为17,公共弦AB=16,求两圆的圆心距.3.两圆相交公共弦与两圆心位置关系不明确引发双解三、圆与圆的位置关系不明确引发双解圆心与公共弦的位置关系有两种:
圆心在公共弦两侧;圆心在公共弦同侧。例6 已知:⊙O的半径为5cm,弦AB//CD,AB=6cm,CD=8cm.
求:AB与CD之间的距离. 1cm或7cm 四、两平行弦与圆心位置关系不明确引发双解两平行弦与圆心的位置关系一般有两种:
两弦在圆心的同侧;两弦在圆心的异侧。 例7 已知:⊙O的半径为1cm,弦则∠BAC=________ 15°或 75° 五、圆心与圆周角的位置关系不明确引发双解 圆心可能在圆周角内部,也可能在圆周角外部。 根据垂径定理及解直角三角形知识可求出∠CAO=45°和∠BAO=30°,从而可知∠BAC=15°或∠BAC=75°.例8 已知:△ABC内接于⊙O,∠AOB=100°,则∠ACB=______度 50°或130° 六、圆心与内接三角形位置关系不明确引发双解 圆心可能在三角形内部,也可能在三角形外部。 例9 圆的弦长恰好等于该圆的半径,则这条弦所对的圆周角是________度 30°或150° 七、由一弦对两弧引发双解A B弦AB所对的弧有优弧和劣弧两种 练习1 已知:⊙O的直径为6cm,如果直线a上的一点C到点O的距离为3cm,则直线a与⊙O的位置关系是_________ .相切或相交 直线与圆的位置关系不明确引发双解练习2 已知:PA,PC分别切⊙O于A、C两点,B为⊙O上与A,C不重合的点,若∠P=50°,则∠ABC=_____度.65°或115° 由一弦对两弧引发双解练习3 已知:矩形ABCD中,AB=5,BC=12,如果分别以A、C为圆心的两圆相切,点在圆内,点在圆外,那么圆的半径的取值范围是 . 题中未指明两圆是内切还是外切,故应对内(外)切分类讨论。小结: 回忆圆中哪些情况可能引发双解?本节课你还有什么收获?
分析训练(一)例1.一点和⊙O上的最近点距离为4cm,最远距离为9cm,则这圆的半径是 cm.94直径为13cm
所以半径为6.5cm94直径为5cm
所以半径为2.5cm6.5cm或2.5cm例2.一条弦把圆分成2:3两部分,则劣弧所对的圆心角的度数是 ;弦所对的圆周角的度数是___________。1440弦所对的圆周角有两个∠C、∠D720或1080例3.⊙O的半径为5cm,弦AB∥CD,AB=6cm,CD=8cm,则AB和CD的距离为____________4711或71.已知弓形的弦长为8cm,所在圆的半径为5cm,则弓形的高为___________
2. 若弦长等于半径,则弦所对的圆心角的度数是________,弦所对弧的度数是____________训 练2或8600600或30003.若⊙O是△ABC的外接圆,OD⊥BC于D,且∠BOD=48°.则∠BAC= ;480或1320600或1200圆中一题多解
分析训练(二)知识回顾:1、点与圆的位置关系有哪些? 2、直线与圆的位置关系有哪些? 3、圆与圆的位置关系有哪些? 正是这些与圆有关的位置关系的多样性引发了许多圆的双解问题。 例1 已知:在同一平面内,点P到⊙O上的点的最长距离为8cm,最短距离为2cm,则⊙O的半径为______.5cm或3cm 一、点与圆的位置关系不明确引发双解 凡涉及点与圆的位置关系问题,在没有指明其位置时,应考虑点在圆内、圆上、圆外三种可能情形。例2 已知:∠ABC=45°,点O为BC上的一点,且OB=6,若以点O为圆心,以r为半径的圆与射线BA只有一个公共点,则r的取值范围是 .二、直线与圆的位置关系不明确引发双解 凡涉及直线与圆的位置关系问题,在没有指明其位置时,应考虑直线圆相离、相切、相交三种可能情形。三、圆与圆的位置关系不明确引发双解1.由两圆相切的双重意义引发双解 例3 半径分别为3cm和5cm的两圆相切,则两圆圆心距为 cm. 两圆相切包括内切和外切。例4 已知:⊙O1的半径为2cm,⊙O2的半径为5cm,两圆没有公共点,则两圆的圆心距d的取值范围为___________ 两圆没有公共点,有外离和内含两种情况。0cm≤d<3cm 或d>7cm2.由两圆相离的双重意义引发双解 三、圆与圆的位置关系不明确引发双解例5 已知:⊙O1与⊙O2相交于A、B两点,⊙O1的半径为10,⊙O2的半径为17,公共弦AB=16,求两圆的圆心距.3.两圆相交公共弦与两圆心位置关系不明确引发双解三、圆与圆的位置关系不明确引发双解圆心与公共弦的位置关系有两种:
圆心在公共弦两侧;圆心在公共弦同侧。例6 已知:⊙O的半径为5cm,弦AB//CD,AB=6cm,CD=8cm.
求:AB与CD之间的距离. 1cm或7cm 四、两平行弦与圆心位置关系不明确引发双解两平行弦与圆心的位置关系一般有两种:
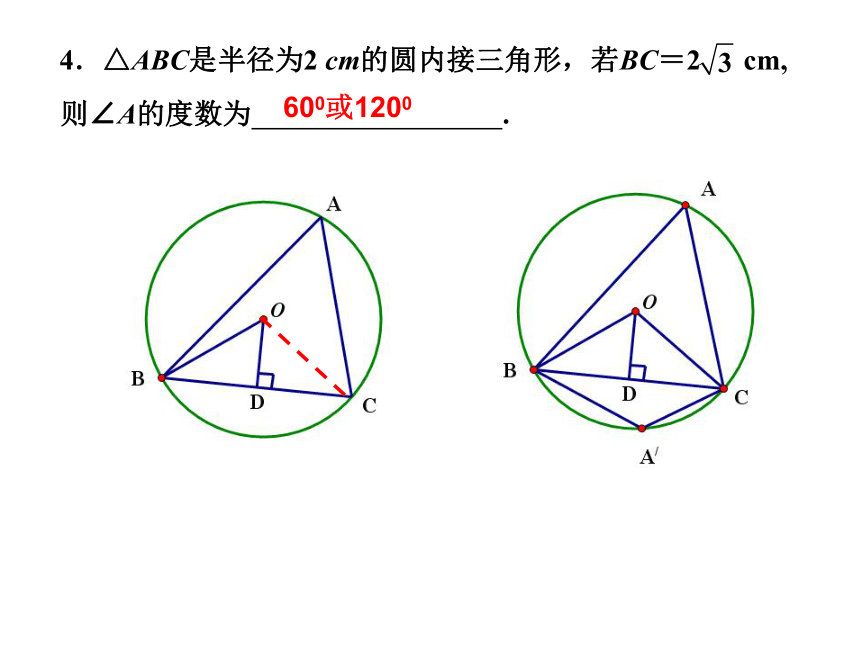
两弦在圆心的同侧;两弦在圆心的异侧。 例7 已知:⊙O的半径为1cm,弦则∠BAC=________ 15°或 75° 五、圆心与圆周角的位置关系不明确引发双解 圆心可能在圆周角内部,也可能在圆周角外部。 根据垂径定理及解直角三角形知识可求出∠CAO=45°和∠BAO=30°,从而可知∠BAC=15°或∠BAC=75°.例8 已知:△ABC内接于⊙O,∠AOB=100°,则∠ACB=______度 50°或130° 六、圆心与内接三角形位置关系不明确引发双解 圆心可能在三角形内部,也可能在三角形外部。 例9 圆的弦长恰好等于该圆的半径,则这条弦所对的圆周角是________度 30°或150° 七、由一弦对两弧引发双解A B弦AB所对的弧有优弧和劣弧两种 练习1 已知:⊙O的直径为6cm,如果直线a上的一点C到点O的距离为3cm,则直线a与⊙O的位置关系是_________ .相切或相交 直线与圆的位置关系不明确引发双解练习2 已知:PA,PC分别切⊙O于A、C两点,B为⊙O上与A,C不重合的点,若∠P=50°,则∠ABC=_____度.65°或115° 由一弦对两弧引发双解练习3 已知:矩形ABCD中,AB=5,BC=12,如果分别以A、C为圆心的两圆相切,点在圆内,点在圆外,那么圆的半径的取值范围是 . 题中未指明两圆是内切还是外切,故应对内(外)切分类讨论。小结: 回忆圆中哪些情况可能引发双解?本节课你还有什么收获?
