6.3一次函数的图象(2)

课件23张PPT。第六章 一次函数6.3 一次函数的图象(2)北师大版八年级数学（上册）复习旧知1、函数图象的定义： 把一个函数的自变量x与对应的因变量y的值
分别作为横坐标和纵坐标，在直角坐标系内描出
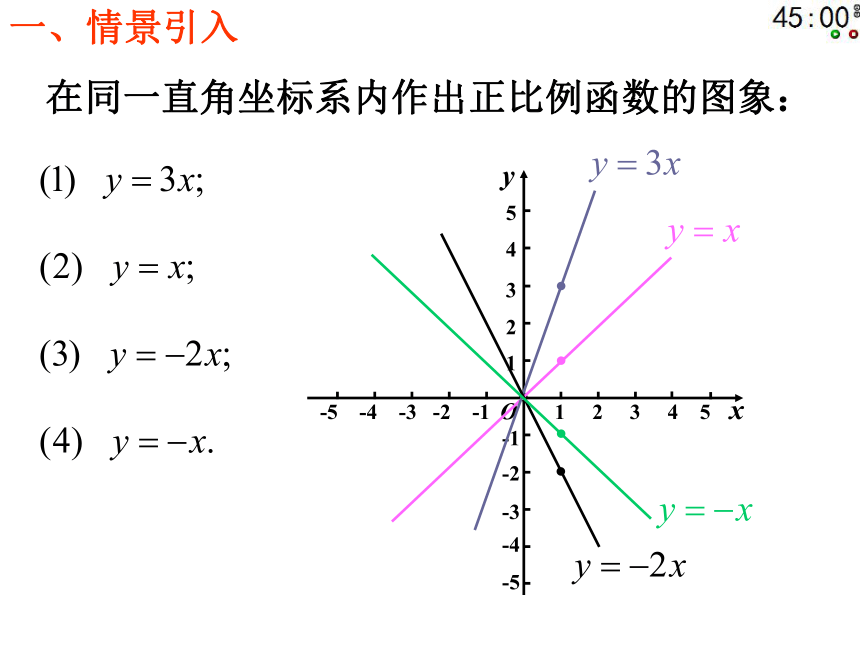
它的对应点，所得这些点组成的图形叫做该函数的图象。2、作函数图象的一般步骤：(1)列表：选择具有代表性的自变量的值和函数的对应值列成表格；(2)描点：将自变量的值作为横坐标，对应的函数值作为纵坐标，在坐标系中描出表格中的各点；(3)连线：按自变量从小到大的顺序，把所有点用平滑的曲线连接起来。复习旧知3、一次函数 的图象： 一次函数的图象是一条直线。4、一次函数 图象的画法： 用两点法画一次函数的图象。诊断练习1、在平面直角坐标系中作出函数的图象： 在同一直角坐标系内作出正比例函数的图象：一、情景引入二、学习目标1、会作正比例函数的图象。
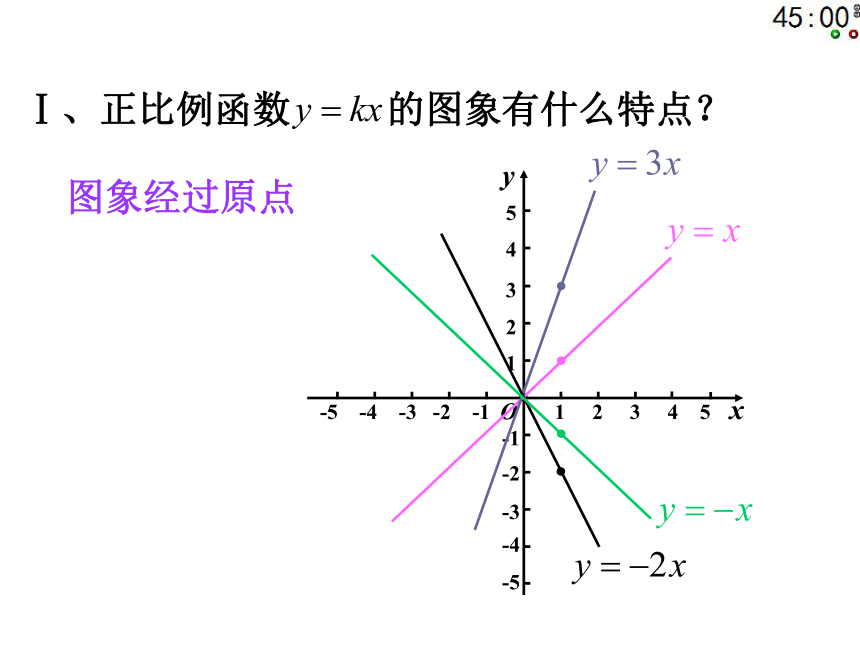
2、理解一次函数及其图象的有关性质。 Ⅰ、正比例函数 的图象有什么特点？图象经过原点新知归纳正比例函数 的图象： 正比例函数 的图象是经过原点(0, 0)
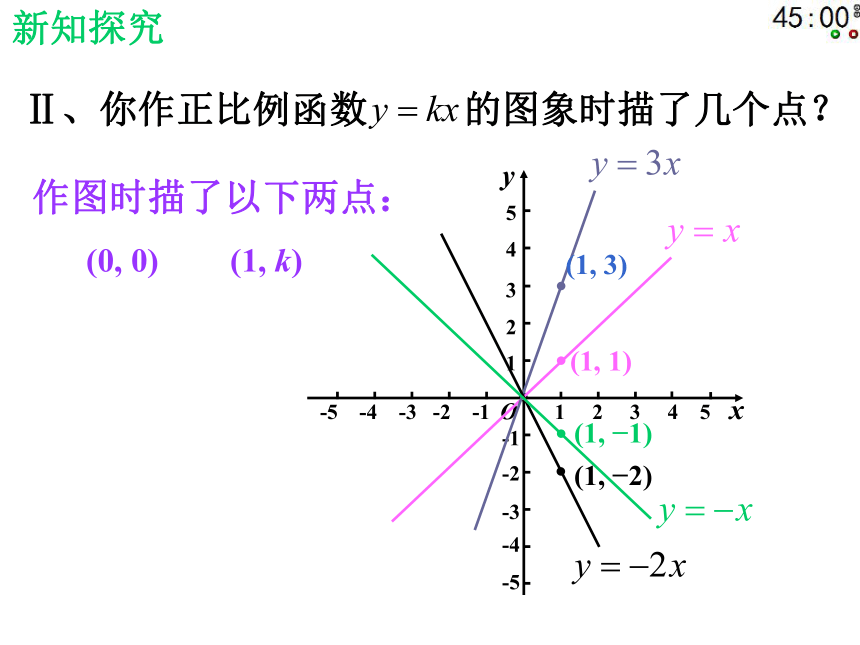
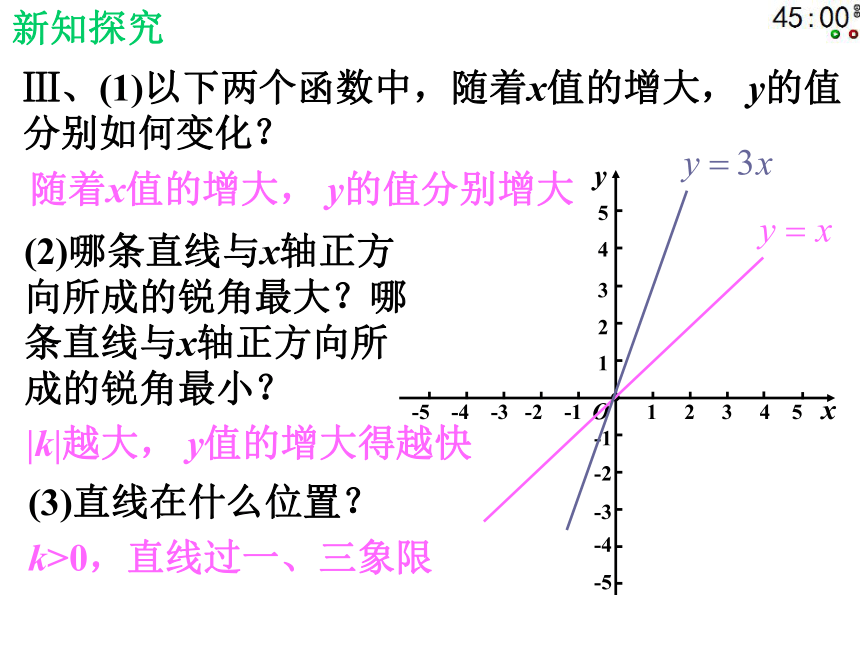
的一条直线。Ⅱ、你作正比例函数 的图象时描了几个点？新知探究(1, 3)(1, 1)(1, ?2)(1, ?1)(0, 0)(1, k)作图时描了以下两点：Ⅲ、(1)以下两个函数中，随着x值的增大， y的值分别如何变化？新知探究(2)哪条直线与x轴正方
向所成的锐角最大？哪
条直线与x轴正方向所
成的锐角最小？随着x值的增大， y的值分别增大|k|越大， y值的增大得越快(3)直线在什么位置？k>0，直线过一、三象限新知归纳正比例函数 的性质：(1)当k>0时，直线经过一、三象限，y的值随x值的增大而增大；Ⅲ、(1)以下两个函数中，随着x值的增大， y的值分别如何变化？新知探究(2)哪条直线与x轴正方
向所成的锐角最大？哪
条直线与x轴正方向所
成的锐角最小？随着x值的增大， y的值分别减小|k|越大， y值的减小得越快(3)直线在什么位置？k<0，直线过二、四象限新知归纳正比例例函数 的性质：(1)当k>0时，直线经过一、三象限，y的值随x值的增大而增大；(2)当k<0时，直线经过二、四象限，y的值随x值的增大而减小。1、函数 中，y的值随x值的增大而 。巩固练习2、下列一次函数中，y的值随x值的增大而减小
的有 。合作交流ⅰ、在同一直角坐标系内分别作出一次函数的图
象：合作交流ⅱ、(1)这三条直线有什么关系？k值相等，直线互相平行(2)这三条直线是通过怎样
的变换而相互得到的？b>0，向上平移|b|个单位b<0，向下平移|b|个单位(3)这三条直线分别在什
么位置？新知归纳一次例函数 的性质：(1)k>0，y的值随x值的增大而增大①b>0时，直线经过一、三、二象限；②b<0时，直线经过一、三、四象限。3、在同一直角坐标系内作出下列函数的图象：巩固练习新知归纳一次例函数 的性质：(1)k>0，y的值随x值的增大而增大(2)当k<0时，y的值随x值的增大而减小①b>0时，直线经过一、三、二象限；②b<0时，直线经过一、三、四象限。①b>0时，直线经过二、四、一象限；②b<0时，直线经过二、四、三象限。K>ob=0b>0b<0b=0b>0b<0通过作以上一次函数的图像我们发现y=kx+b
中，k,b的取值跟图像的关系如下：K<0一，三一，二，三一，三，四二，四一，二，四二，三，四当k>0时，y的值随x的增大而增大当k<0时，y的值随x的增大而减小4、x从0开始逐渐增大时， 和 哪一
个的值先达到20？这说明了什么？巩固练习5、在同一直角坐标系内作出下列函数的图象：巩固练习6、写出图中直线l所表示的变量x、y之间的关系式。7、写出m的3个值，使相应的一次函数
的值都是随着x的增大而减小。
由此你能想到什么？【达标检测】 1.下列一次函数中，y的值随x的增大而减小的有_______。(2) (4)(1) y=10x-9(2) y=-0.3x+22.下列哪个图像是一次函数y=-3x+5和y=2x-4的大致图像（　　）Ｂ3.如果一次函数y=kx－3k+6的图象经过原点，那么k的值为_______。4.写出m的3个值，使相应的一次函数y = (2m－1)x+2的值都是随x的增大而减小．Ｋ＝２可以写无数个，只要满足２ｍ－１＜０就可以了。
例如：ｍ＝０．ｍ＝－１，ｍ＝－２课堂小结1、正比例函数 的图象： 正比例函数 的图象是经过原点(0, 0)
的一条直线。2、一次例函数 的性质：(1)当k>0时，y的值随x值的增大而增大；(2)当k<0时，y的值随x值的增大而减小。