人教版2021--2022八年级(下)数学第十八单元质量检测试卷B(含解析)
文档属性
| 名称 | 人教版2021--2022八年级(下)数学第十八单元质量检测试卷B(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-27 14:27:58 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版2021-2022学年八年级(下)第十八章平行四边形检测试卷B
(时间120分钟,满分120分)
一、选择题(共10小题;每小题3分,共30分)
1. 工人师傅在做门窗或矩形零件时,不仅要测量两组对边的长度是否分别相等,常常还要测量它们的两条对角线是否相等,以确保图形是矩形.这样做的道理是
A. 两组对边分别相等的四边形是矩形
B. 有一个角是直角的平行四边形是矩形
C. 对角线相等的四边形是矩形
D. 对角线相等的平行四边形是矩形
2. 如图,直线 , 为 上一点, 为 上一点,以点 为圆心, 的长为半径画弧,与 相交于点 ,连接 .若以点 为圆心, 的长为半径画弧,与 相交于点 ,则四边形 不可能是
A. 平行四边形 B. 梯形 C. 菱形 D. 正方形
3. 梯形的对角线互相垂直,其中一条对角线长是 厘米,另一条对角线等于 厘米,那么这个梯形的面积是
A. B. C. D.
4. 下列命题正确的是
A. 对角线互相平分的四边形是菱形
B. 对角线互相平分且相等的四边形是菱形
C. 对角线互相垂直且相等的四边形是菱形
D. 对角线互相垂直且平分的四边形是菱形
5. 矩形具有而菱形不一定具有的的性质是
A. 四条边都相等 B. 对角线平分每一组对角
C. 两条对角线互相垂直 D. 两条对角线相等
6. 下列条件可以利用定义说明平行四边形 是正方形的是
A. , B. ,
C. , D. 以上均错
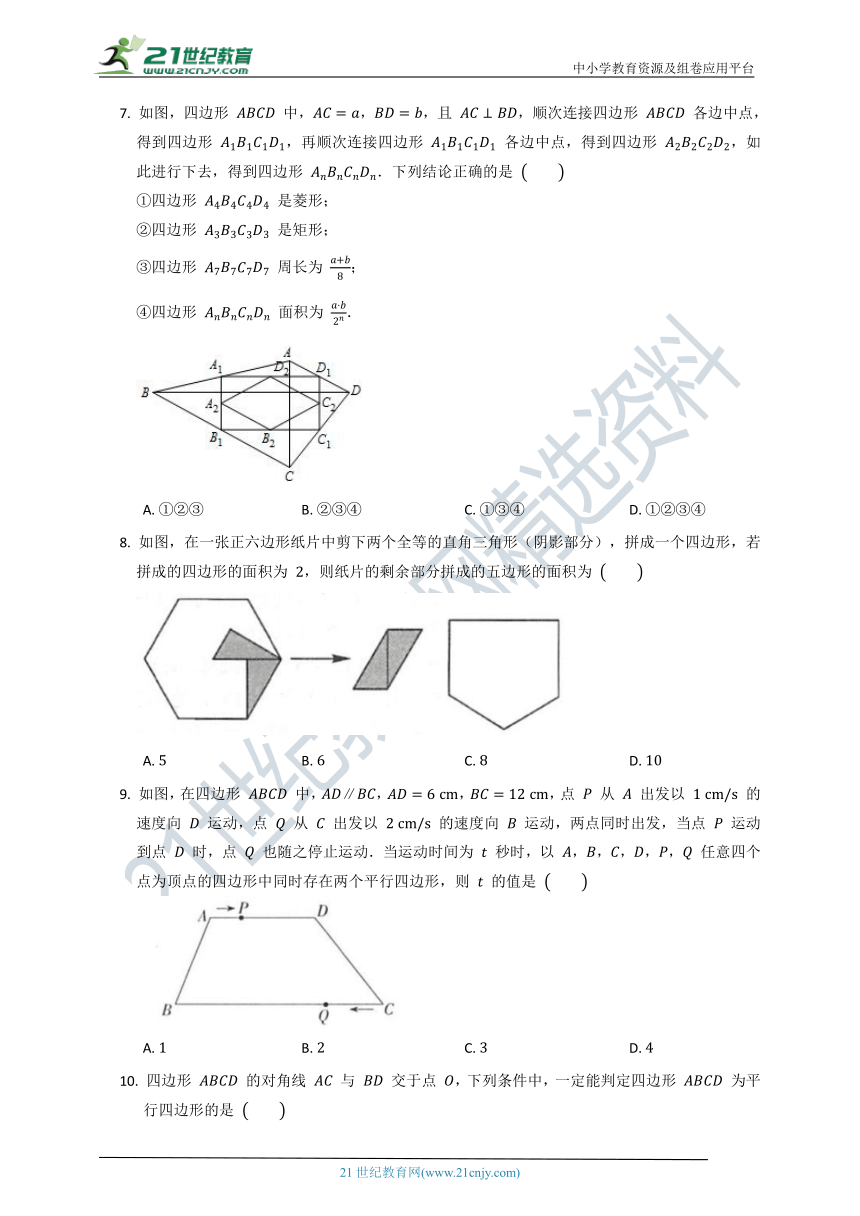
7. 如图,四边形 中,,,且 ,顺次连接四边形 各边中点,得到四边形 ,再顺次连接四边形 各边中点,得到四边形 ,如此进行下去,得到四边形 .下列结论正确的是
①四边形 是菱形;
②四边形 是矩形;
③四边形 周长为 ;
④四边形 面积为 .
A. ①②③ B. ②③④ C. ①③④ D. ①②③④
8. 如图,在一张正六边形纸片中剪下两个全等的直角三角形(阴影部分),拼成一个四边形,若拼成的四边形的面积为 ,则纸片的剩余部分拼成的五边形的面积为
A. B. C. D.
9. 如图,在四边形 中,,,,点 从 出发以 的速度向 运动,点 从 出发以 的速度向 运动,两点同时出发,当点 运动到点 时,点 也随之停止运动.当运动时间为 秒时,以 ,,,,, 任意四个点为顶点的四边形中同时存在两个平行四边形,则 的值是
A. B. C. D.
10. 四边形 的对角线 与 交于点 ,下列条件中,一定能判定四边形 为平行四边形的是
A. B.
C. , D. ,
二、填空题(共6小题;每小题3分,共18分)
11. 矩形的定义
有一个角是 的平行四边形叫做矩形.
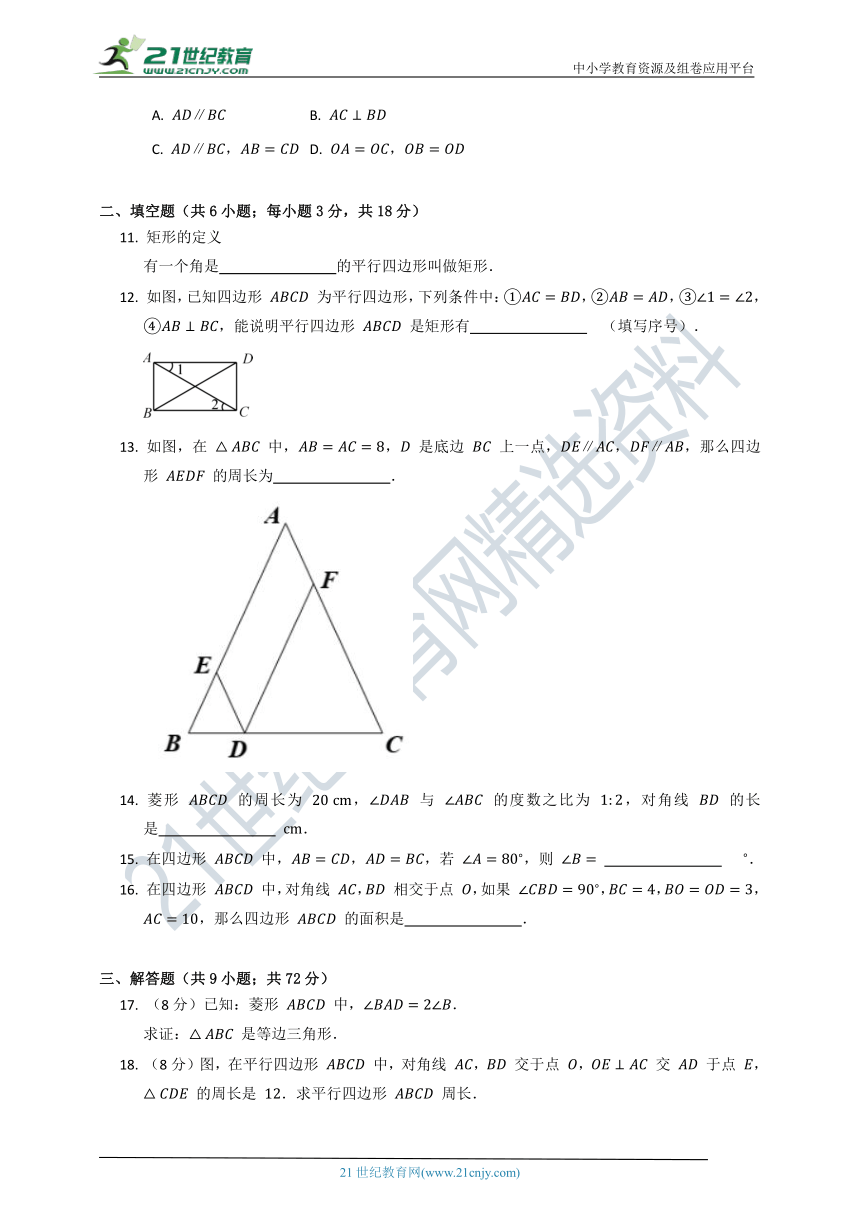
12. 如图,已知四边形 为平行四边形,下列条件中:,,,,能说明平行四边形 是矩形有 (填写序号).
13. 如图,在 中,, 是底边 上一点,,,那么四边形 的周长为 .
14. 菱形 的周长为 , 与 的度数之比为 ,对角线 的长是 .
15. 在四边形 中,,,若 ,则 .
16. 在四边形 中,对角线 , 相交于点 ,如果 ,,,,那么四边形 的面积是 .
三、解答题(共9小题;共72分)
17. (8分)已知:菱形 中,.
求证: 是等边三角形.
18. (8分)图,在平行四边形 中,对角线 , 交于点 , 交 于点 , 的周长是 .求平行四边形 周长.
19. (8分)如图,已知直角梯形 中,,,,,,,垂足为点 .求 的长.
20(8分)已知:如图,在 中,点 ,, 分别为 ,, 上的点,,且 ,延长 到点 ,使 .
求证:, 互相平分.
21. (8分)如图,在梯形 中,,,,,求 的长.
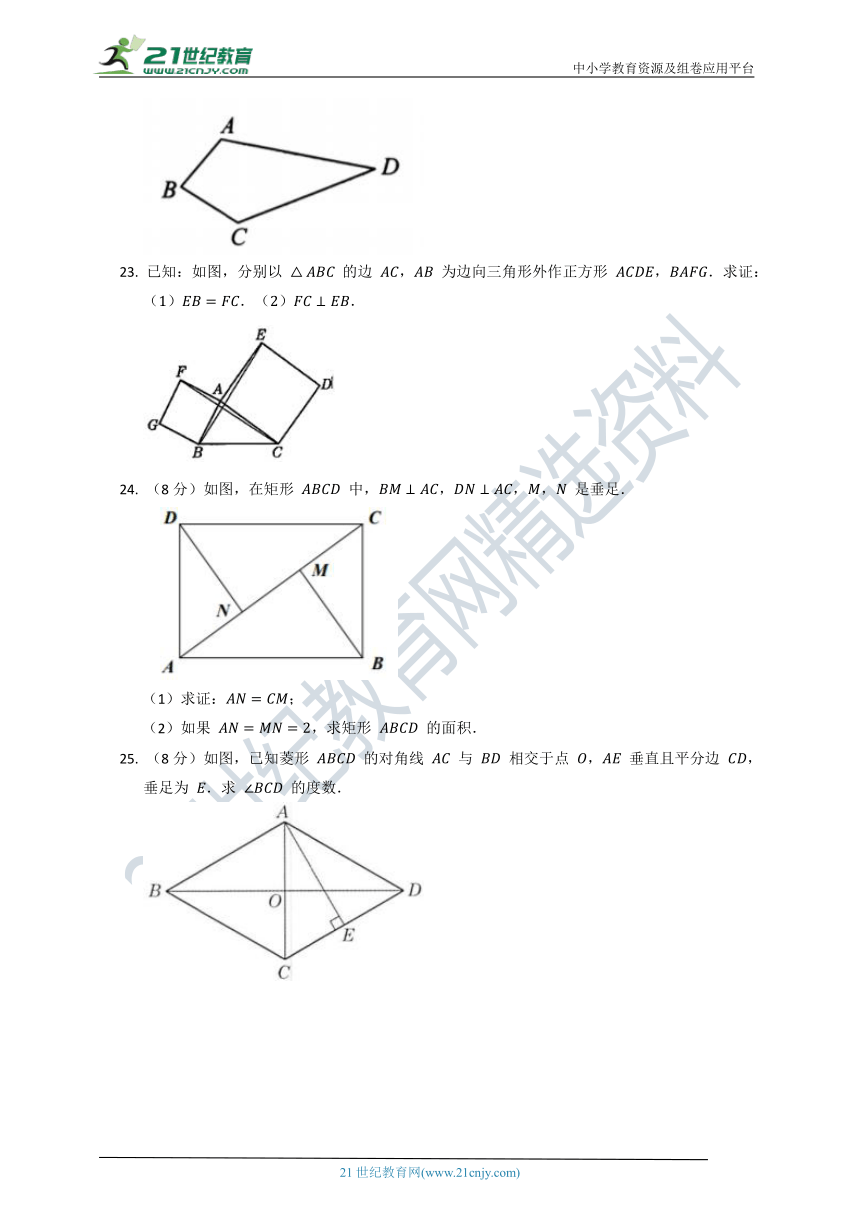
22. (8分)如图所示,田村有一口呈四边形的池塘,在它的四个角 ,,, 处均种有一棵大核桃树,田村准备开挖池塘建养鱼池,想使池塘面积扩大一倍,又想保持核桃树不动,并要求扩建后的池塘成平行四边形形状,请问田村能否实现这一设想 若能,请你设计并画出图形;若不能,请说明理由(画图要保留痕迹,不写画法).
23. 已知:如图,分别以 的边 , 为边向三角形外作正方形 ,.求证:().().
24. (8分)如图,在矩形 中,,,, 是垂足.
(1)求证:;
(2)如果 ,求矩形 的面积.
25. (8分)如图,已知菱形 的对角线 与 相交于点 , 垂直且平分边 ,垂足为 .求 的度数.
答案
第一部分
1. D 【解析】 两组对边的长度分别相等,,,
四边形 为平行四边形,
又 测量它们的两条对角线相等,,
平行四边形 为矩形.
2. D
3. B 【解析】梯形的面积为两互相垂直的对角线的积的一半,所以梯形面积为:.
4. D
5. D
6. B 【解析】正方形定义中需要的条件是一个角是直角,一组邻边相等的平行四边形,符合这一条件的只有选项B.
7. A 【解析】 四边形 是矩形,四边形 是菱形,
四边形 ,当 为奇数时,四边形为矩形;当 为偶数时,四边形为菱形.
四边形 的周长是 ,四边形 的周长是 ,四边形 的周长是 ,四边形 的周长是 .
四边形 的面积是 ,四边形 的面积是 ,四边形 的面积是 ,,四边形 的面积是 .
8. D
9. C 【解析】A. 时,,,,,此时不能构成平行四边形,不符合题意;
B. 时,,,,,此时只构成一个平行四边形,即平行四边形 ,不符合题意;
C. 时,,,则 ,此时存在两个平行四边形:平行四边形 和平行四边形 ,符合题意;
D. 时,,,,,此时只构成一个平行四边形,即平行四边形 ,不符合题意.
10. D
【解析】根据对角线互相平分的四边形是平行四边形,可以判断选项D正确.
第二部分
11. 直角
12. ①④
13.
14.
15.
【解析】,,
四边形 是平行四边形,
,
,
又 ,
.
16.
第三部分
17. 由 ,且 ,可得 ,
又 ,
所以 是等边三角形.
18. 关键: 垂直平分 , 的周长 ,所以平行四边形 的周长为 .
19. 提示:用两种不同的方法表示 ,可得 ,
的长是 .
20. 提示:先证 且 ,再证 且 ,推出四边形 为平行四边形,从而 , 互相平分.
21. .
22. 能实现这一设想,如图所示.
理由:
,,,,
即四边形 的面积为四边形 面积的 倍.
23. 提示:证明 .
24. (1) .
(2) 连接 交 于点 ,易得 ,,那么 , 的面积为 ,矩形面积为 .
25. 由条件可推出 ,即 , 都是等边三角形,于是可得 .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版2021-2022学年八年级(下)第十八章平行四边形检测试卷B
(时间120分钟,满分120分)
一、选择题(共10小题;每小题3分,共30分)
1. 工人师傅在做门窗或矩形零件时,不仅要测量两组对边的长度是否分别相等,常常还要测量它们的两条对角线是否相等,以确保图形是矩形.这样做的道理是
A. 两组对边分别相等的四边形是矩形
B. 有一个角是直角的平行四边形是矩形
C. 对角线相等的四边形是矩形
D. 对角线相等的平行四边形是矩形
2. 如图,直线 , 为 上一点, 为 上一点,以点 为圆心, 的长为半径画弧,与 相交于点 ,连接 .若以点 为圆心, 的长为半径画弧,与 相交于点 ,则四边形 不可能是
A. 平行四边形 B. 梯形 C. 菱形 D. 正方形
3. 梯形的对角线互相垂直,其中一条对角线长是 厘米,另一条对角线等于 厘米,那么这个梯形的面积是
A. B. C. D.
4. 下列命题正确的是
A. 对角线互相平分的四边形是菱形
B. 对角线互相平分且相等的四边形是菱形
C. 对角线互相垂直且相等的四边形是菱形
D. 对角线互相垂直且平分的四边形是菱形
5. 矩形具有而菱形不一定具有的的性质是
A. 四条边都相等 B. 对角线平分每一组对角
C. 两条对角线互相垂直 D. 两条对角线相等
6. 下列条件可以利用定义说明平行四边形 是正方形的是
A. , B. ,
C. , D. 以上均错
7. 如图,四边形 中,,,且 ,顺次连接四边形 各边中点,得到四边形 ,再顺次连接四边形 各边中点,得到四边形 ,如此进行下去,得到四边形 .下列结论正确的是
①四边形 是菱形;
②四边形 是矩形;
③四边形 周长为 ;
④四边形 面积为 .
A. ①②③ B. ②③④ C. ①③④ D. ①②③④
8. 如图,在一张正六边形纸片中剪下两个全等的直角三角形(阴影部分),拼成一个四边形,若拼成的四边形的面积为 ,则纸片的剩余部分拼成的五边形的面积为
A. B. C. D.
9. 如图,在四边形 中,,,,点 从 出发以 的速度向 运动,点 从 出发以 的速度向 运动,两点同时出发,当点 运动到点 时,点 也随之停止运动.当运动时间为 秒时,以 ,,,,, 任意四个点为顶点的四边形中同时存在两个平行四边形,则 的值是
A. B. C. D.
10. 四边形 的对角线 与 交于点 ,下列条件中,一定能判定四边形 为平行四边形的是
A. B.
C. , D. ,
二、填空题(共6小题;每小题3分,共18分)
11. 矩形的定义
有一个角是 的平行四边形叫做矩形.
12. 如图,已知四边形 为平行四边形,下列条件中:,,,,能说明平行四边形 是矩形有 (填写序号).
13. 如图,在 中,, 是底边 上一点,,,那么四边形 的周长为 .
14. 菱形 的周长为 , 与 的度数之比为 ,对角线 的长是 .
15. 在四边形 中,,,若 ,则 .
16. 在四边形 中,对角线 , 相交于点 ,如果 ,,,,那么四边形 的面积是 .
三、解答题(共9小题;共72分)
17. (8分)已知:菱形 中,.
求证: 是等边三角形.
18. (8分)图,在平行四边形 中,对角线 , 交于点 , 交 于点 , 的周长是 .求平行四边形 周长.
19. (8分)如图,已知直角梯形 中,,,,,,,垂足为点 .求 的长.
20(8分)已知:如图,在 中,点 ,, 分别为 ,, 上的点,,且 ,延长 到点 ,使 .
求证:, 互相平分.
21. (8分)如图,在梯形 中,,,,,求 的长.
22. (8分)如图所示,田村有一口呈四边形的池塘,在它的四个角 ,,, 处均种有一棵大核桃树,田村准备开挖池塘建养鱼池,想使池塘面积扩大一倍,又想保持核桃树不动,并要求扩建后的池塘成平行四边形形状,请问田村能否实现这一设想 若能,请你设计并画出图形;若不能,请说明理由(画图要保留痕迹,不写画法).
23. 已知:如图,分别以 的边 , 为边向三角形外作正方形 ,.求证:().().
24. (8分)如图,在矩形 中,,,, 是垂足.
(1)求证:;
(2)如果 ,求矩形 的面积.
25. (8分)如图,已知菱形 的对角线 与 相交于点 , 垂直且平分边 ,垂足为 .求 的度数.
答案
第一部分
1. D 【解析】 两组对边的长度分别相等,,,
四边形 为平行四边形,
又 测量它们的两条对角线相等,,
平行四边形 为矩形.
2. D
3. B 【解析】梯形的面积为两互相垂直的对角线的积的一半,所以梯形面积为:.
4. D
5. D
6. B 【解析】正方形定义中需要的条件是一个角是直角,一组邻边相等的平行四边形,符合这一条件的只有选项B.
7. A 【解析】 四边形 是矩形,四边形 是菱形,
四边形 ,当 为奇数时,四边形为矩形;当 为偶数时,四边形为菱形.
四边形 的周长是 ,四边形 的周长是 ,四边形 的周长是 ,四边形 的周长是 .
四边形 的面积是 ,四边形 的面积是 ,四边形 的面积是 ,,四边形 的面积是 .
8. D
9. C 【解析】A. 时,,,,,此时不能构成平行四边形,不符合题意;
B. 时,,,,,此时只构成一个平行四边形,即平行四边形 ,不符合题意;
C. 时,,,则 ,此时存在两个平行四边形:平行四边形 和平行四边形 ,符合题意;
D. 时,,,,,此时只构成一个平行四边形,即平行四边形 ,不符合题意.
10. D
【解析】根据对角线互相平分的四边形是平行四边形,可以判断选项D正确.
第二部分
11. 直角
12. ①④
13.
14.
15.
【解析】,,
四边形 是平行四边形,
,
,
又 ,
.
16.
第三部分
17. 由 ,且 ,可得 ,
又 ,
所以 是等边三角形.
18. 关键: 垂直平分 , 的周长 ,所以平行四边形 的周长为 .
19. 提示:用两种不同的方法表示 ,可得 ,
的长是 .
20. 提示:先证 且 ,再证 且 ,推出四边形 为平行四边形,从而 , 互相平分.
21. .
22. 能实现这一设想,如图所示.
理由:
,,,,
即四边形 的面积为四边形 面积的 倍.
23. 提示:证明 .
24. (1) .
(2) 连接 交 于点 ,易得 ,,那么 , 的面积为 ,矩形面积为 .
25. 由条件可推出 ,即 , 都是等边三角形,于是可得 .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
