人教版2021--2022八年级(下)数学第十八单元质量检测试卷C(含解析)
文档属性
| 名称 | 人教版2021--2022八年级(下)数学第十八单元质量检测试卷C(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-27 14:27:15 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版2021-2022学年八年级(下)第十八章平行四边形检测试卷C
(时间120分钟,满分120分)
一、选择题(共10小题;每小题3分,共30分)
1. 如图,在四边形 中,,,若 ,则 的度数为
A. B. C. D.
2. 下列说法正确的是
A. 一组对边平行的四边形是梯形
B. 一组对边平行且相等的四边形是梯形
C. 一组对边平行且不相等的四边形是梯形
D. 只有一组对边相等的四边形是梯形
3. 下列结论正确的是
A. 邻角相等的四边形是菱形
B. 有一组邻边相等的四边形是菱形
C. 对角线互相垂直的四边形是菱形
D. 对角线互相垂直平分的四边形是菱形
4. 下列条件不能判定四边形 是平行四边形的是
A. , B. ,
C. , D. ,
5. 下列条件中,能判定平行四边形 是菱形的是
A. B. C. D.
6. 如图,要测定被池塘隔开的 , 两点的距离,可以在 外选一点 ,连接 ,,并分别找出它们的中点 ,,连接 .现测得 ,,,则
A. B. C. D.
7. 已知:梯形的四边分别为 ,,,,则这个梯形的面积是
A. B. C. D.
8. 如图,已知直线 ,小王在直线 上任取 个点:,,,,,经测量发现它们到直线 的距离都是 ;小丁在直线 上任取 个点:,,,,,经测量发现它们到直线 的距离 也都是 .该操作反映了平行线的某种性质,下列对该性质的描述中,不正确的是
A. 如果直线 ,那么直线 上任意一点到直线 的距离都相等
B. 如果直线 ,那么直线 上任意一点到直线 的距离都相等
C. 两条平行线中,任意一条直线上的所有点到另一条直线的距离是一个定值
D. 两条平行线中,一条直线上的任意一点与另一条直线上的任意一点之间的距离都是一个定值
9. 如图所示,在矩形 中,,,两条对角线相交于点 .以 , 为邻边作第 个平行四边形 ,对角线相交于点 ;再以 , 为邻边作第 平行四边形个 ,对角线相交于点 ;再以 , 为邻边作第 个平行四边形 ;,依此类推,第 个平行四边形的面积为
A. B. C. D.
10. 如图,在梯形 中,,连接 , 交于 点,则图中面积相等的三角形共有
A. 对 B. 对 C. 对 D. 对
二、填空题(共6小题;每小题3分,共18分)
11. 小敏不慎将一块平行四边形玻璃打碎成如图所示的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带来了两块碎玻璃,其编号应该是 .
12. 有一个角是 的平行四边形是矩形.
13. 在四边形 中,如果 且 ,,那么 .
14. 请完善本课时知识结构图
15. 将正方形纸片以适当的方式折叠一次,沿折痕剪开后得到两块小纸片,用这两块小纸片拼接成一个新的多边形(不重叠、无缝隙),给出以下结论:
①可以拼成等腰直角三角形;
②可以拼成对角互补的四边形;
③可以拼成五边形;
④可以拼成六边形.
其中所有正确结论的序号是 .
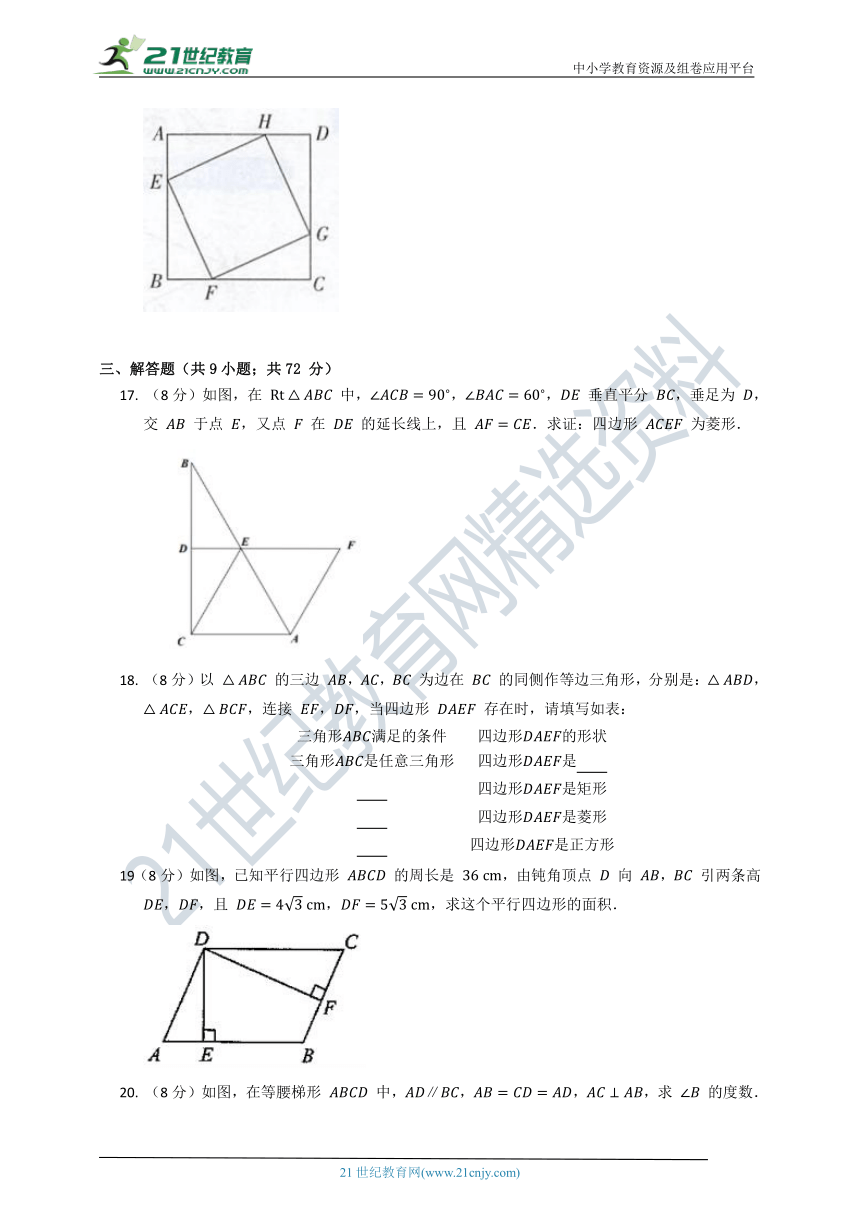
16. 如图所示,正方形 的四个顶点分别在正方形 的四条边上,若正方形 与正方形 的相似比为 ,则 的值为 .
三、解答题(共9小题;共72 分)
17. (8分)如图,在 中,,, 垂直平分 ,垂足为 ,交 于点 ,又点 在 的延长线上,且 .求证:四边形 为菱形.
18. (8分)以 的三边 ,, 为边在 的同侧作等边三角形,分别是:,,,连接 ,,当四边形 存在时,请填写如表:
19(8分)如图,已知平行四边形 的周长是 ,由钝角顶点 向 , 引两条高 ,,且 ,,求这个平行四边形的面积.
20. (8分)如图,在等腰梯形 中,,,,求 的度数.
21. (8分)如图,四边形 是平行四边形, 过 的中点 且交 的延长线于点 .连接 ,.
(1)求证:;
(2)若 且 ,判断四边形 是什么特殊四边形 请说明理由.
22. (8分)如图,在平行四边形 中, 为 的中点,连接 并延长交 的延长线于点 ,连接 ,,若 ,求证:四边形 是矩形.
23.(8分) 如图,已知菱形 的对角线 , 相交于点 ,,.求菱形的高 .
24.(8分) 已知:如图,等腰梯形 中,, 分别是两底 , 的中点,, 分别是 , 的中点.
求证:四边形 是菱形.
25. (8分)如图,在平行四边形 中, 为 的中点,连接 并延长交 的延长线于点 .
(1)求证:;
(2)当 与 满足什么数量关系时,四边形 是矩形,并说明理由.
答案
第一部分
1. A
2. C
3. D
4. C
5. D
【解析】当 时,根据对角线互相垂直的平行四边形是菱形,可以判定平行四边形 是菱形.
6. B
7. D 【解析】做如图辅助线 ,,
由题意得:,
所以 ,
在 中,由勾股定理得:,,,
所以梯形面积:.
8. D
9. D 【解析】,,
四边形 是平行四边形,
四边形 是矩形,
,
四边形 是菱形,
,,
,
,
,
同理:四边形 是矩形,
,
,
第 个平行四边形的面积是:,
.
10. C
第二部分
11. ②③
【解析】通过观察可得应带②③两块碎玻璃.
12. 直角
13.
14. 平行,相等,相等,相等
15. ①②③④
【解析】如图 ,剪成两个等腰直角三角形时可以拼成等腰直角三角形.
如图 ,剪成两个梯形可以拼成对角互补的四边形.
如图 ,图 ,剪成两个全等的梯形可以拼成五边形和六边形.
所以,正确结论的序号是①②③④.
16.
【解析】 正方形 与正方形 的相似比为 ,
不妨假设 ,.
,
,,
.
,
,
.
设 ,则 ,
在 中,
,
,整理得 ,解得 或 (舍),
,,
.
第三部分
17. 关键得出等边 ,等边 .
18. 平行四边形;;;,
19.
.
设 ,则 ,
.
,
,
.
.
20. 提示:设 ,
因为 且 ,可证 ,
而 ,
所以 ,
又 ,
在 中 ,,
所以 .
21. (1) 四边形 是平行四边形,
,
,
是 中点,
,
,,,
.
(2) 四边形 是正方形.
理由如下:
由()易知四边形 是平行四边形,
,
,
,
,,
,
,
,
,
即 ,
四边形 是矩形,
,
四边形 是正方形.
22. 在平行四边形 中,,
,
为 的中点,
,
又 ,
,
,
又 ,
四边形 是平行四边形,
在平行四边形 中,,
又 ,
,
平行四边形 是矩形.
23. 由 , 得菱形边长 ,利用 ,得 .
24. 由三角形中位线定理知 且 , 且 ,
可证 ,得 ,
所以四边形 是菱形.
25. (1) .
(2) , 得平行四边形 ,当 时,平行四边形 为矩形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版2021-2022学年八年级(下)第十八章平行四边形检测试卷C
(时间120分钟,满分120分)
一、选择题(共10小题;每小题3分,共30分)
1. 如图,在四边形 中,,,若 ,则 的度数为
A. B. C. D.
2. 下列说法正确的是
A. 一组对边平行的四边形是梯形
B. 一组对边平行且相等的四边形是梯形
C. 一组对边平行且不相等的四边形是梯形
D. 只有一组对边相等的四边形是梯形
3. 下列结论正确的是
A. 邻角相等的四边形是菱形
B. 有一组邻边相等的四边形是菱形
C. 对角线互相垂直的四边形是菱形
D. 对角线互相垂直平分的四边形是菱形
4. 下列条件不能判定四边形 是平行四边形的是
A. , B. ,
C. , D. ,
5. 下列条件中,能判定平行四边形 是菱形的是
A. B. C. D.
6. 如图,要测定被池塘隔开的 , 两点的距离,可以在 外选一点 ,连接 ,,并分别找出它们的中点 ,,连接 .现测得 ,,,则
A. B. C. D.
7. 已知:梯形的四边分别为 ,,,,则这个梯形的面积是
A. B. C. D.
8. 如图,已知直线 ,小王在直线 上任取 个点:,,,,,经测量发现它们到直线 的距离都是 ;小丁在直线 上任取 个点:,,,,,经测量发现它们到直线 的距离 也都是 .该操作反映了平行线的某种性质,下列对该性质的描述中,不正确的是
A. 如果直线 ,那么直线 上任意一点到直线 的距离都相等
B. 如果直线 ,那么直线 上任意一点到直线 的距离都相等
C. 两条平行线中,任意一条直线上的所有点到另一条直线的距离是一个定值
D. 两条平行线中,一条直线上的任意一点与另一条直线上的任意一点之间的距离都是一个定值
9. 如图所示,在矩形 中,,,两条对角线相交于点 .以 , 为邻边作第 个平行四边形 ,对角线相交于点 ;再以 , 为邻边作第 平行四边形个 ,对角线相交于点 ;再以 , 为邻边作第 个平行四边形 ;,依此类推,第 个平行四边形的面积为
A. B. C. D.
10. 如图,在梯形 中,,连接 , 交于 点,则图中面积相等的三角形共有
A. 对 B. 对 C. 对 D. 对
二、填空题(共6小题;每小题3分,共18分)
11. 小敏不慎将一块平行四边形玻璃打碎成如图所示的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带来了两块碎玻璃,其编号应该是 .
12. 有一个角是 的平行四边形是矩形.
13. 在四边形 中,如果 且 ,,那么 .
14. 请完善本课时知识结构图
15. 将正方形纸片以适当的方式折叠一次,沿折痕剪开后得到两块小纸片,用这两块小纸片拼接成一个新的多边形(不重叠、无缝隙),给出以下结论:
①可以拼成等腰直角三角形;
②可以拼成对角互补的四边形;
③可以拼成五边形;
④可以拼成六边形.
其中所有正确结论的序号是 .
16. 如图所示,正方形 的四个顶点分别在正方形 的四条边上,若正方形 与正方形 的相似比为 ,则 的值为 .
三、解答题(共9小题;共72 分)
17. (8分)如图,在 中,,, 垂直平分 ,垂足为 ,交 于点 ,又点 在 的延长线上,且 .求证:四边形 为菱形.
18. (8分)以 的三边 ,, 为边在 的同侧作等边三角形,分别是:,,,连接 ,,当四边形 存在时,请填写如表:
19(8分)如图,已知平行四边形 的周长是 ,由钝角顶点 向 , 引两条高 ,,且 ,,求这个平行四边形的面积.
20. (8分)如图,在等腰梯形 中,,,,求 的度数.
21. (8分)如图,四边形 是平行四边形, 过 的中点 且交 的延长线于点 .连接 ,.
(1)求证:;
(2)若 且 ,判断四边形 是什么特殊四边形 请说明理由.
22. (8分)如图,在平行四边形 中, 为 的中点,连接 并延长交 的延长线于点 ,连接 ,,若 ,求证:四边形 是矩形.
23.(8分) 如图,已知菱形 的对角线 , 相交于点 ,,.求菱形的高 .
24.(8分) 已知:如图,等腰梯形 中,, 分别是两底 , 的中点,, 分别是 , 的中点.
求证:四边形 是菱形.
25. (8分)如图,在平行四边形 中, 为 的中点,连接 并延长交 的延长线于点 .
(1)求证:;
(2)当 与 满足什么数量关系时,四边形 是矩形,并说明理由.
答案
第一部分
1. A
2. C
3. D
4. C
5. D
【解析】当 时,根据对角线互相垂直的平行四边形是菱形,可以判定平行四边形 是菱形.
6. B
7. D 【解析】做如图辅助线 ,,
由题意得:,
所以 ,
在 中,由勾股定理得:,,,
所以梯形面积:.
8. D
9. D 【解析】,,
四边形 是平行四边形,
四边形 是矩形,
,
四边形 是菱形,
,,
,
,
,
同理:四边形 是矩形,
,
,
第 个平行四边形的面积是:,
.
10. C
第二部分
11. ②③
【解析】通过观察可得应带②③两块碎玻璃.
12. 直角
13.
14. 平行,相等,相等,相等
15. ①②③④
【解析】如图 ,剪成两个等腰直角三角形时可以拼成等腰直角三角形.
如图 ,剪成两个梯形可以拼成对角互补的四边形.
如图 ,图 ,剪成两个全等的梯形可以拼成五边形和六边形.
所以,正确结论的序号是①②③④.
16.
【解析】 正方形 与正方形 的相似比为 ,
不妨假设 ,.
,
,,
.
,
,
.
设 ,则 ,
在 中,
,
,整理得 ,解得 或 (舍),
,,
.
第三部分
17. 关键得出等边 ,等边 .
18. 平行四边形;;;,
19.
.
设 ,则 ,
.
,
,
.
.
20. 提示:设 ,
因为 且 ,可证 ,
而 ,
所以 ,
又 ,
在 中 ,,
所以 .
21. (1) 四边形 是平行四边形,
,
,
是 中点,
,
,,,
.
(2) 四边形 是正方形.
理由如下:
由()易知四边形 是平行四边形,
,
,
,
,,
,
,
,
,
即 ,
四边形 是矩形,
,
四边形 是正方形.
22. 在平行四边形 中,,
,
为 的中点,
,
又 ,
,
,
又 ,
四边形 是平行四边形,
在平行四边形 中,,
又 ,
,
平行四边形 是矩形.
23. 由 , 得菱形边长 ,利用 ,得 .
24. 由三角形中位线定理知 且 , 且 ,
可证 ,得 ,
所以四边形 是菱形.
25. (1) .
(2) , 得平行四边形 ,当 时,平行四边形 为矩形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
