北师大版七年级数学下册 4.2 图形的全等 课件(共40张PPT)
文档属性
| 名称 | 北师大版七年级数学下册 4.2 图形的全等 课件(共40张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 00:00:00 | ||
图片预览








文档简介
(共40张PPT)
4.2 图形的全等
埃舍尔,荷兰科学思维版画大师,20世纪画坛中伟大的艺术家。在1956年举办的艺次画展,得到了众多数学家的赞赏。
埃舍尔的作品以平面镶嵌、不可能的结构、悖论、循环等为特点,数学的原则和思想在他的作品中得到了非同寻常的形象化。
欣赏 埃舍尔 艺术作品
下列各组图形能够完全重合吗?
(1)
(4)
(3)
(2)
(5)
能够完全重合
(1)
(2)
(3)
思考
每组的两个图形大小和形状有什么特点?
观察
大小相同,形状相同,能够完全重合
形状相同,大小也相同。
能够完全重合的两个图形 叫做全等图形
一、全等图形的定义:
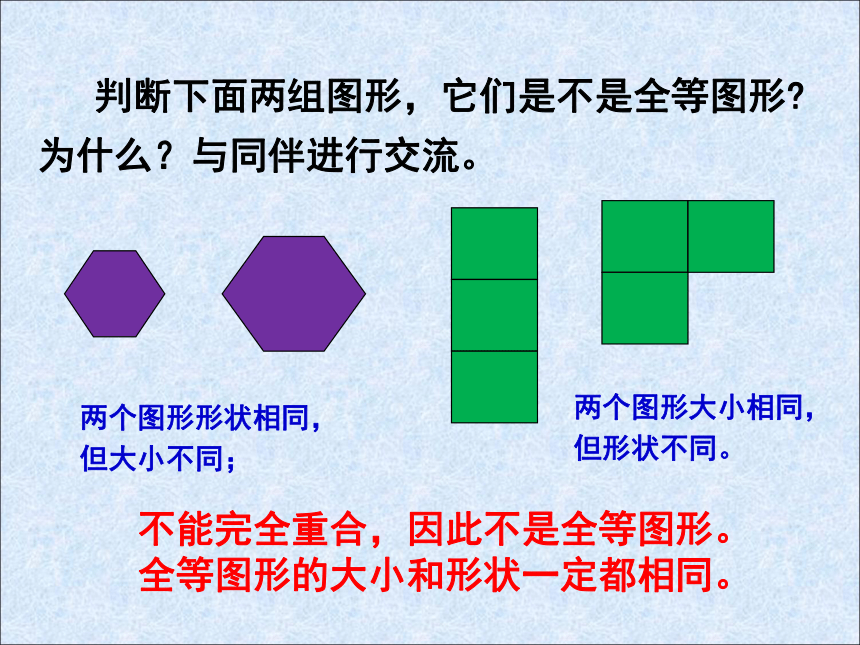
判断下面两组图形,它们是不是全等图形 为什么?与同伴进行交流。
两个图形形状相同,
但大小不同;
两个图形大小相同,
但形状不同。
不能完全重合,因此不是全等图形。全等图形的大小和形状一定都相同。
1、你能列举生活中全等图形的例子吗
议一议
2、 如果两个图形全等,它们的形状大小一定都相同吗?
二、全等图形的性质:
全等图形的形状和大小都相同
形状和大小一定相同
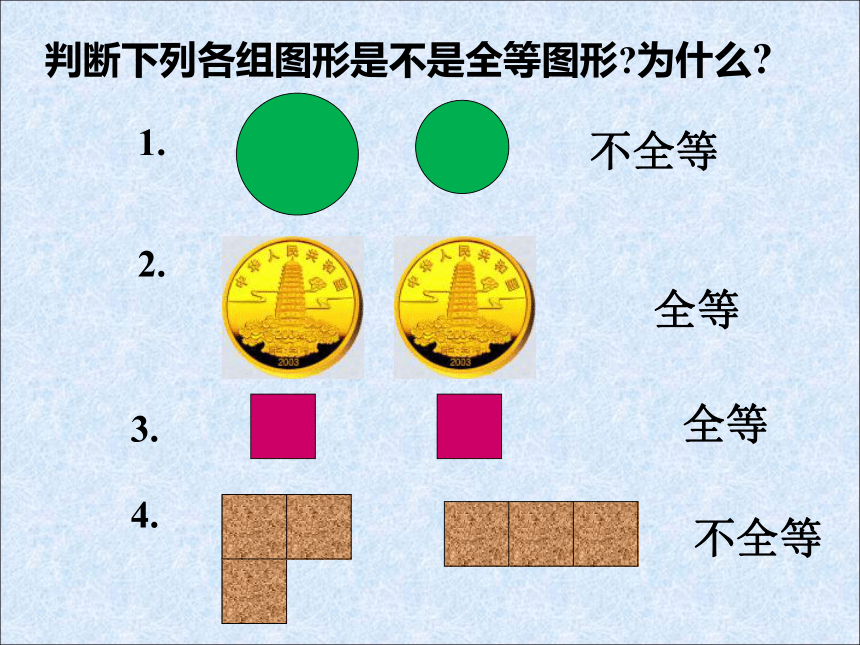
判断下列各组图形是不是全等图形 为什么
1.
2.
3.
4.
不全等
全等
全等
不全等
D
E
F
A
B
C
三、全等三角形的定义:
能够完全重合的两个三角形叫做全等三角形。
能够完全重合的两个图形 叫做全等图形
1、下列两个三角形是怎样由一个三角形得到另一个三角形?它们有什么特点?
B
A
C
N
P
M
A
C
B
D
E
2、下列两个三角形是怎样由一个三角形得到另一个三角形?它们有什么特点?
A
B
C
D
C
B
A
D
E
3、下列两个三角形是怎样由一个三角形得到另一个三角形?它们有什么特点?
B
D
C
一个三角形经过平移、旋转、翻折后所得到的三角形与原三角形全等。
A
B
C
D
E
F
D
C
O
A
B
N
M
S
O
T
你能总结出哪些图形变换可以判定两个三角形全等吗?
平移
旋转
翻折
结论:一个三角形经过平移、翻折、旋转等变换,变换后三角形与原三角形是全等三角形。
A
B
C
D
E
F
其中重合的顶点叫__________
其中重合的边叫_______
其中重合的角叫_______
对应顶点
对应角
对应边
点A、点F的对应顶点分别是___、 ___
AB、DF的对应边分别是___、 ___
∠A、∠F的对应角分别是___、 ___
D
C
DE
AC
∠D
∠C
△ABC与△DEF是全等三角形
四、全等三角形的对应元素:
A
B
C
A1
B1
C1
对应角:∠A ∠A1, ∠B ∠B1, ∠C ∠C1
和
和
和
对应顶点:点A和点A1,点B和点B1,点C和点C1,
和
和
和
对应边:AB A1B1,AC A1C1,BC B1C1
全等三角形的对应元素:
D
E
F
A
B
C
如图:△ABC 与△DEF全等
记作: △ABC ≌ △DEF
读作: △ABC 全等于 △DEF
“全等”符号“≌”,读作“全等于”
注意:两个三角形全等在表示时通常把对应顶点的字母写在对应的位置上。
A
B
C
D
E
F
≌
≌
!
注意
表示两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上。
A
B
C
E
D
F
“全等”用符号“≌ ”表示
图中的△ABC和△DEF全等,
记作:△ABC≌ △DEF
读作:△ABC全等于△DEF
你能否直接从记作 ABC≌ DEF中判断出所有的对应顶点、对应边和对应角?
S
O
T
D
C
N
M
O
A
B
两个全等三角形的位置变化了,对应边、对应角的大小有没有变化?由此你能得到什么结论?
寻找各图中两个全等三角形的对应元素。看谁找的又快有准?
E
A
D
C
B
F
全等三角形的对应边相等,全等三角形的对应角相等.
如图:∵△ABC≌ △DFE
∴ AB=DF, BC=FE, AC=DE
几何语言:
∵△ABC≌ △DFE
∴∠A=∠D,∠B=∠F,∠C=∠E
D
E
F
A
B
C
图形语言:
对应顶点:点A和点A1,点B和点B1,点C和点C1,
对应边:AB = A1B1,AC = A1C1,BC = B1C1
对应角:∠A = ∠A1, ∠B = ∠B1,∠C = ∠C1
A
B
C
A1
B1
C1
全等三角形的性质:对应边相等,对应角相等。
例题讲解,掌握新知
1、如图△ABC≌△DCB,
指出所有的对应边与对应角。
O
D
C
B
A
解:∵△ABC≌△DCB
∴AB与DC,BC与CB,AC与BD是对应边
∠A与∠ D,∠ABC与∠DCB,
∠ACB与∠DBC是对应角
例题讲解,掌握新知
O
D
C
B
A
2、图中△ABO≌△DCO,试写出这两个三角形中相等的边和相等的角。
解:∵△ABO≌△DCO
∴AB=DC,BO=CO,AO=DO
∠A=∠ D,∠ABO=∠DCO,
∠AOB=∠DOC
A
B
C
D
E
F
解:∵△ACB≌△DEF
∴AB=DF, CB=EF,AC=DE.
∴∠A=∠D,∠CBA=∠F,∠C= ∠DEF.
1、先写出全等式,再指 出它们的对应边和对应角。
A
B
C
D
解:∵△ABC≌△ABD
∴AB=AB,BC=BD,AC=AD.
∴∠BAC=∠BAD,∠ABC=∠ABD
∠C= ∠D.
规律一:有公共边的,公共边是对应边
2、先写出全等式,再指出它们的对应边和对应角。
A
C
D
B
解:∵△AOC≌△BOD
∴AO=BO,AC=BD,OC=OD.
∴∠A=∠B,∠C=∠D,
∠AOC= ∠BOD.
规律二:有对顶角的,对顶角是对应角
o
3、 先写出全等式,再指出它们的对应边和对应角。
A
B
C
D
E
解:∵△ABC≌△ADE
∴AB=AD,AC=AE,
BC=DE
∴∠A=∠A,∠B=∠D,
∠ACB= ∠AED.
规律三:有公共角的,公共角是对应角
4、先写出全等式,再指出它们的对应边和对应角。
5、先写出全等式,再指出它们的对应边和对应角。
解:∵△ABC≌△FDE
∴AB=FD,AC=FE,
BC=DE
∴∠A=∠F,∠B=∠D,
∠ACB= ∠FED.
规律五:一对最大的角是对应角
一对最小的角是对应角
A
B
C
F
D
E
规律四:一对最长的边是对应边
一对最短的边是对应边
1、全等用符号 表示,读作: 。
2、判断题
(1)全等三角形的对应边相等,对应角相等( )
(2)全等三角形的周长相等,面积也相等。 ( )
(3)面积相等的三角形是全等三角形。 ( )
(4)周长相等的三角形是全等三角形。 ( )
随堂检测
≌
全等于
√
√
X
X
3、如图△ABC≌△ADE, ∠C=∠E, BC=DE,
对应边:_____________
对应角:_____________
A
B
C
D
E
A
B
C
D
4、如图,紫色三角形经过翻折得到蓝色三角形,写出图中的全等三角形:_________ ;
对应边有 :_____________;
对应角有:_____________。
下图是一个等边三角形,你能把它分成两个全等三角形吗?你能把它分成三个全等三角形吗?四个呢?试试看?
互相重合的顶点叫做 。
互相重合的角叫做 。
互相重合的边叫做 。
其中
2.___________________________叫做全等三角形。
1.能够重合的两个图形叫做 。
全等图形
4.全等图形的 和 相等
对应边
对应角
对应顶点
能够完全重合的两个三角形
3.“全等”用符号“ ”来表示,读作“ ”
对应边
对应角
5.书写全等式时要求把对应字母放在对应 的位置上
全等于
≌
课堂小结
6、全等三角形找对应边、对应角的规律与方法:
(1)有公共边的,公共边一定是对应边,
有对顶角或公共角的,对顶角或公共角一定是对应角;
(2)对应角所对的边是对应边,对应边所对的角是对应角;
(3)最大边与最大边(最小边与最小边)为对应边;
最大角与最大角(最小角与最小角)为对应角;
课堂小结
。
作业布置
1、学练优P60,
2、思考题:沿着右边图中的虚线,分别把右面的图形 划分为两个全等图形,并与同 伴进行交流。
图形划分方法如下:你们学会了吗?
谢谢各位!
4.2 图形的全等
埃舍尔,荷兰科学思维版画大师,20世纪画坛中伟大的艺术家。在1956年举办的艺次画展,得到了众多数学家的赞赏。
埃舍尔的作品以平面镶嵌、不可能的结构、悖论、循环等为特点,数学的原则和思想在他的作品中得到了非同寻常的形象化。
欣赏 埃舍尔 艺术作品
下列各组图形能够完全重合吗?
(1)
(4)
(3)
(2)
(5)
能够完全重合
(1)
(2)
(3)
思考
每组的两个图形大小和形状有什么特点?
观察
大小相同,形状相同,能够完全重合
形状相同,大小也相同。
能够完全重合的两个图形 叫做全等图形
一、全等图形的定义:
判断下面两组图形,它们是不是全等图形 为什么?与同伴进行交流。
两个图形形状相同,
但大小不同;
两个图形大小相同,
但形状不同。
不能完全重合,因此不是全等图形。全等图形的大小和形状一定都相同。
1、你能列举生活中全等图形的例子吗
议一议
2、 如果两个图形全等,它们的形状大小一定都相同吗?
二、全等图形的性质:
全等图形的形状和大小都相同
形状和大小一定相同
判断下列各组图形是不是全等图形 为什么
1.
2.
3.
4.
不全等
全等
全等
不全等
D
E
F
A
B
C
三、全等三角形的定义:
能够完全重合的两个三角形叫做全等三角形。
能够完全重合的两个图形 叫做全等图形
1、下列两个三角形是怎样由一个三角形得到另一个三角形?它们有什么特点?
B
A
C
N
P
M
A
C
B
D
E
2、下列两个三角形是怎样由一个三角形得到另一个三角形?它们有什么特点?
A
B
C
D
C
B
A
D
E
3、下列两个三角形是怎样由一个三角形得到另一个三角形?它们有什么特点?
B
D
C
一个三角形经过平移、旋转、翻折后所得到的三角形与原三角形全等。
A
B
C
D
E
F
D
C
O
A
B
N
M
S
O
T
你能总结出哪些图形变换可以判定两个三角形全等吗?
平移
旋转
翻折
结论:一个三角形经过平移、翻折、旋转等变换,变换后三角形与原三角形是全等三角形。
A
B
C
D
E
F
其中重合的顶点叫__________
其中重合的边叫_______
其中重合的角叫_______
对应顶点
对应角
对应边
点A、点F的对应顶点分别是___、 ___
AB、DF的对应边分别是___、 ___
∠A、∠F的对应角分别是___、 ___
D
C
DE
AC
∠D
∠C
△ABC与△DEF是全等三角形
四、全等三角形的对应元素:
A
B
C
A1
B1
C1
对应角:∠A ∠A1, ∠B ∠B1, ∠C ∠C1
和
和
和
对应顶点:点A和点A1,点B和点B1,点C和点C1,
和
和
和
对应边:AB A1B1,AC A1C1,BC B1C1
全等三角形的对应元素:
D
E
F
A
B
C
如图:△ABC 与△DEF全等
记作: △ABC ≌ △DEF
读作: △ABC 全等于 △DEF
“全等”符号“≌”,读作“全等于”
注意:两个三角形全等在表示时通常把对应顶点的字母写在对应的位置上。
A
B
C
D
E
F
≌
≌
!
注意
表示两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上。
A
B
C
E
D
F
“全等”用符号“≌ ”表示
图中的△ABC和△DEF全等,
记作:△ABC≌ △DEF
读作:△ABC全等于△DEF
你能否直接从记作 ABC≌ DEF中判断出所有的对应顶点、对应边和对应角?
S
O
T
D
C
N
M
O
A
B
两个全等三角形的位置变化了,对应边、对应角的大小有没有变化?由此你能得到什么结论?
寻找各图中两个全等三角形的对应元素。看谁找的又快有准?
E
A
D
C
B
F
全等三角形的对应边相等,全等三角形的对应角相等.
如图:∵△ABC≌ △DFE
∴ AB=DF, BC=FE, AC=DE
几何语言:
∵△ABC≌ △DFE
∴∠A=∠D,∠B=∠F,∠C=∠E
D
E
F
A
B
C
图形语言:
对应顶点:点A和点A1,点B和点B1,点C和点C1,
对应边:AB = A1B1,AC = A1C1,BC = B1C1
对应角:∠A = ∠A1, ∠B = ∠B1,∠C = ∠C1
A
B
C
A1
B1
C1
全等三角形的性质:对应边相等,对应角相等。
例题讲解,掌握新知
1、如图△ABC≌△DCB,
指出所有的对应边与对应角。
O
D
C
B
A
解:∵△ABC≌△DCB
∴AB与DC,BC与CB,AC与BD是对应边
∠A与∠ D,∠ABC与∠DCB,
∠ACB与∠DBC是对应角
例题讲解,掌握新知
O
D
C
B
A
2、图中△ABO≌△DCO,试写出这两个三角形中相等的边和相等的角。
解:∵△ABO≌△DCO
∴AB=DC,BO=CO,AO=DO
∠A=∠ D,∠ABO=∠DCO,
∠AOB=∠DOC
A
B
C
D
E
F
解:∵△ACB≌△DEF
∴AB=DF, CB=EF,AC=DE.
∴∠A=∠D,∠CBA=∠F,∠C= ∠DEF.
1、先写出全等式,再指 出它们的对应边和对应角。
A
B
C
D
解:∵△ABC≌△ABD
∴AB=AB,BC=BD,AC=AD.
∴∠BAC=∠BAD,∠ABC=∠ABD
∠C= ∠D.
规律一:有公共边的,公共边是对应边
2、先写出全等式,再指出它们的对应边和对应角。
A
C
D
B
解:∵△AOC≌△BOD
∴AO=BO,AC=BD,OC=OD.
∴∠A=∠B,∠C=∠D,
∠AOC= ∠BOD.
规律二:有对顶角的,对顶角是对应角
o
3、 先写出全等式,再指出它们的对应边和对应角。
A
B
C
D
E
解:∵△ABC≌△ADE
∴AB=AD,AC=AE,
BC=DE
∴∠A=∠A,∠B=∠D,
∠ACB= ∠AED.
规律三:有公共角的,公共角是对应角
4、先写出全等式,再指出它们的对应边和对应角。
5、先写出全等式,再指出它们的对应边和对应角。
解:∵△ABC≌△FDE
∴AB=FD,AC=FE,
BC=DE
∴∠A=∠F,∠B=∠D,
∠ACB= ∠FED.
规律五:一对最大的角是对应角
一对最小的角是对应角
A
B
C
F
D
E
规律四:一对最长的边是对应边
一对最短的边是对应边
1、全等用符号 表示,读作: 。
2、判断题
(1)全等三角形的对应边相等,对应角相等( )
(2)全等三角形的周长相等,面积也相等。 ( )
(3)面积相等的三角形是全等三角形。 ( )
(4)周长相等的三角形是全等三角形。 ( )
随堂检测
≌
全等于
√
√
X
X
3、如图△ABC≌△ADE, ∠C=∠E, BC=DE,
对应边:_____________
对应角:_____________
A
B
C
D
E
A
B
C
D
4、如图,紫色三角形经过翻折得到蓝色三角形,写出图中的全等三角形:_________ ;
对应边有 :_____________;
对应角有:_____________。
下图是一个等边三角形,你能把它分成两个全等三角形吗?你能把它分成三个全等三角形吗?四个呢?试试看?
互相重合的顶点叫做 。
互相重合的角叫做 。
互相重合的边叫做 。
其中
2.___________________________叫做全等三角形。
1.能够重合的两个图形叫做 。
全等图形
4.全等图形的 和 相等
对应边
对应角
对应顶点
能够完全重合的两个三角形
3.“全等”用符号“ ”来表示,读作“ ”
对应边
对应角
5.书写全等式时要求把对应字母放在对应 的位置上
全等于
≌
课堂小结
6、全等三角形找对应边、对应角的规律与方法:
(1)有公共边的,公共边一定是对应边,
有对顶角或公共角的,对顶角或公共角一定是对应角;
(2)对应角所对的边是对应边,对应边所对的角是对应角;
(3)最大边与最大边(最小边与最小边)为对应边;
最大角与最大角(最小角与最小角)为对应角;
课堂小结
。
作业布置
1、学练优P60,
2、思考题:沿着右边图中的虚线,分别把右面的图形 划分为两个全等图形,并与同 伴进行交流。
图形划分方法如下:你们学会了吗?
谢谢各位!
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
