青岛版八年级数学上册 4.5 方差(1)课件(共18张PPT)
文档属性
| 名称 | 青岛版八年级数学上册 4.5 方差(1)课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
4.5 方差(1)
01
学习目标
05
随堂练习
06
课堂小结
03
新知探究
02
情境引入
04
例题精讲
1.了解离差和方差的定义和计算公式。
2.理解方差概念的产生和形成的过程。
3.会用方差计算公式来比较两组数据的波动大小。
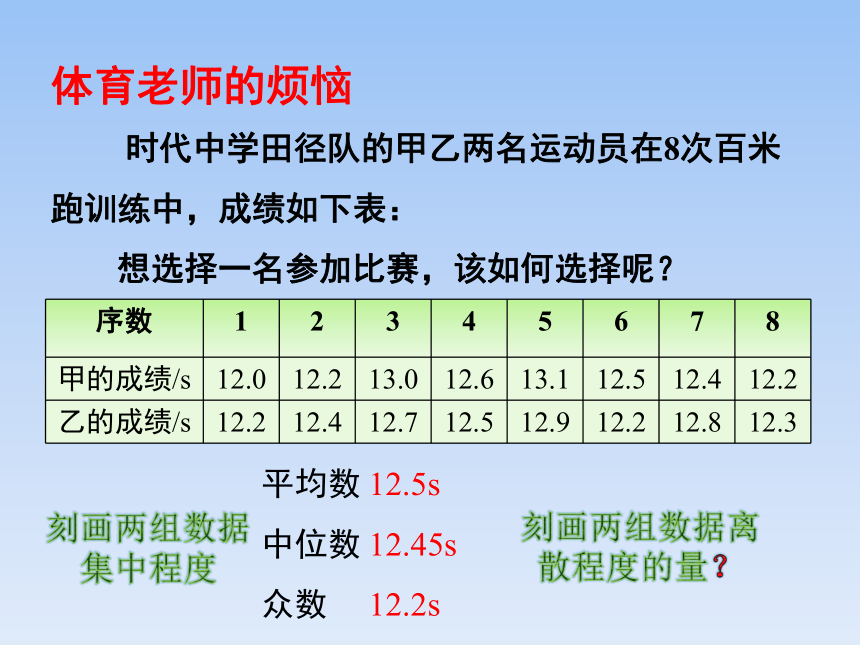
时代中学田径队的甲乙两名运动员在8次百米跑训练中,成绩如下表:
想选择一名参加比赛,该如何选择呢?
序数 1 2 3 4 5 6 7 8
甲的成绩/s 12.0 12.2 13.0 12.6 13.1 12.5 12.4 12.2
乙的成绩/s 12.2 12.4 12.7 12.5 12.9 12.2 12.8 12.3
平均数
中位数
众数
12.2s
12.45s
12.5s
序数 1 2 3 4 5 6 7 8
甲 -0.5 -0.3 0.5 0.1 0.6 0 -0.1 -0.3
乙 -0.3 -0.1 0.2 0 0.4 -0.3 0.3 -0.2
甲的第一次测试成绩与平均成绩的差是-0.5,说明他这次的成绩比平均成绩快0.5秒。
为了刻画一组数据的离散程度,通常选用_______________________________来刻画这组数据的离散程度.
即
我们把它叫做这组数据的方差.
1.甲、乙两个运动员8次百米跑成绩的波动情况是( )
A.甲的波动比乙大 B.乙的波动比甲大
C.甲、乙波动一样大 D.无法比较
2.有5名同学目测同一本教科书的宽度时,产生的误差如下(单位:cm):2,-2,-1,1,0。则这组数据的方差为______.
练习
A
2 cm
方差越大,说明数据的波动越大,越不稳定.
方差用来衡量一组数据的波动大小.(即这组数据偏离平均数的大小).
计算方差的步骤可概括为
“先平均,后求差,平方后,再平均”.
例:为了考察甲、乙两种小麦的长势,分别从中抽出10株苗,测得苗高如下(单位:cm):
甲: 12 13 14 15 10 16 13 11 15 11
乙: 11 16 17 14 13 19 6 8 10 16
问哪种小麦长得比较整齐
思考:求数据方差的一般步骤是什么?
1.求数据的平均数;
2.利用方差公式求方差。
解:1)计算甲的平均数和方差:
2)计算乙的平均数和方差:
所以,甲小麦长的比较整齐.
1.(1)已知数据1,4,3, 5,2,则这5个数的方差是____.
(2)绝对值小于 的所有整数的方差是______.
(3)一组数据:a, a, a, …,a (有n个a),则它的方差为___;
2.在一次芭蕾舞的比赛中,甲,乙两个芭蕾舞团表演了舞剧<<天鹅舞>>,参加表演的女演员的身高(单位:cm)分别是:
甲团 163 164 164 165 165 165 166 167
乙团 163 164 164 165 166 167 167 168
哪个芭蕾舞女演员的身高更整齐
方差用来衡量一组数据的波动大小(即这组数据偏离平均数的大小).方差越大,说明数据的波动越大,越不稳定.
2.方差:各数据与它们的平均数的差的平方的平均数.
作业:
课本第138页练习第1,2题
4.5 方差(1)
01
学习目标
05
随堂练习
06
课堂小结
03
新知探究
02
情境引入
04
例题精讲
1.了解离差和方差的定义和计算公式。
2.理解方差概念的产生和形成的过程。
3.会用方差计算公式来比较两组数据的波动大小。
时代中学田径队的甲乙两名运动员在8次百米跑训练中,成绩如下表:
想选择一名参加比赛,该如何选择呢?
序数 1 2 3 4 5 6 7 8
甲的成绩/s 12.0 12.2 13.0 12.6 13.1 12.5 12.4 12.2
乙的成绩/s 12.2 12.4 12.7 12.5 12.9 12.2 12.8 12.3
平均数
中位数
众数
12.2s
12.45s
12.5s
序数 1 2 3 4 5 6 7 8
甲 -0.5 -0.3 0.5 0.1 0.6 0 -0.1 -0.3
乙 -0.3 -0.1 0.2 0 0.4 -0.3 0.3 -0.2
甲的第一次测试成绩与平均成绩的差是-0.5,说明他这次的成绩比平均成绩快0.5秒。
为了刻画一组数据的离散程度,通常选用_______________________________来刻画这组数据的离散程度.
即
我们把它叫做这组数据的方差.
1.甲、乙两个运动员8次百米跑成绩的波动情况是( )
A.甲的波动比乙大 B.乙的波动比甲大
C.甲、乙波动一样大 D.无法比较
2.有5名同学目测同一本教科书的宽度时,产生的误差如下(单位:cm):2,-2,-1,1,0。则这组数据的方差为______.
练习
A
2 cm
方差越大,说明数据的波动越大,越不稳定.
方差用来衡量一组数据的波动大小.(即这组数据偏离平均数的大小).
计算方差的步骤可概括为
“先平均,后求差,平方后,再平均”.
例:为了考察甲、乙两种小麦的长势,分别从中抽出10株苗,测得苗高如下(单位:cm):
甲: 12 13 14 15 10 16 13 11 15 11
乙: 11 16 17 14 13 19 6 8 10 16
问哪种小麦长得比较整齐
思考:求数据方差的一般步骤是什么?
1.求数据的平均数;
2.利用方差公式求方差。
解:1)计算甲的平均数和方差:
2)计算乙的平均数和方差:
所以,甲小麦长的比较整齐.
1.(1)已知数据1,4,3, 5,2,则这5个数的方差是____.
(2)绝对值小于 的所有整数的方差是______.
(3)一组数据:a, a, a, …,a (有n个a),则它的方差为___;
2.在一次芭蕾舞的比赛中,甲,乙两个芭蕾舞团表演了舞剧<<天鹅舞>>,参加表演的女演员的身高(单位:cm)分别是:
甲团 163 164 164 165 165 165 166 167
乙团 163 164 164 165 166 167 167 168
哪个芭蕾舞女演员的身高更整齐
方差用来衡量一组数据的波动大小(即这组数据偏离平均数的大小).方差越大,说明数据的波动越大,越不稳定.
2.方差:各数据与它们的平均数的差的平方的平均数.
作业:
课本第138页练习第1,2题
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
