青岛版八年级数学上册 4.3众数 教学课件(共24张PPT)
文档属性
| 名称 | 青岛版八年级数学上册 4.3众数 教学课件(共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 00:00:00 | ||
图片预览





文档简介
(共24张PPT)
4.3 众数
01
学习目标
05
随堂练习
06
课堂小结
03
新知探究
02
旧知回顾
04
例题精讲
1.理解众数的概念,会求一组数据的众数。
2.体会众数、中位数、平均数的区别。
3.能结合具体情境选择众数、中位数、或平均数作为一组数据的代表,用以解释数据的集中程度。
数 据 分 析
平均数
中位数
概念
计算方法
概念
计算方法
方差
众数
应用
应用
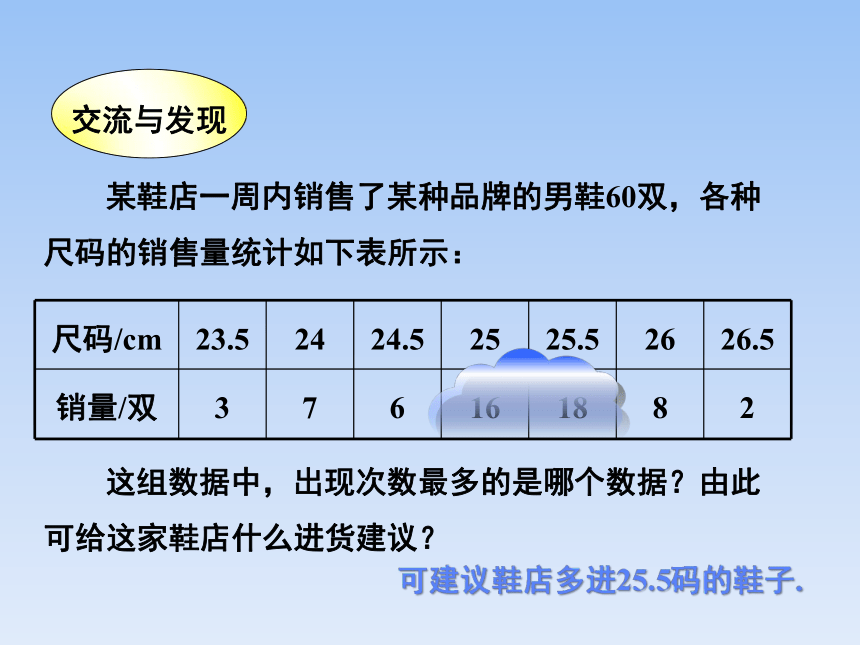
尺码/cm 23.5 24 24.5 25 25.5 26 26.5
销量/双 3 7 6 16 18 8 2
某鞋店一周内销售了某种品牌的男鞋60双,各种尺码的销售量统计如下表所示:
交流与发现
这组数据中,出现次数最多的是哪个数据?由此可给这家鞋店什么进货建议?
可建议鞋店多进25.5码的鞋子.
一组数据中___________ 的数据,叫做这组数据的众数。
出现次数最多
1.数据1,2,3,4,3,5的众数是( )
2.数据1,2,3,4,5,2,1的众数是( )
3
2,1
不存在
3.数据1,2,3,4,5,6的众数是( )
在找各组数据的众数过程中,你发现了什么?
众数与它重复出现的次数有关。
众数必须是这组数据中的一个,而不是相应的次数.
众数具有不唯一性,一组数据可能有一个众数,也可能有多个众数,也可能没有。
众数反应一组数据的多数水平。
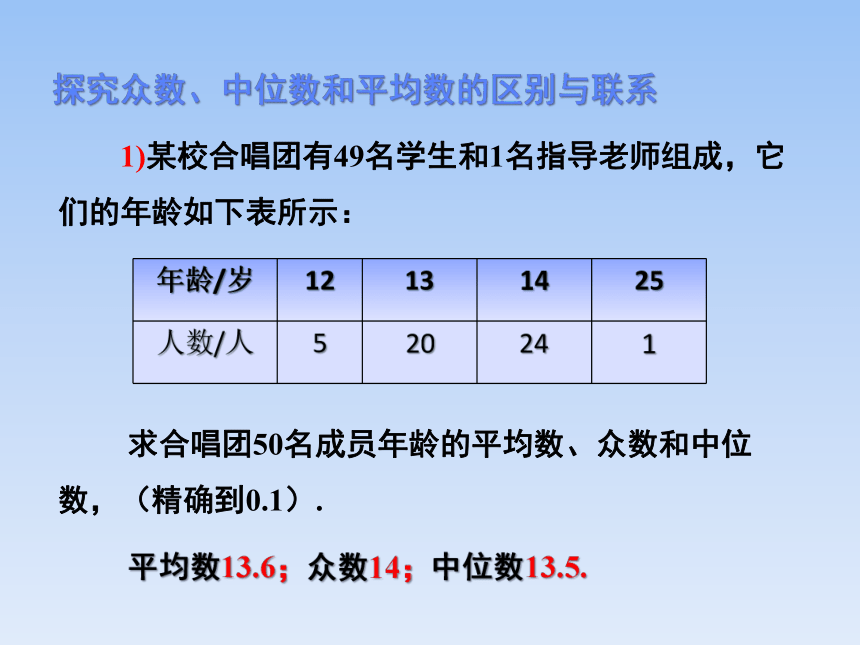
1)某校合唱团有49名学生和1名指导老师组成,它们的年龄如下表所示:
求合唱团50名成员年龄的平均数、众数和中位数,(精确到0.1).
探究众数、中位数和平均数的区别与联系
年龄/岁 12 13 14 25
人数/人 5 20 24 1
平均数13.6;众数14;中位数13.5.
2)如果25岁的教师因为工作需要调离合唱团,换了一位45岁的教师,那么该合唱团成员年龄的平均数,中位数和众数有什么改变?
探究众数、中位数和平均数的区别与联系
平均数14.0;众数14;中位数13.5.
个别极端数字的改变会改变平均数的大小,但对众数和中位数没有影响.
平均数:
中位数:
众 数:
数据代表
通过计算得到,能充分利用所有数据,
但容易受极端数据的影响
只与其在数据中的位置有关,
不能充分利用所有数据
只与其在数据中的重复次数有关,
不能充分利用所有数据
(应用最广)
(集中程度)
平均数反映一组数据的( )
中位数反映一组数据的( )
众数反映一组数据的( )
A.平均水平 B.中等水平 C.多数水平
平均数、中位数和众数分别反映什么?
A
B
C
例1 某公司15名工作人员,他们的月工资情况如下表所示:
职务 经理 副经理 职员
人数 1 2 12
月工资/元 8000 5000 2000
(1)求该公司工作人员月工资的平均数、中位数和众数;
(2)假设经理的月工资由8000元提升到12000,副经理的月工资由5000元提升到6000元,职员的月工资仍为2000元,求工资变动后所得一组新数据的平均数、中位数和众数;
(3)由(1)(2)你认为在这一问题中,哪个统计量更能反映出这个公司员工的月工资水平?结合统计量的实际意义加以解释。
解
(1)该公司工作人员月工资的平均数为
所以,月平均工资为2800元,众数和中位数都是2000元.
(2)改动后月工资的众数和中位数还是2000元,平均数是:
(3)由于经理和副经理的工资偏高,使该公司的原月平均工资2800元与绝大多数员工的工资差距较大。该公司经理和副经理的工资变动后,月平均工资由2800元升至3200元,但中位数和众数仍是2000元。由此可见,在这一问题中,要反映该公司工作人员月工资的水平,用中位数和众数要比平均数更客观一些。
例2 青年歌手大奖赛的决赛在甲乙两名歌手之间进行,9位评委的评分(10分为满分)情况如下表所示(单位:分)
评委编号 1 2 3 4 5 6 7 8 9
甲的得分 8.8 9.5 8.6 9.6 7.2 8.9 8.8 8.8 8.8
乙的得分 8.5 9.1 8.5 9.1 9.9 8.5 9.2 8.6 8.3
(1)将甲、乙两名歌手的得分适当进行分组整理,并列成统计表。
(2)分别求出甲乙两名歌手得分的平均数、中位数和众数。
(3)由(2)的结果,分析甲乙两名歌手中谁的演唱水平较高。
(4)如果以平均分为标准区分比赛的名次,那么制定怎样的计分规则比较合理?
9.6 9.5 8.9 8.8 8.6 7.2
9.9 9.2 9.1 8.6 8.5 8.3
解 (1)分组
1
甲得分情况
乙得分情况
1
1
1
1
4
1
1
3
1
2
1
(2)
甲的中位数是8.8分,众数是8.8分.
乙的中位数是8.6分,众数是8.5分.
(3)从平均分来看,乙的水平较高.
从中位数来看,甲的水平较高。
从众数来看,甲也比乙高,有四位评委给甲8.8分,三位评委给乙8.5分,甲相对较高。
(4)有(1)中统计结果可以看出,乙的平均分略高与甲,原因是个别评委给了极端分,使得出现个别差异较大的数据.因此,若制订“去掉一个最高分和一个最低分”的计分规则,以确保平分的合理性。
按照这个规则,甲、乙的平均分分别是8.89分与8.79分,所以甲的演唱水平较高。
1、在平均数、中位数、众数中,下列情况下用哪一个统计量比较合适。
1)期末考试后各班级排名。
2)面包店店主最关心哪种面包销量好。
3)遇到开奖问题应该关心中奖金额的哪种数据信息。
4)上课间操时,体育老师以哪一行为基准进行整队。
5)裁判一般把什么作为选手的最终得分。
6)选举中,人们通常最关心的数据。
2、判断
1)一组数据的平均数一定只有一个( )
2)一组数据的中位数一定只有一个( )
3)一组数据的众数一定只有一个 ( )
4) 一组数据的众数是这组数据中出现次数最多的数据的次数 ( )
5)一组数据的平均数、中位数、众数可以是同一个数 ( )
3、小明和小亮是同桌,同时也是学习上的竞争对手,进入中学后的七次数学考试的成绩如下:
小明:88, 70, 88, 92, 94, 93, 95
小亮:65, 85, 86, 93, 93, 93, 94
小明和小亮都认为自己的成绩比对方好,你知道为什么吗?你是怎么认为的?
分析:小明的平均分是88.6分,小亮的平均分是87分,小明的中位数是92分,小亮的中位数是93分,但是小明的众数是88分,小亮的众数是93分,且小亮的成绩在不断增加,小明的成绩有波动。
1.众数的概念和意义.
2.众数与平均数,中位数的区别与联系.
4.3 众数
01
学习目标
05
随堂练习
06
课堂小结
03
新知探究
02
旧知回顾
04
例题精讲
1.理解众数的概念,会求一组数据的众数。
2.体会众数、中位数、平均数的区别。
3.能结合具体情境选择众数、中位数、或平均数作为一组数据的代表,用以解释数据的集中程度。
数 据 分 析
平均数
中位数
概念
计算方法
概念
计算方法
方差
众数
应用
应用
尺码/cm 23.5 24 24.5 25 25.5 26 26.5
销量/双 3 7 6 16 18 8 2
某鞋店一周内销售了某种品牌的男鞋60双,各种尺码的销售量统计如下表所示:
交流与发现
这组数据中,出现次数最多的是哪个数据?由此可给这家鞋店什么进货建议?
可建议鞋店多进25.5码的鞋子.
一组数据中___________ 的数据,叫做这组数据的众数。
出现次数最多
1.数据1,2,3,4,3,5的众数是( )
2.数据1,2,3,4,5,2,1的众数是( )
3
2,1
不存在
3.数据1,2,3,4,5,6的众数是( )
在找各组数据的众数过程中,你发现了什么?
众数与它重复出现的次数有关。
众数必须是这组数据中的一个,而不是相应的次数.
众数具有不唯一性,一组数据可能有一个众数,也可能有多个众数,也可能没有。
众数反应一组数据的多数水平。
1)某校合唱团有49名学生和1名指导老师组成,它们的年龄如下表所示:
求合唱团50名成员年龄的平均数、众数和中位数,(精确到0.1).
探究众数、中位数和平均数的区别与联系
年龄/岁 12 13 14 25
人数/人 5 20 24 1
平均数13.6;众数14;中位数13.5.
2)如果25岁的教师因为工作需要调离合唱团,换了一位45岁的教师,那么该合唱团成员年龄的平均数,中位数和众数有什么改变?
探究众数、中位数和平均数的区别与联系
平均数14.0;众数14;中位数13.5.
个别极端数字的改变会改变平均数的大小,但对众数和中位数没有影响.
平均数:
中位数:
众 数:
数据代表
通过计算得到,能充分利用所有数据,
但容易受极端数据的影响
只与其在数据中的位置有关,
不能充分利用所有数据
只与其在数据中的重复次数有关,
不能充分利用所有数据
(应用最广)
(集中程度)
平均数反映一组数据的( )
中位数反映一组数据的( )
众数反映一组数据的( )
A.平均水平 B.中等水平 C.多数水平
平均数、中位数和众数分别反映什么?
A
B
C
例1 某公司15名工作人员,他们的月工资情况如下表所示:
职务 经理 副经理 职员
人数 1 2 12
月工资/元 8000 5000 2000
(1)求该公司工作人员月工资的平均数、中位数和众数;
(2)假设经理的月工资由8000元提升到12000,副经理的月工资由5000元提升到6000元,职员的月工资仍为2000元,求工资变动后所得一组新数据的平均数、中位数和众数;
(3)由(1)(2)你认为在这一问题中,哪个统计量更能反映出这个公司员工的月工资水平?结合统计量的实际意义加以解释。
解
(1)该公司工作人员月工资的平均数为
所以,月平均工资为2800元,众数和中位数都是2000元.
(2)改动后月工资的众数和中位数还是2000元,平均数是:
(3)由于经理和副经理的工资偏高,使该公司的原月平均工资2800元与绝大多数员工的工资差距较大。该公司经理和副经理的工资变动后,月平均工资由2800元升至3200元,但中位数和众数仍是2000元。由此可见,在这一问题中,要反映该公司工作人员月工资的水平,用中位数和众数要比平均数更客观一些。
例2 青年歌手大奖赛的决赛在甲乙两名歌手之间进行,9位评委的评分(10分为满分)情况如下表所示(单位:分)
评委编号 1 2 3 4 5 6 7 8 9
甲的得分 8.8 9.5 8.6 9.6 7.2 8.9 8.8 8.8 8.8
乙的得分 8.5 9.1 8.5 9.1 9.9 8.5 9.2 8.6 8.3
(1)将甲、乙两名歌手的得分适当进行分组整理,并列成统计表。
(2)分别求出甲乙两名歌手得分的平均数、中位数和众数。
(3)由(2)的结果,分析甲乙两名歌手中谁的演唱水平较高。
(4)如果以平均分为标准区分比赛的名次,那么制定怎样的计分规则比较合理?
9.6 9.5 8.9 8.8 8.6 7.2
9.9 9.2 9.1 8.6 8.5 8.3
解 (1)分组
1
甲得分情况
乙得分情况
1
1
1
1
4
1
1
3
1
2
1
(2)
甲的中位数是8.8分,众数是8.8分.
乙的中位数是8.6分,众数是8.5分.
(3)从平均分来看,乙的水平较高.
从中位数来看,甲的水平较高。
从众数来看,甲也比乙高,有四位评委给甲8.8分,三位评委给乙8.5分,甲相对较高。
(4)有(1)中统计结果可以看出,乙的平均分略高与甲,原因是个别评委给了极端分,使得出现个别差异较大的数据.因此,若制订“去掉一个最高分和一个最低分”的计分规则,以确保平分的合理性。
按照这个规则,甲、乙的平均分分别是8.89分与8.79分,所以甲的演唱水平较高。
1、在平均数、中位数、众数中,下列情况下用哪一个统计量比较合适。
1)期末考试后各班级排名。
2)面包店店主最关心哪种面包销量好。
3)遇到开奖问题应该关心中奖金额的哪种数据信息。
4)上课间操时,体育老师以哪一行为基准进行整队。
5)裁判一般把什么作为选手的最终得分。
6)选举中,人们通常最关心的数据。
2、判断
1)一组数据的平均数一定只有一个( )
2)一组数据的中位数一定只有一个( )
3)一组数据的众数一定只有一个 ( )
4) 一组数据的众数是这组数据中出现次数最多的数据的次数 ( )
5)一组数据的平均数、中位数、众数可以是同一个数 ( )
3、小明和小亮是同桌,同时也是学习上的竞争对手,进入中学后的七次数学考试的成绩如下:
小明:88, 70, 88, 92, 94, 93, 95
小亮:65, 85, 86, 93, 93, 93, 94
小明和小亮都认为自己的成绩比对方好,你知道为什么吗?你是怎么认为的?
分析:小明的平均分是88.6分,小亮的平均分是87分,小明的中位数是92分,小亮的中位数是93分,但是小明的众数是88分,小亮的众数是93分,且小亮的成绩在不断增加,小明的成绩有波动。
1.众数的概念和意义.
2.众数与平均数,中位数的区别与联系.
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
