2021-2022学年苏科版七年级数学下册9.2 单项式乘多项式 同步训练 (word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版七年级数学下册9.2 单项式乘多项式 同步训练 (word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 95.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 09:28:11 | ||
图片预览


文档简介
9.2 单项式乘多项式 同步训练
一、单选题
1.计算 的结果为( )
A. B. C. D
2、计算(-8x2)·(5x3-3x2+x)的结果正确的是( )
A.-40x5-24x4-8x3 B.-40x5+24x4-8x3
C.-40x5+24x4+8x3 D.-40x5-24x4+8x3
3、若□×xy=3x2y+2xy,则□内应填的式子是( )
A.3x+2 B.x+2 C.3xy+2 D.xy+2
4、若2x与一个多项式的积为2x3﹣x2+2x,则这个多项式为( )
A.x2﹣2x+1 B.4x2﹣2x+4 C.x2﹣x+1 D.x2﹣x
5.要使(x2+ax+1)(﹣6x3)的展开式中不含x4项,则a应等于( )
A.6 B.﹣1 C. D.0
6.若整式A与单项式﹣a2b的乘积为a(ab3﹣a3b),则整式A为( )
A. a2﹣b2 B. b2﹣a2 C. a2+b2 D. ﹣a2﹣b2
7.今天数学课上,老师讲了单项式乘以多项式,放学后,小华回到家拿出课堂笔记,认真复习老师课上讲的内容,他突然发现一道题;﹣3xy (4y﹣2x﹣1)=﹣12xy2+6x2y+__________,空格的地方被钢笔水弄污了,你认为横线上应填写( )
A. 3xy B. ﹣3xy C. ﹣1 D. 1
8、若要使x(x2+a)+3x﹣2b=x3+5x+4恒成立,则a,b的值分别是( )
A.﹣2,﹣2 B.2,2 C.2,﹣2 D.﹣2,2
9.要使(x3+ax2-x)·(-8x4)的运算结果中不含x6的项,则a的值应为( )
A.8 B.-8 C. D.0
10.如图,边长为 (m + 3)的正方形纸片剪去一个边 长为 m 的正方形之后,余下部分又剪拼成一个长方形(不重叠无缝隙),若拼成的长方形一边长为 3,则此长方形的周长是( )
A.2m + 6 B.4m + 6 C.4m + 12 D.2m + 12
二、填空题
11.计算:(﹣3xy2)2(2x﹣y2)=________.
12.当a=﹣2时,求a2(2a+1)=________.
13.若﹣2x2y(﹣xmy+3xy3)=2x5y2﹣6x3yn , 则m=________,n=________.
14.A、B为单项式,且5x(A﹣2y)=30x2y3+B,则A=________,B=________.
15、填空:();();
16、已知2m﹣3n=﹣3,则代数式m(n﹣4)﹣n(m﹣6)的值为 .
17、已知a2﹣2a﹣3=0,则代数式3a(a﹣2)的值为 .
18、小明外祖母家的住房装修三年后,地砖出现破损,破损部分的图形如图,现有A、B、C三种地砖可供选择,请问需要A砖 块,B砖 块,C砖 块.
三、解答题
19.计算:
(1)(a+b2﹣c2) (﹣2a2);
;
x (x2﹣x)+2x2(x﹣1).
20.已知有理数a、b、c满足|a﹣b﹣3|+(b+1)2+|c﹣1|=0,求(﹣3ab) (a2c﹣6b2c)的值.
21.某中学扩建教学楼,测量地基时,量得地基长为2a m,宽为(2a﹣24)m,试用a表示地基的面积,并计算当a=25时地基的面积.
22.一条防洪堤坝,其横断面是梯形,上底宽a米,下底宽(a+2b)米,坝高 a米.
(1)求防洪堤坝的横断面积;
(2)如果防洪堤坝长600米,那么这段防洪堤坝的体积是多少立方米
一块长方形硬纸片,长为(5a2+4b2)m,宽为6a4m,在它的四个角上分别剪去一个边长为 m的小正方形,然后折成一个无盖的盒子,请你求这个无盖盒子的表面积.
已知有理数a、b、c满足|a﹣b﹣3|+(b+1)2+|c﹣1|=0,求(﹣3ab) (a2c﹣6b2c)的值.
25.阅读下列文字,并解决问题。
已知x2y=3,求2xy(x5y2-3x3y-4x)的值.
分析:考虑到满足x2y=3的x,y的可能值较多,不可以逐一代入求解,故考虑整体思想,将x2y=3整体代入.
解:2xy(x5y2-3x3y-4x)
=2x6y3-6x4y2-8x2y
=2(x2y)3-6(x2y)2-8x2y,
将x2y=3代入
原式=2×33-6×32-8×3=-24.
请你用上述方法解决下面问题:
已知ab=3,求(2a3b2-3a2b+4a)·(-2b)的值.
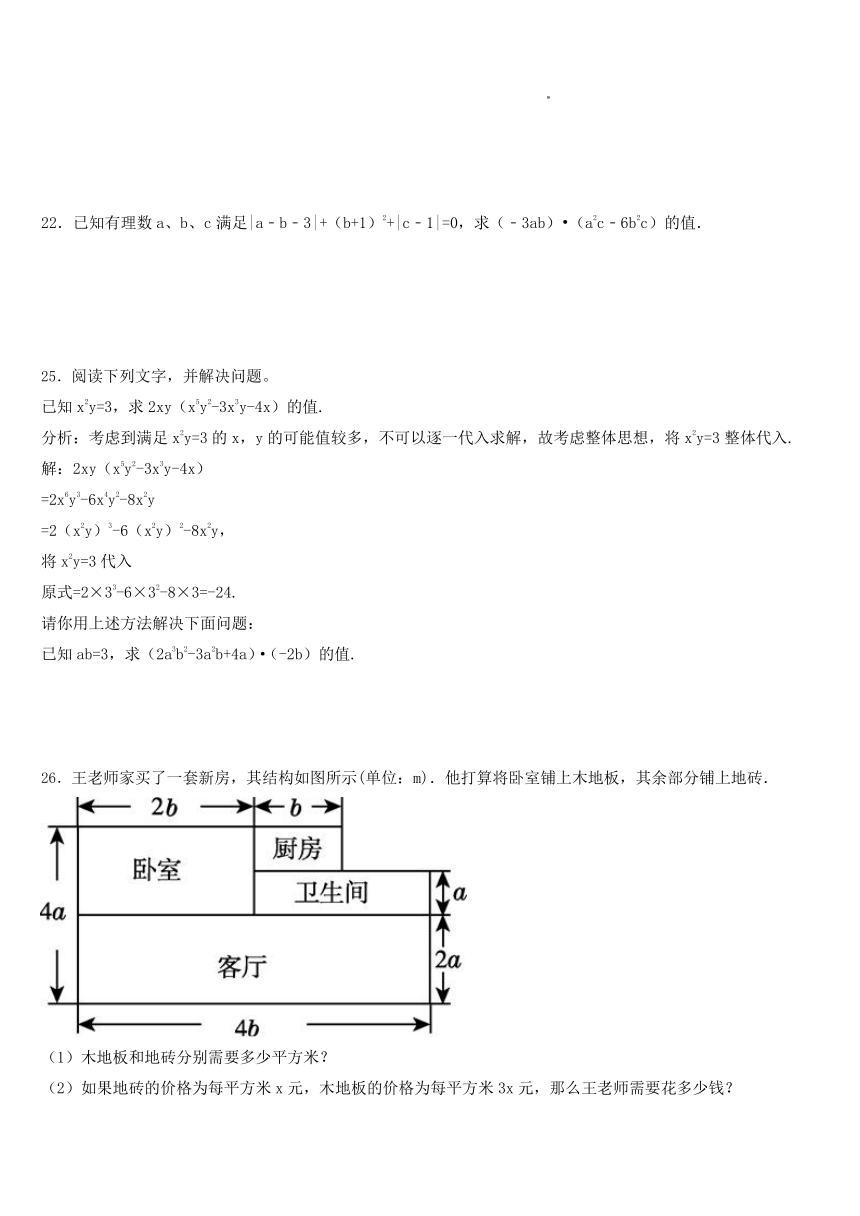
26.王老师家买了一套新房,其结构如图所示(单位:m).他打算将卧室铺上木地板,其余部分铺上地砖.
(1)木地板和地砖分别需要多少平方米?
(2)如果地砖的价格为每平方米x元,木地板的价格为每平方米3x元,那么王老师需要花多少钱?
1、C 2、B 3、A 4、C 5、D 6、A 7、A 8、C 9 D 10. C
11.18x3y4﹣9x2y6 .
12.﹣12.
13. 3,4.
14.6xy3;﹣10xy.
15、;;
16、();();
17、6
18、0
19.【答案】(1)解:(a+b2﹣c2) (﹣2a2)=﹣2a3﹣2a2b2+2a2c2
(2)解: =﹣2x4y2﹣ x3y3+ x2y4
(3)解:x (x2﹣x)+2x2(x﹣1)
=x3﹣x2+2x3﹣2x2
=3x3﹣3x2
单项式乘多项式
20.【答案】解;由|a﹣b﹣3|+(b+1)2+|c﹣1|=0,得 .解得 .
(﹣3ab) (a2c﹣6b2c)=﹣3a3bc+18ab3c,
当 时,原式=﹣3×23×(﹣1)×1+18×2×(﹣1)3×1
=24﹣36
=﹣12
21.【答案】解:根据题意得: 地基的面积是:2a (2a﹣24)=(4a2﹣48a)m2;
当a=25时,
4a2﹣48a=4×252﹣48×25=1300m2
【考点】单项式乘多项式
【分析】根据地基的面积=长乘以宽列出算式,再根据单项式与多项式相乘的法则进行计算,然后把a=25代入即可求出答案.
22.【答案】 (1)解:防洪堤坝的横断面积为: [a+(a+2b)]· a= a(2a+2b)= a2+ ab(平方米)
(2)解:堤坝的体积为:( a2+ ab)×600=300a2+300ab(立方米)
23.【答案】解:纸片的面积是:(5a2+4b2) 6a4=30a6+24a4b2;
小正方形的面积是:( a3)2= a6,
则无盖盒子的表面积是:30a6+24a4b2﹣4× a6=21a6+24a4b2
24.【答案】解;由|a﹣b﹣3|+(b+1)2+|c﹣1|=0,得
.解得 .
(﹣3ab) (a2c﹣6b2c)=﹣3a3bc+18ab3c,
当 时,原式=﹣3×23×(﹣1)×1+18×2×(﹣1)3×1
=24﹣36
=﹣12
25.【答案】解:(2a3b2-3a2b+4a)·(-2b)
=-4a3b3+6a2b2-8ab
=-4(ab)3+6(ab)2-8ab,将ab=3代入,原式=-4×33+6×32-8×3
=-108+54-24=-78
26.【答案】(1)解:卧室的面积是2b(4a-2a)=4ab(m2).
厨房、卫生间、客厅的面积和是b·(4a-2a-a)+a·(4b-2b)+2a·4b=ab+2ab+8ab=11ab(m2),即木地板需要4ab m2,地砖需要11ab m2.
(2)解:11ab·x+4ab·3x=11abx+12abx=23abx(元).
即王老师需要花23abx元
一、单选题
1.计算 的结果为( )
A. B. C. D
2、计算(-8x2)·(5x3-3x2+x)的结果正确的是( )
A.-40x5-24x4-8x3 B.-40x5+24x4-8x3
C.-40x5+24x4+8x3 D.-40x5-24x4+8x3
3、若□×xy=3x2y+2xy,则□内应填的式子是( )
A.3x+2 B.x+2 C.3xy+2 D.xy+2
4、若2x与一个多项式的积为2x3﹣x2+2x,则这个多项式为( )
A.x2﹣2x+1 B.4x2﹣2x+4 C.x2﹣x+1 D.x2﹣x
5.要使(x2+ax+1)(﹣6x3)的展开式中不含x4项,则a应等于( )
A.6 B.﹣1 C. D.0
6.若整式A与单项式﹣a2b的乘积为a(ab3﹣a3b),则整式A为( )
A. a2﹣b2 B. b2﹣a2 C. a2+b2 D. ﹣a2﹣b2
7.今天数学课上,老师讲了单项式乘以多项式,放学后,小华回到家拿出课堂笔记,认真复习老师课上讲的内容,他突然发现一道题;﹣3xy (4y﹣2x﹣1)=﹣12xy2+6x2y+__________,空格的地方被钢笔水弄污了,你认为横线上应填写( )
A. 3xy B. ﹣3xy C. ﹣1 D. 1
8、若要使x(x2+a)+3x﹣2b=x3+5x+4恒成立,则a,b的值分别是( )
A.﹣2,﹣2 B.2,2 C.2,﹣2 D.﹣2,2
9.要使(x3+ax2-x)·(-8x4)的运算结果中不含x6的项,则a的值应为( )
A.8 B.-8 C. D.0
10.如图,边长为 (m + 3)的正方形纸片剪去一个边 长为 m 的正方形之后,余下部分又剪拼成一个长方形(不重叠无缝隙),若拼成的长方形一边长为 3,则此长方形的周长是( )
A.2m + 6 B.4m + 6 C.4m + 12 D.2m + 12
二、填空题
11.计算:(﹣3xy2)2(2x﹣y2)=________.
12.当a=﹣2时,求a2(2a+1)=________.
13.若﹣2x2y(﹣xmy+3xy3)=2x5y2﹣6x3yn , 则m=________,n=________.
14.A、B为单项式,且5x(A﹣2y)=30x2y3+B,则A=________,B=________.
15、填空:();();
16、已知2m﹣3n=﹣3,则代数式m(n﹣4)﹣n(m﹣6)的值为 .
17、已知a2﹣2a﹣3=0,则代数式3a(a﹣2)的值为 .
18、小明外祖母家的住房装修三年后,地砖出现破损,破损部分的图形如图,现有A、B、C三种地砖可供选择,请问需要A砖 块,B砖 块,C砖 块.
三、解答题
19.计算:
(1)(a+b2﹣c2) (﹣2a2);
;
x (x2﹣x)+2x2(x﹣1).
20.已知有理数a、b、c满足|a﹣b﹣3|+(b+1)2+|c﹣1|=0,求(﹣3ab) (a2c﹣6b2c)的值.
21.某中学扩建教学楼,测量地基时,量得地基长为2a m,宽为(2a﹣24)m,试用a表示地基的面积,并计算当a=25时地基的面积.
22.一条防洪堤坝,其横断面是梯形,上底宽a米,下底宽(a+2b)米,坝高 a米.
(1)求防洪堤坝的横断面积;
(2)如果防洪堤坝长600米,那么这段防洪堤坝的体积是多少立方米
一块长方形硬纸片,长为(5a2+4b2)m,宽为6a4m,在它的四个角上分别剪去一个边长为 m的小正方形,然后折成一个无盖的盒子,请你求这个无盖盒子的表面积.
已知有理数a、b、c满足|a﹣b﹣3|+(b+1)2+|c﹣1|=0,求(﹣3ab) (a2c﹣6b2c)的值.
25.阅读下列文字,并解决问题。
已知x2y=3,求2xy(x5y2-3x3y-4x)的值.
分析:考虑到满足x2y=3的x,y的可能值较多,不可以逐一代入求解,故考虑整体思想,将x2y=3整体代入.
解:2xy(x5y2-3x3y-4x)
=2x6y3-6x4y2-8x2y
=2(x2y)3-6(x2y)2-8x2y,
将x2y=3代入
原式=2×33-6×32-8×3=-24.
请你用上述方法解决下面问题:
已知ab=3,求(2a3b2-3a2b+4a)·(-2b)的值.
26.王老师家买了一套新房,其结构如图所示(单位:m).他打算将卧室铺上木地板,其余部分铺上地砖.
(1)木地板和地砖分别需要多少平方米?
(2)如果地砖的价格为每平方米x元,木地板的价格为每平方米3x元,那么王老师需要花多少钱?
1、C 2、B 3、A 4、C 5、D 6、A 7、A 8、C 9 D 10. C
11.18x3y4﹣9x2y6 .
12.﹣12.
13. 3,4.
14.6xy3;﹣10xy.
15、;;
16、();();
17、6
18、0
19.【答案】(1)解:(a+b2﹣c2) (﹣2a2)=﹣2a3﹣2a2b2+2a2c2
(2)解: =﹣2x4y2﹣ x3y3+ x2y4
(3)解:x (x2﹣x)+2x2(x﹣1)
=x3﹣x2+2x3﹣2x2
=3x3﹣3x2
单项式乘多项式
20.【答案】解;由|a﹣b﹣3|+(b+1)2+|c﹣1|=0,得 .解得 .
(﹣3ab) (a2c﹣6b2c)=﹣3a3bc+18ab3c,
当 时,原式=﹣3×23×(﹣1)×1+18×2×(﹣1)3×1
=24﹣36
=﹣12
21.【答案】解:根据题意得: 地基的面积是:2a (2a﹣24)=(4a2﹣48a)m2;
当a=25时,
4a2﹣48a=4×252﹣48×25=1300m2
【考点】单项式乘多项式
【分析】根据地基的面积=长乘以宽列出算式,再根据单项式与多项式相乘的法则进行计算,然后把a=25代入即可求出答案.
22.【答案】 (1)解:防洪堤坝的横断面积为: [a+(a+2b)]· a= a(2a+2b)= a2+ ab(平方米)
(2)解:堤坝的体积为:( a2+ ab)×600=300a2+300ab(立方米)
23.【答案】解:纸片的面积是:(5a2+4b2) 6a4=30a6+24a4b2;
小正方形的面积是:( a3)2= a6,
则无盖盒子的表面积是:30a6+24a4b2﹣4× a6=21a6+24a4b2
24.【答案】解;由|a﹣b﹣3|+(b+1)2+|c﹣1|=0,得
.解得 .
(﹣3ab) (a2c﹣6b2c)=﹣3a3bc+18ab3c,
当 时,原式=﹣3×23×(﹣1)×1+18×2×(﹣1)3×1
=24﹣36
=﹣12
25.【答案】解:(2a3b2-3a2b+4a)·(-2b)
=-4a3b3+6a2b2-8ab
=-4(ab)3+6(ab)2-8ab,将ab=3代入,原式=-4×33+6×32-8×3
=-108+54-24=-78
26.【答案】(1)解:卧室的面积是2b(4a-2a)=4ab(m2).
厨房、卫生间、客厅的面积和是b·(4a-2a-a)+a·(4b-2b)+2a·4b=ab+2ab+8ab=11ab(m2),即木地板需要4ab m2,地砖需要11ab m2.
(2)解:11ab·x+4ab·3x=11abx+12abx=23abx(元).
即王老师需要花23abx元
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
