2021—2022学年人教版数学八年级下册18.2.3 正方形的判定巩固提升练习(word版含答案)
文档属性
| 名称 | 2021—2022学年人教版数学八年级下册18.2.3 正方形的判定巩固提升练习(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 324.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 09:32:00 | ||
图片预览



文档简介
18.2.3 正方形的判定巩固提升练习
1. 四边形是平行四边形,对角线,相交于点,则下列结论错误的是( )
A.当时,四边形是矩形
B.当平分时,四边形是菱形
C.当时,四边形是矩形
D.当且时,四边形是正方形
2. 如图,把一个长方形纸片对折两次,然后剪下一个角再展开,要使展开所得的四边形是正方形,那么剪口(图中虚线)应与折痕成多少度的角( )
A. B. C. D.
3. 如图,已知四边形是平行四边形,下列结论中错误的是( )
A.当时,它是菱形
B.当时,它是菱形
C.当时,它是矩形
D.当时,它是正方形
4. 如图,在中,,为的中点,连接,在线段的延长线上取点,使得,连接,.下列说法错误的是( )
A.四边形一定是平行四边形
B.四边形可能是菱形
C.四边形一定是矩形
D.四边形一定是正方形
5. 已知四边形是平行四边形,再从下列四个条件中,选两个作为补充条件,使得四边形是正方形,现有下列四种选法,其中错误的是( )
①;②;③;④.
A.选①② B.选①③ C.选②③ D.选②④
6. 如图,在任意四边形中,,,,分别是,,,的中点,对于四边形的形状,以下结论中,错误的是( )
A.当时,四边形为正方形
B.当时,四边形为菱形
C.当时,四边形为矩形
D.四边形一定为平行四边形
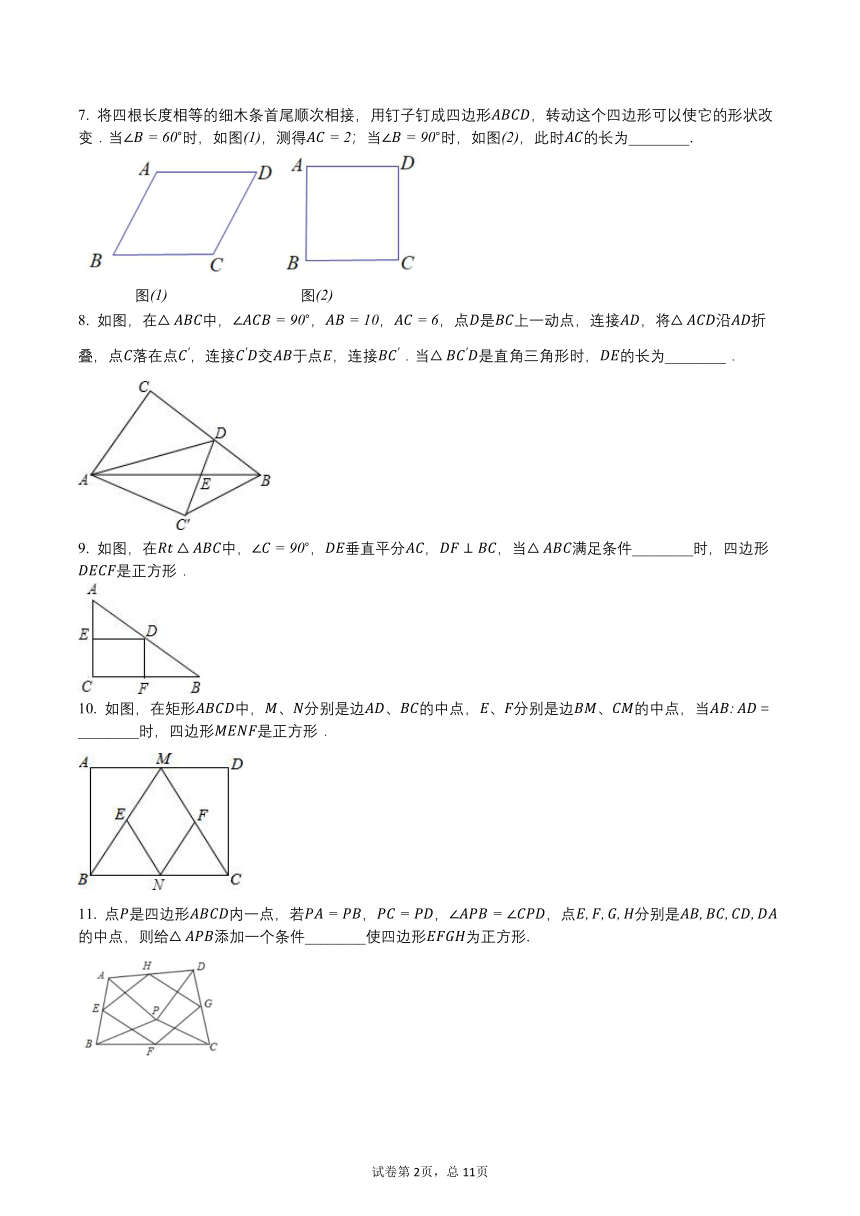
7. 将四根长度相等的细木条首尾顺次相接,用钉子钉成四边形,转动这个四边形可以使它的形状改变.当时,如图,测得;当时,如图,此时的长为________.
图 图
8. 如图,在中,,,,点是上一动点,连接,将沿折叠,点落在点,连接交于点,连接.当是直角三角形时,的长为________.
9. 如图,在中,,垂直平分,,当满足条件________时,四边形是正方形.
10. 如图,在矩形中,、分别是边、的中点,、分别是边、的中点,当=________时,四边形是正方形.
11. 点是四边形内一点,若,,,点分别是的中点,则给添加一个条件________使四边形为正方形.
12. 如图,在正方形的内侧,作等边 ,则的度数是________.
13. 已知:如图,在平行四边形中,对角线与相交于点,点为的中点,连接,的延长线交的延长线于点,连接.
求证: ;
若,,判断四边形的形状,并证明你的结论.
14. 如图,在中,,过点的直线,为边上一点,过点作,交直线于,垂足为,连接,.
求证:;
当在中点时,四边形是什么特殊四边形?说明理由;
在满足的条件下,当满足什么条件时,四边形是正方形?说明理由.
15. 如图,、、、分别是四边形四条边的中点.
试判定四边形的形状,并说明理由;
四边形的对角线满足什么条件,可使四边形为矩形,说明理由;
四边形的对角线满足什么条件,可使四边形为菱形,说明理由;
四边形的对角线满足什么条件,可使四边形为正方形,请说明理由.
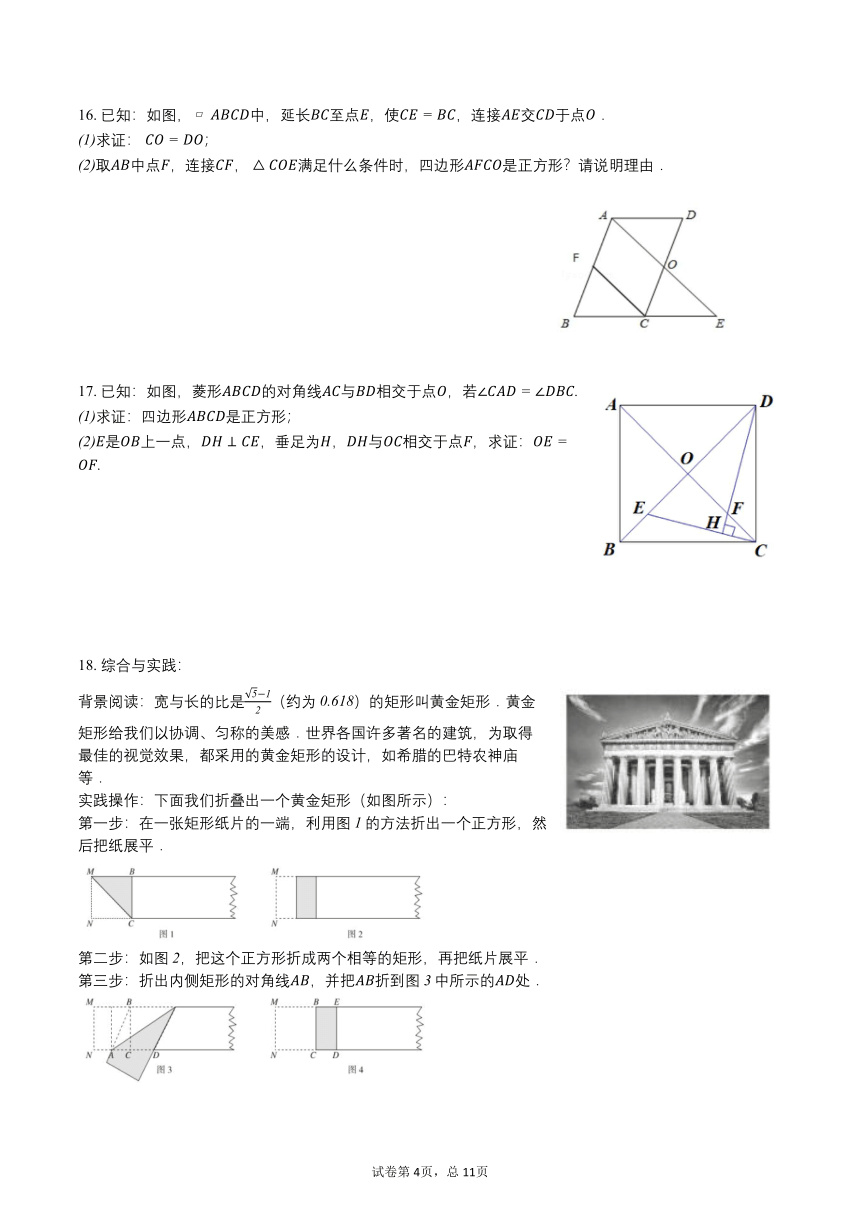
16. 已知:如图, 中,延长至点,使,连接交于点.
求证: ;
取中点,连接, 满足什么条件时,四边形是正方形?请说明理由.
17. 已知:如图,菱形的对角线与相交于点,若
求证:四边形是正方形;
是上一点,,垂足为,与相交于点,求证:
18. 综合与实践:
背景阅读:宽与长的比是(约为)的矩形叫黄金矩形.黄金矩形给我们以协调、匀称的美感.世界各国许多著名的建筑,为取得最佳的视觉效果,都采用的黄金矩形的设计,如希腊的巴特农神庙等.
实践操作:下面我们折叠出一个黄金矩形(如图所示):
第一步:在一张矩形纸片的一端,利用图的方法折出一个正方形,然后把纸展平.
第二步:如图,把这个正方形折成两个相等的矩形,再把纸片展平.
第三步:折出内侧矩形的对角线,并把折到图中所示的处.
第四步:展平纸片,按照所得的点折出,矩形(图)就是黄金矩形.
问题解决:
请在图中证明四边形是正方形;
若,请通过计算来说明矩形是黄金矩形.
19. 综合与实践
问题情境:
在数学活动课上,老师出示了这样一个问题:如图,点为正方形内一点, ,将绕点按逆时针方向旋转 ,得到(点的对应点为点).延长交于点,连接,.试判断四边形的形状.
探究展示:
勤奋小组发现四边形的形状是正方形,并展示了如下的证明方法:
证明:由旋转可知:
,________,
又∵ ,,
∴ ,
∴ 四边形是矩形(依据)
由旋转可知,________,
∴ 四边形是正方形.(依据)
图 图
解决问题:
请你将上述证明过程补充完整,并写出“依据”“依据”分别是指什么?
智慧小组还发现:若, ,还可以求出的长度,请你写出求解过程;
创新小组受到智慧小组的启发,继续进行探究,发现:如图,当时,可以求出的度数,请你帮创新小组解决这个问题.
参考答案与试题解析
一、 选择题
1.
【答案】
C
2.
【答案】
B
3.
【答案】
D
4.
【答案】
D
5.
【答案】
C
6.
【答案】
A
二、 填空题
7.
【答案】
8.
【答案】
或
9.
【答案】
(或)
10.
【答案】
11.
【答案】
是等腰直角三角形
12.
【答案】
三、 解答题
13.
【答案】
证明:四边形是平行四边形,
,即,
,,
点是的中点,
,
在和中,
.
解:四边形是正方形.
证明:∵ 四边形是平行四边形,
∴ .
又∵ ,
∴ .
由知:,
,
四边形是平行四边形,
,即,
四边形是平行四边形,
又∵ ,
∴ 四边形为菱形.
,
,
,
,
四边形是正方形.
14.
【答案】
证明:∵ ,
∴ ,
∵ ,
∴ ,
∴ ,
∵ ,即,
∴ 四边形是平行四边形,
∴ .
解:四边形是菱形,理由如下:
∵ 为中点,
∴ ,
∵ ,
∴ ,
∵ ,
∴ 四边形是平行四边形,
∵ ,为中点,
∴ ,
∴ 四边形是菱形.
解:当是等腰直角三角形时,四边形是正方形,理由如下:
∵ ,,为的中点,
∴ ,
∴ ,
∴ 四边形是正方形.
15.
【答案】
解:四边形是平行四边形,
证明:连接,如图,
、分别是、的中点,
是的中位线,
,,
同理: ,
四边形为平行四边形.
四边形的对角线互相垂直时,四边形是矩形;
理由:若,则 平行四边形是矩形.
四边形的对角线相等时,四边形是菱形;
理由:若,则 平行四边形是菱形.
四边形的对角线相等且互相垂直时,四边形是正方形.
理由:若,且,则 平行四边形是正方形.
16.
【答案】
证明:∵ 四边形是平行四边形,
∴ ,,
∴ ,
,
∴ .
又∵ ,
∴ ,
∴ .
解:, ,四边形是正方形.
∵ ,
∴ .
又∵ 是的中点,
∴ .
∵ 四边形是平行四边形,
∴ ,,
∴ ,,
∴ 四边形是平行四边形.
∵ ,
∴ .
∵ ,
∴
∴ 平行四边形是菱形.
∵ ,
∴ 菱形是正方形.
17.
【答案】
证明:∵ 四边形是菱形,
∴ ,,,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∴ 四边形是正方形.
∵ 四边形是正方形,
∴ ,,,,
∴ ,,
∵ ,垂足为,
,,
又,
,
,
.
18.
【答案】
解:由矩形性质可知,
由折叠可知,,
∴ ,
∴ 四边形是矩形.
又∵ ,
∴ 矩形是正方形.
∵ ,∴ .
在中,.
由折叠知,
∴ .
又∵ ,
∴ .
∴ 矩开为黄金矩形.
19.
【答案】
解:由旋转可知:,,
又,,
,
四边形是矩形.(依据)
由旋转可知,,
四边形是正方形.(依据)
依据:有三个角是直角的四边形是矩形
依据:有一组邻边相等的矩形是正方形.
设,
∵ 四边形是正方形,
,,
在中,,
,
解得(舍得),.
的长为.
,
, ,
.
.试卷第4页,总9页
试卷第5页,总9页
1. 四边形是平行四边形,对角线,相交于点,则下列结论错误的是( )
A.当时,四边形是矩形
B.当平分时,四边形是菱形
C.当时,四边形是矩形
D.当且时,四边形是正方形
2. 如图,把一个长方形纸片对折两次,然后剪下一个角再展开,要使展开所得的四边形是正方形,那么剪口(图中虚线)应与折痕成多少度的角( )
A. B. C. D.
3. 如图,已知四边形是平行四边形,下列结论中错误的是( )
A.当时,它是菱形
B.当时,它是菱形
C.当时,它是矩形
D.当时,它是正方形
4. 如图,在中,,为的中点,连接,在线段的延长线上取点,使得,连接,.下列说法错误的是( )
A.四边形一定是平行四边形
B.四边形可能是菱形
C.四边形一定是矩形
D.四边形一定是正方形
5. 已知四边形是平行四边形,再从下列四个条件中,选两个作为补充条件,使得四边形是正方形,现有下列四种选法,其中错误的是( )
①;②;③;④.
A.选①② B.选①③ C.选②③ D.选②④
6. 如图,在任意四边形中,,,,分别是,,,的中点,对于四边形的形状,以下结论中,错误的是( )
A.当时,四边形为正方形
B.当时,四边形为菱形
C.当时,四边形为矩形
D.四边形一定为平行四边形
7. 将四根长度相等的细木条首尾顺次相接,用钉子钉成四边形,转动这个四边形可以使它的形状改变.当时,如图,测得;当时,如图,此时的长为________.
图 图
8. 如图,在中,,,,点是上一动点,连接,将沿折叠,点落在点,连接交于点,连接.当是直角三角形时,的长为________.
9. 如图,在中,,垂直平分,,当满足条件________时,四边形是正方形.
10. 如图,在矩形中,、分别是边、的中点,、分别是边、的中点,当=________时,四边形是正方形.
11. 点是四边形内一点,若,,,点分别是的中点,则给添加一个条件________使四边形为正方形.
12. 如图,在正方形的内侧,作等边 ,则的度数是________.
13. 已知:如图,在平行四边形中,对角线与相交于点,点为的中点,连接,的延长线交的延长线于点,连接.
求证: ;
若,,判断四边形的形状,并证明你的结论.
14. 如图,在中,,过点的直线,为边上一点,过点作,交直线于,垂足为,连接,.
求证:;
当在中点时,四边形是什么特殊四边形?说明理由;
在满足的条件下,当满足什么条件时,四边形是正方形?说明理由.
15. 如图,、、、分别是四边形四条边的中点.
试判定四边形的形状,并说明理由;
四边形的对角线满足什么条件,可使四边形为矩形,说明理由;
四边形的对角线满足什么条件,可使四边形为菱形,说明理由;
四边形的对角线满足什么条件,可使四边形为正方形,请说明理由.
16. 已知:如图, 中,延长至点,使,连接交于点.
求证: ;
取中点,连接, 满足什么条件时,四边形是正方形?请说明理由.
17. 已知:如图,菱形的对角线与相交于点,若
求证:四边形是正方形;
是上一点,,垂足为,与相交于点,求证:
18. 综合与实践:
背景阅读:宽与长的比是(约为)的矩形叫黄金矩形.黄金矩形给我们以协调、匀称的美感.世界各国许多著名的建筑,为取得最佳的视觉效果,都采用的黄金矩形的设计,如希腊的巴特农神庙等.
实践操作:下面我们折叠出一个黄金矩形(如图所示):
第一步:在一张矩形纸片的一端,利用图的方法折出一个正方形,然后把纸展平.
第二步:如图,把这个正方形折成两个相等的矩形,再把纸片展平.
第三步:折出内侧矩形的对角线,并把折到图中所示的处.
第四步:展平纸片,按照所得的点折出,矩形(图)就是黄金矩形.
问题解决:
请在图中证明四边形是正方形;
若,请通过计算来说明矩形是黄金矩形.
19. 综合与实践
问题情境:
在数学活动课上,老师出示了这样一个问题:如图,点为正方形内一点, ,将绕点按逆时针方向旋转 ,得到(点的对应点为点).延长交于点,连接,.试判断四边形的形状.
探究展示:
勤奋小组发现四边形的形状是正方形,并展示了如下的证明方法:
证明:由旋转可知:
,________,
又∵ ,,
∴ ,
∴ 四边形是矩形(依据)
由旋转可知,________,
∴ 四边形是正方形.(依据)
图 图
解决问题:
请你将上述证明过程补充完整,并写出“依据”“依据”分别是指什么?
智慧小组还发现:若, ,还可以求出的长度,请你写出求解过程;
创新小组受到智慧小组的启发,继续进行探究,发现:如图,当时,可以求出的度数,请你帮创新小组解决这个问题.
参考答案与试题解析
一、 选择题
1.
【答案】
C
2.
【答案】
B
3.
【答案】
D
4.
【答案】
D
5.
【答案】
C
6.
【答案】
A
二、 填空题
7.
【答案】
8.
【答案】
或
9.
【答案】
(或)
10.
【答案】
11.
【答案】
是等腰直角三角形
12.
【答案】
三、 解答题
13.
【答案】
证明:四边形是平行四边形,
,即,
,,
点是的中点,
,
在和中,
.
解:四边形是正方形.
证明:∵ 四边形是平行四边形,
∴ .
又∵ ,
∴ .
由知:,
,
四边形是平行四边形,
,即,
四边形是平行四边形,
又∵ ,
∴ 四边形为菱形.
,
,
,
,
四边形是正方形.
14.
【答案】
证明:∵ ,
∴ ,
∵ ,
∴ ,
∴ ,
∵ ,即,
∴ 四边形是平行四边形,
∴ .
解:四边形是菱形,理由如下:
∵ 为中点,
∴ ,
∵ ,
∴ ,
∵ ,
∴ 四边形是平行四边形,
∵ ,为中点,
∴ ,
∴ 四边形是菱形.
解:当是等腰直角三角形时,四边形是正方形,理由如下:
∵ ,,为的中点,
∴ ,
∴ ,
∴ 四边形是正方形.
15.
【答案】
解:四边形是平行四边形,
证明:连接,如图,
、分别是、的中点,
是的中位线,
,,
同理: ,
四边形为平行四边形.
四边形的对角线互相垂直时,四边形是矩形;
理由:若,则 平行四边形是矩形.
四边形的对角线相等时,四边形是菱形;
理由:若,则 平行四边形是菱形.
四边形的对角线相等且互相垂直时,四边形是正方形.
理由:若,且,则 平行四边形是正方形.
16.
【答案】
证明:∵ 四边形是平行四边形,
∴ ,,
∴ ,
,
∴ .
又∵ ,
∴ ,
∴ .
解:, ,四边形是正方形.
∵ ,
∴ .
又∵ 是的中点,
∴ .
∵ 四边形是平行四边形,
∴ ,,
∴ ,,
∴ 四边形是平行四边形.
∵ ,
∴ .
∵ ,
∴
∴ 平行四边形是菱形.
∵ ,
∴ 菱形是正方形.
17.
【答案】
证明:∵ 四边形是菱形,
∴ ,,,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∴ 四边形是正方形.
∵ 四边形是正方形,
∴ ,,,,
∴ ,,
∵ ,垂足为,
,,
又,
,
,
.
18.
【答案】
解:由矩形性质可知,
由折叠可知,,
∴ ,
∴ 四边形是矩形.
又∵ ,
∴ 矩形是正方形.
∵ ,∴ .
在中,.
由折叠知,
∴ .
又∵ ,
∴ .
∴ 矩开为黄金矩形.
19.
【答案】
解:由旋转可知:,,
又,,
,
四边形是矩形.(依据)
由旋转可知,,
四边形是正方形.(依据)
依据:有三个角是直角的四边形是矩形
依据:有一组邻边相等的矩形是正方形.
设,
∵ 四边形是正方形,
,,
在中,,
,
解得(舍得),.
的长为.
,
, ,
.
.试卷第4页,总9页
试卷第5页,总9页
