2021-2022学年人教版下册八年级数学18.2.3 正方形性质与判定 综合运用 (word版含答案)
文档属性
| 名称 | 2021-2022学年人教版下册八年级数学18.2.3 正方形性质与判定 综合运用 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 428.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 09:33:22 | ||
图片预览


文档简介
18.2.3 正方形性质与判定综合运用二
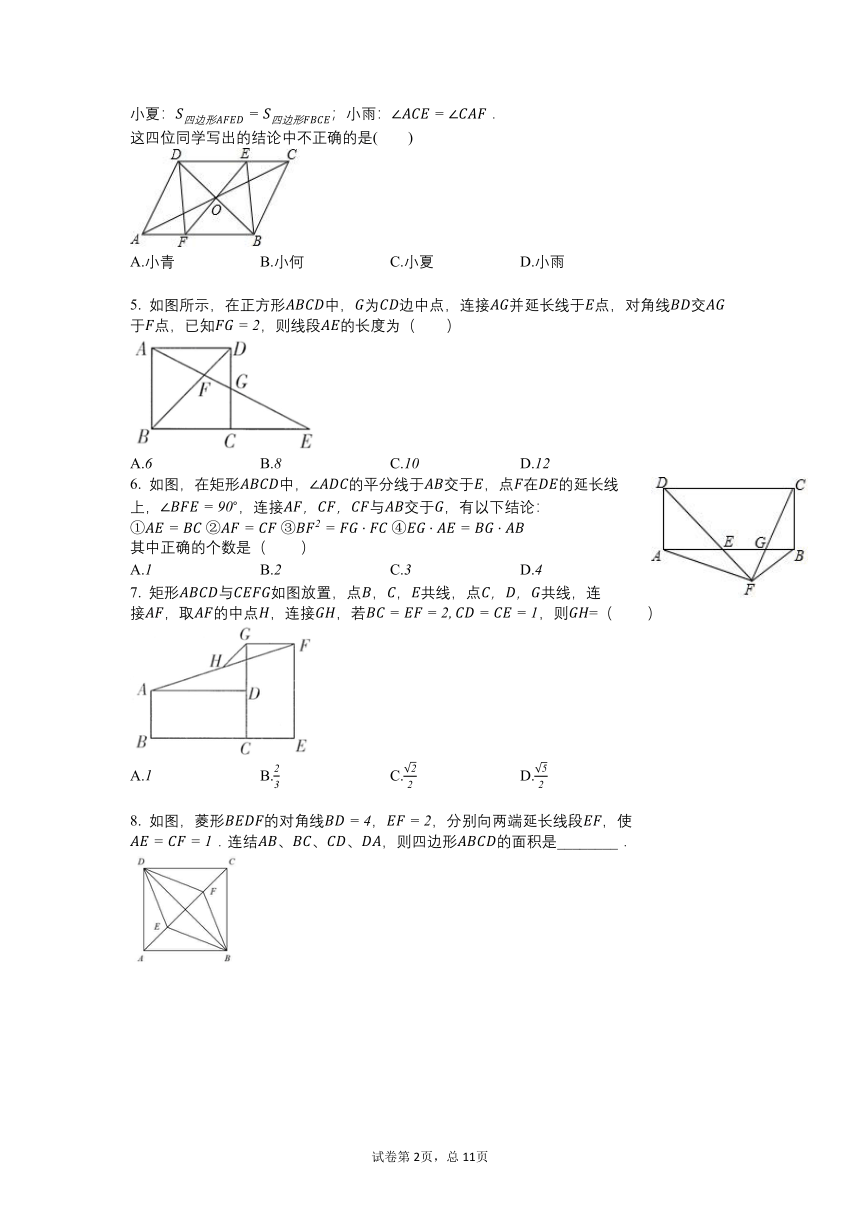
1. 如图,在四边形中,,,,交于点.添加一个条件使这个四边形成为一种特殊的平行四边形,则以下说法错误的是( )
A.添加“”,则四边形是矩形
B.添加“”,则四边形是菱形
C.添加“”,则四边形是菱形
D.添加“”,则四边形是正方形
2. 将图中两个三角形按图所示的方式摆放,其中四边形为矩形,分别连接,,甲、乙两人有如下结论:
甲:若四边形为正方形,则四边形必是正方形;
乙:若四边形为正方形,则四边形必是正方形.
下列判断正确的是()
A.甲正确,乙不正确 B.甲不正确,乙正确
C.甲、乙都不正确 D.甲、乙都正确
3. 如图,在中,点,,分别在边,,上,且,,下列四个判断中,不正确的是( )
A.四边形是平行四边形
B.如果,那么四边形是矩形
C.如果平分,那么四边形是菱形
D.如果且,那么四边形是正方形
4. 在一次数学课上,张老师出示了一个题目:“如图, 的对角线相交于点,过点作垂直于交,分别于点,,连接,.请根据上述条件,写出一个正确结论.”其中四位同学写出的结论如下:
小青:;小何:四边形是正方形;
小夏:;小雨:.
这四位同学写出的结论中不正确的是( )
A.小青 B.小何 C.小夏 D.小雨
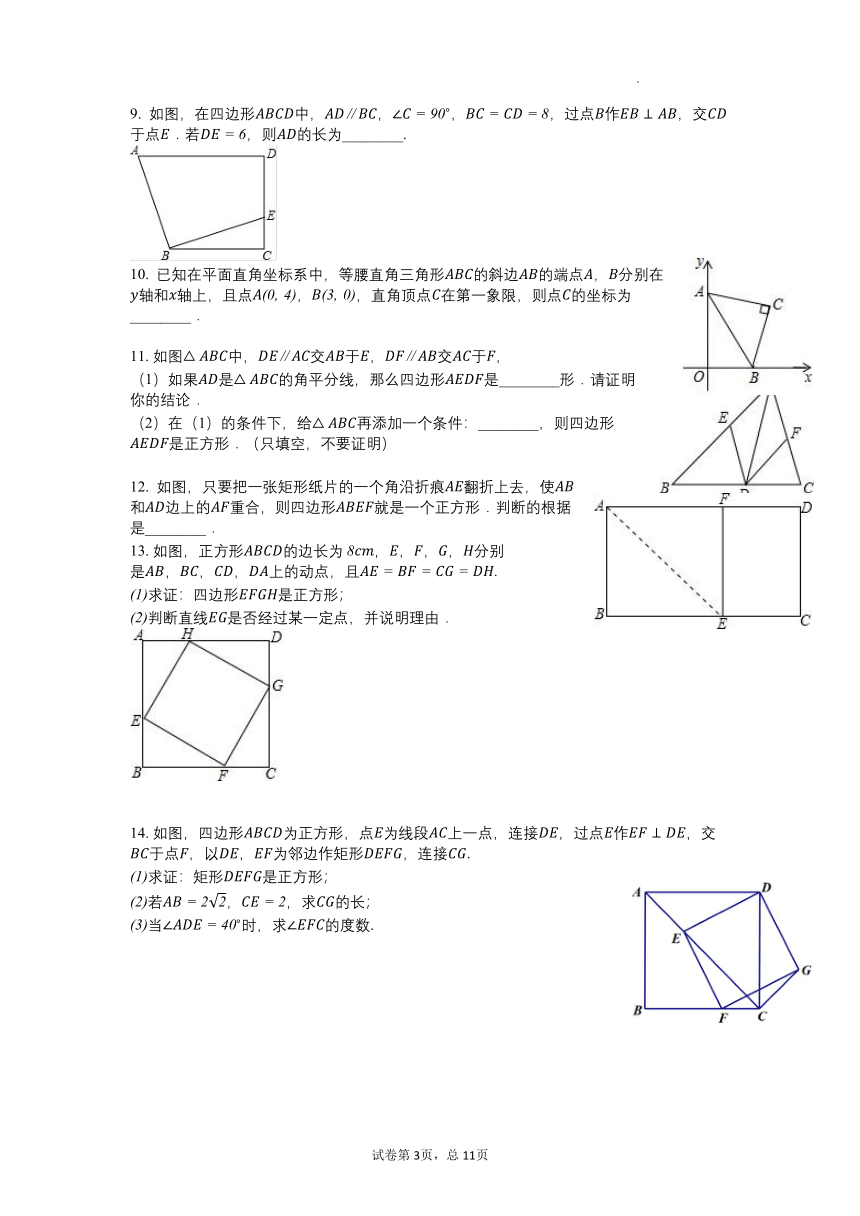
5. 如图所示,在正方形中,为边中点,连接并延长线于点,对角线交于点,已知,则线段的长度为( )
A. B. C. D.
6. 如图,在矩形中,的平分线于交于,点在的延长线上,,连接与交于,有以下结论:
① ② ③ ④
其中正确的个数是( )
A. B. C. D.
7. 矩形与如图放置,点,,共线,点共线,连接,取的中点,连接,若,则=( )
A. B. C. D.
8. 如图,菱形的对角线,,分别向两端延长线段,使.连结、、、,则四边形的面积是________.
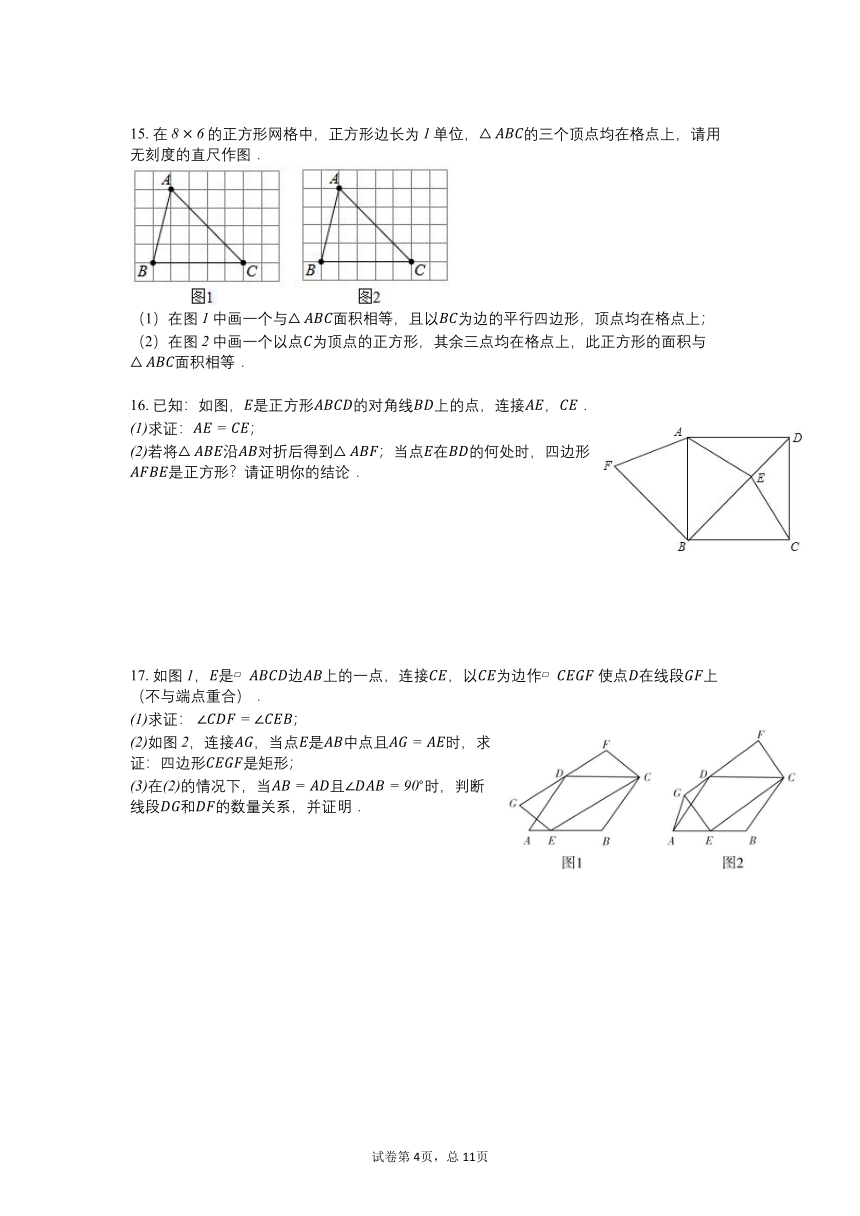
9. 如图,在四边形中,,,,过点作,交于点.若,则的长为________.
10. 已知在平面直角坐标系中,等腰直角三角形的斜边的端点,分别在轴和轴上,且点,,直角顶点在第一象限,则点的坐标为________.
11. 如图中,交于,交于,
(1)如果是的角平分线,那么四边形是________形.请证明你的结论.
(2)在(1)的条件下,给再添加一个条件:________,则四边形是正方形.(只填空,不要证明)
12. 如图,只要把一张矩形纸片的一个角沿折痕翻折上去,使和边上的重合,则四边形就是一个正方形.判断的根据是________.
13. 如图,正方形的边长为,,,,分别是,,,上的动点,且
求证:四边形是正方形;
判断直线是否经过某一定点,并说明理由.
14. 如图,四边形为正方形,点为线段上一点,连接,过点作,交于点,以,为邻边作矩形,连接.
求证:矩形是正方形;
若,,求的长;
当时,求的度数.
15. 在的正方形网格中,正方形边长为单位,的三个顶点均在格点上,请用无刻度的直尺作图.
(1)在图中画一个与面积相等,且以为边的平行四边形,顶点均在格点上;
(2)在图中画一个以点为顶点的正方形,其余三点均在格点上,此正方形的面积与面积相等.
16. 已知:如图,是正方形的对角线上的点,连接,.
求证:;
若将沿对折后得到;当点在的何处时,四边形是正方形?请证明你的结论.
17. 如图,是 边上的一点,连接,以为边作 使点在线段上(不与端点重合).
求证: ;
如图,连接,当点是中点且时,求证:四边形是矩形;
在的情况下,当且时,判断线段和的数量关系,并证明.
18. 在 中,的平分线交于点,交的延长线于点,分别过点,作,.
如图,求证:四边形是菱形;
如图,连接,,与相交于点,若,求证:;
如图,连接交于点,连接,若,,,直接写出的长.
参考答案与试题解析
一、 选择题
1.
【答案】
A
2.
【答案】
B
3.
【答案】
D
4.
【答案】
B
5.
【答案】
D
6.
【答案】
C
7.
【答案】
C
二、 填空题
8.
【答案】
9.
【答案】
10.
【答案】
11.
【答案】
(1)菱形,
证明:∵ ,,
∴ 四边形是平行四边形.
∵
∴
又∵
∴
∴
∴ □是菱形;
(2),
理由如下:∵ 四边形是菱形,,
∴ 四边形是正方形.
12.
【答案】
有一组邻边相等的矩形是正方形
三、 解答题
13.
【答案】
证明:∵ ,
,
∵ ,
∴ ,
∴ ,
∴ ,,
∴ 四边形是菱形.
∴ ,,
∴ ,
∴ ,
∵ 四边形是菱形,,
∴ 四边形是正方形.
解:直线经过正方形的中心,理由如下:
连接交于点.
∵ 四边形是正方形.
∴ ,
∴ ,
∵ ,,,
∴ ,
∴ ,即点为的中点.
∴ 直线经过正方形的中心.
14.
【答案】
证明:过点作于,于,如图,
∵ 四边形为正方形,
.
,,
,.
∵ ,,
∴ .
在和中,
∴ ,
∴ ,
∴ 矩形是正方形.
解:如图,
在中,,
∵ ,
∴ ,
∴ 点与重合,此时是等腰直角三角形,
.
解:当时,
,
∵ ,
∴ .
∵ ,
∴ ,
15.
【答案】
如图所示:平行四边形即为所求;
如图所示:正方形即为所求.
16.
【答案】
证明:∵ 四边形是正方形,
∴ ,,
,
在和中,
∴ ,
∴ .
解:点在的中点时,四边形是正方形.
理由如下:
由折叠的性质得:,
,,
∵ ,是的中点,
∴ ,
∵ ,
∴ ,
∴ 四边形是菱形,是正方形对角线的交点,
∴ ,
∴ ,
∴ 四边形是正方形.
17.
【答案】
证明:∵ 四边形与四边形是平行四边形,
∴ ,
∴ ,,
∴ .
证明:延长,交于点.
∵ 四边形是平行四边形,
∴ ,
∵ 是中点,
∴ .
∵ ,,
∴ 四边形是平行四边形,
∴ ,
∴ ,
∴ .
∵ ,
∴ ,,
∴ .
在中,,
即,
∴ ,
∴ ,
∵ 四边形是平行四边形,
∴ 平行四边形是矩形.
解:,理由如下:
连接,设,
∵ ,,
四边形为平行四边形,
∴ 平行四边形是正方形,
∴ ,, ,
在和中,
,
,
∵ 四边形是矩形,
∴ ,,
由得,在平行四边中,
,.
,
∴ ,
在中,,
∴ ,
∴ .
18.
【答案】
证明:,,
四边形是平行四边形.
,.
,.
平分,,
,,
四边形是菱形.
证明:由知四边形是菱形,
,.
,
,
四边形是平行四边形,
.
,
.
,
.
,
,
,
.
解:,
四边形是矩形,
,
,
菱形是正方形,
.
,
,
,
.
同理,,则.
如图,过点作于点,
则,
,
.试卷第4页,总9页
试卷第5页,总9页
1. 如图,在四边形中,,,,交于点.添加一个条件使这个四边形成为一种特殊的平行四边形,则以下说法错误的是( )
A.添加“”,则四边形是矩形
B.添加“”,则四边形是菱形
C.添加“”,则四边形是菱形
D.添加“”,则四边形是正方形
2. 将图中两个三角形按图所示的方式摆放,其中四边形为矩形,分别连接,,甲、乙两人有如下结论:
甲:若四边形为正方形,则四边形必是正方形;
乙:若四边形为正方形,则四边形必是正方形.
下列判断正确的是()
A.甲正确,乙不正确 B.甲不正确,乙正确
C.甲、乙都不正确 D.甲、乙都正确
3. 如图,在中,点,,分别在边,,上,且,,下列四个判断中,不正确的是( )
A.四边形是平行四边形
B.如果,那么四边形是矩形
C.如果平分,那么四边形是菱形
D.如果且,那么四边形是正方形
4. 在一次数学课上,张老师出示了一个题目:“如图, 的对角线相交于点,过点作垂直于交,分别于点,,连接,.请根据上述条件,写出一个正确结论.”其中四位同学写出的结论如下:
小青:;小何:四边形是正方形;
小夏:;小雨:.
这四位同学写出的结论中不正确的是( )
A.小青 B.小何 C.小夏 D.小雨
5. 如图所示,在正方形中,为边中点,连接并延长线于点,对角线交于点,已知,则线段的长度为( )
A. B. C. D.
6. 如图,在矩形中,的平分线于交于,点在的延长线上,,连接与交于,有以下结论:
① ② ③ ④
其中正确的个数是( )
A. B. C. D.
7. 矩形与如图放置,点,,共线,点共线,连接,取的中点,连接,若,则=( )
A. B. C. D.
8. 如图,菱形的对角线,,分别向两端延长线段,使.连结、、、,则四边形的面积是________.
9. 如图,在四边形中,,,,过点作,交于点.若,则的长为________.
10. 已知在平面直角坐标系中,等腰直角三角形的斜边的端点,分别在轴和轴上,且点,,直角顶点在第一象限,则点的坐标为________.
11. 如图中,交于,交于,
(1)如果是的角平分线,那么四边形是________形.请证明你的结论.
(2)在(1)的条件下,给再添加一个条件:________,则四边形是正方形.(只填空,不要证明)
12. 如图,只要把一张矩形纸片的一个角沿折痕翻折上去,使和边上的重合,则四边形就是一个正方形.判断的根据是________.
13. 如图,正方形的边长为,,,,分别是,,,上的动点,且
求证:四边形是正方形;
判断直线是否经过某一定点,并说明理由.
14. 如图,四边形为正方形,点为线段上一点,连接,过点作,交于点,以,为邻边作矩形,连接.
求证:矩形是正方形;
若,,求的长;
当时,求的度数.
15. 在的正方形网格中,正方形边长为单位,的三个顶点均在格点上,请用无刻度的直尺作图.
(1)在图中画一个与面积相等,且以为边的平行四边形,顶点均在格点上;
(2)在图中画一个以点为顶点的正方形,其余三点均在格点上,此正方形的面积与面积相等.
16. 已知:如图,是正方形的对角线上的点,连接,.
求证:;
若将沿对折后得到;当点在的何处时,四边形是正方形?请证明你的结论.
17. 如图,是 边上的一点,连接,以为边作 使点在线段上(不与端点重合).
求证: ;
如图,连接,当点是中点且时,求证:四边形是矩形;
在的情况下,当且时,判断线段和的数量关系,并证明.
18. 在 中,的平分线交于点,交的延长线于点,分别过点,作,.
如图,求证:四边形是菱形;
如图,连接,,与相交于点,若,求证:;
如图,连接交于点,连接,若,,,直接写出的长.
参考答案与试题解析
一、 选择题
1.
【答案】
A
2.
【答案】
B
3.
【答案】
D
4.
【答案】
B
5.
【答案】
D
6.
【答案】
C
7.
【答案】
C
二、 填空题
8.
【答案】
9.
【答案】
10.
【答案】
11.
【答案】
(1)菱形,
证明:∵ ,,
∴ 四边形是平行四边形.
∵
∴
又∵
∴
∴
∴ □是菱形;
(2),
理由如下:∵ 四边形是菱形,,
∴ 四边形是正方形.
12.
【答案】
有一组邻边相等的矩形是正方形
三、 解答题
13.
【答案】
证明:∵ ,
,
∵ ,
∴ ,
∴ ,
∴ ,,
∴ 四边形是菱形.
∴ ,,
∴ ,
∴ ,
∵ 四边形是菱形,,
∴ 四边形是正方形.
解:直线经过正方形的中心,理由如下:
连接交于点.
∵ 四边形是正方形.
∴ ,
∴ ,
∵ ,,,
∴ ,
∴ ,即点为的中点.
∴ 直线经过正方形的中心.
14.
【答案】
证明:过点作于,于,如图,
∵ 四边形为正方形,
.
,,
,.
∵ ,,
∴ .
在和中,
∴ ,
∴ ,
∴ 矩形是正方形.
解:如图,
在中,,
∵ ,
∴ ,
∴ 点与重合,此时是等腰直角三角形,
.
解:当时,
,
∵ ,
∴ .
∵ ,
∴ ,
15.
【答案】
如图所示:平行四边形即为所求;
如图所示:正方形即为所求.
16.
【答案】
证明:∵ 四边形是正方形,
∴ ,,
,
在和中,
∴ ,
∴ .
解:点在的中点时,四边形是正方形.
理由如下:
由折叠的性质得:,
,,
∵ ,是的中点,
∴ ,
∵ ,
∴ ,
∴ 四边形是菱形,是正方形对角线的交点,
∴ ,
∴ ,
∴ 四边形是正方形.
17.
【答案】
证明:∵ 四边形与四边形是平行四边形,
∴ ,
∴ ,,
∴ .
证明:延长,交于点.
∵ 四边形是平行四边形,
∴ ,
∵ 是中点,
∴ .
∵ ,,
∴ 四边形是平行四边形,
∴ ,
∴ ,
∴ .
∵ ,
∴ ,,
∴ .
在中,,
即,
∴ ,
∴ ,
∵ 四边形是平行四边形,
∴ 平行四边形是矩形.
解:,理由如下:
连接,设,
∵ ,,
四边形为平行四边形,
∴ 平行四边形是正方形,
∴ ,, ,
在和中,
,
,
∵ 四边形是矩形,
∴ ,,
由得,在平行四边中,
,.
,
∴ ,
在中,,
∴ ,
∴ .
18.
【答案】
证明:,,
四边形是平行四边形.
,.
,.
平分,,
,,
四边形是菱形.
证明:由知四边形是菱形,
,.
,
,
四边形是平行四边形,
.
,
.
,
.
,
,
,
.
解:,
四边形是矩形,
,
,
菱形是正方形,
.
,
,
,
.
同理,,则.
如图,过点作于点,
则,
,
.试卷第4页,总9页
试卷第5页,总9页
