2021—2022学年人教版数学八年级下册18.2.3正方形的性质 巩固提升练习(word版 含答案)
文档属性
| 名称 | 2021—2022学年人教版数学八年级下册18.2.3正方形的性质 巩固提升练习(word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 320.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 09:34:26 | ||
图片预览


文档简介
18.2.3 正方形的性质巩固提升练习
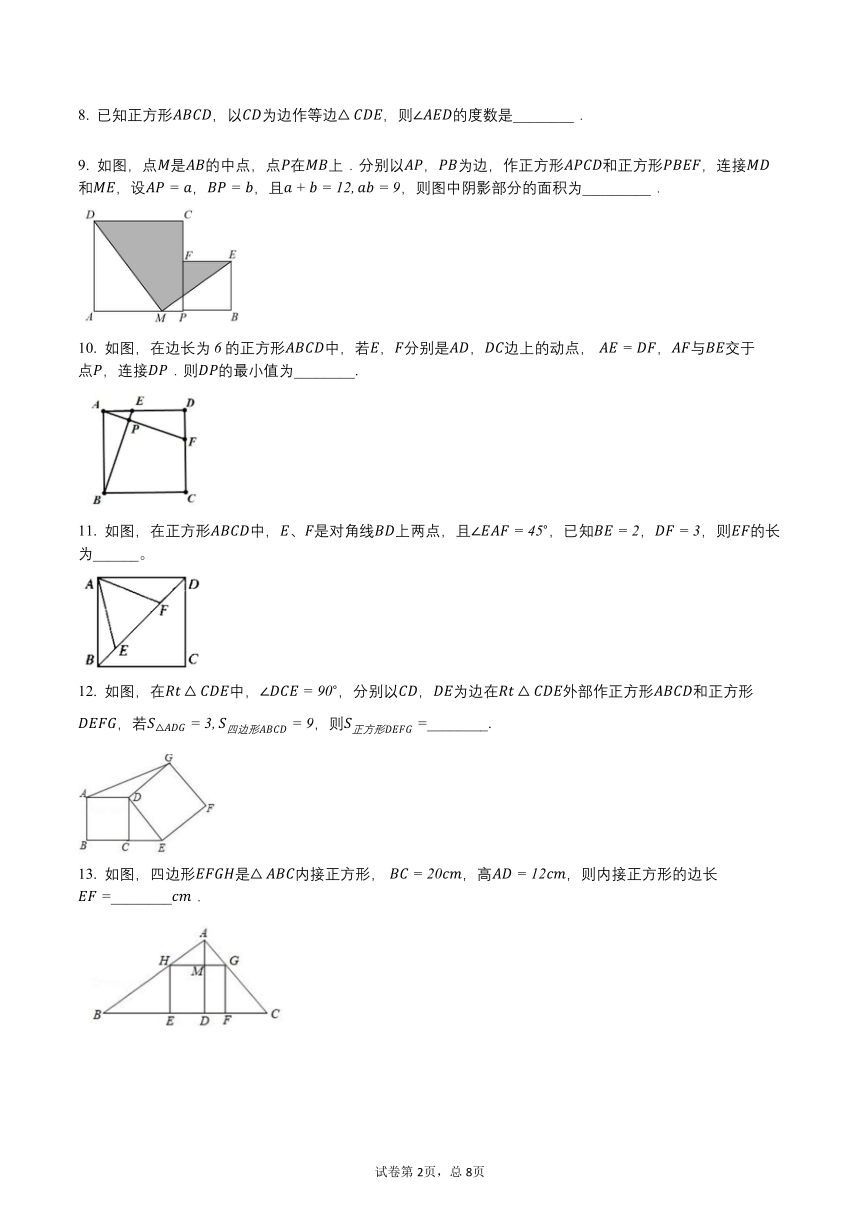
1. 如图,四边形是正方形,它的四个顶点都在坐标轴上,且正方形边长为,则点的坐标为( )
A. B. C. D.
2. 我们知道四边形具有不稳定性.如图,在平面直角坐标系中,边长为的正方形的边在轴上,的中点是坐标原点,固定点、,把正方形沿箭头方向推,使点落在轴正半轴上点处,则点的对应点的坐标为( )
A. B. C. D.
3. 如图,中,,若,则正方形和正方形的面积之和为 )
A. B. C. D.无法计算
4. 如图所示,四边形是正方形,边长为,点、分别在轴、轴的正半轴上,点在上,且点的坐标为,是上一动点,则的最小值为( )
A. B. C. D.
5. 如图,为正方形内一动点,,为的中点,则的最小值为()
A. B. C. D.
6. 如图,正方形的对角线是菱形的一边,菱形的对角线交正方形的一边于点,的度数是( )
A. B. C. D.
7. 如图,正方形的边长为,点在对角线上,且,,垂足为,则的长为( )
A. B. C. D.
8. 已知正方形,以为边作等边,则的度数是________.
9. 如图,点是的中点,点在上.分别以,为边,作正方形和正方形,连接和,设,,且,则图中阴影部分的面积为_________.
10. 如图,在边长为的正方形中,若,分别是,边上的动点, ,与交于点,连接.则的最小值为________.
11. 如图,在正方形中,、是对角线上两点,且,已知,,则的长为______。
12. 如图,在中,,分别以,为边在外部作正方形和正方形,若,则________.
13. 如图,四边形是内接正方形, ,高,则内接正方形的边长________.
14. 如图,正方形的边长为,为对角线,平分,求的长.
15. 如图,射线线段,为射线上一点,以为边作正方形,且点、与点在两侧,在线段上取一点,使,直线与线段,分别相交于点、(点与点、不重合).
求证:;
判断与的位置关系,并说明理由.
16. 如图,四边形是正方形,是边上的一点,是边的中点,平分.
(1)求证:=;
(2)若=,求的长.
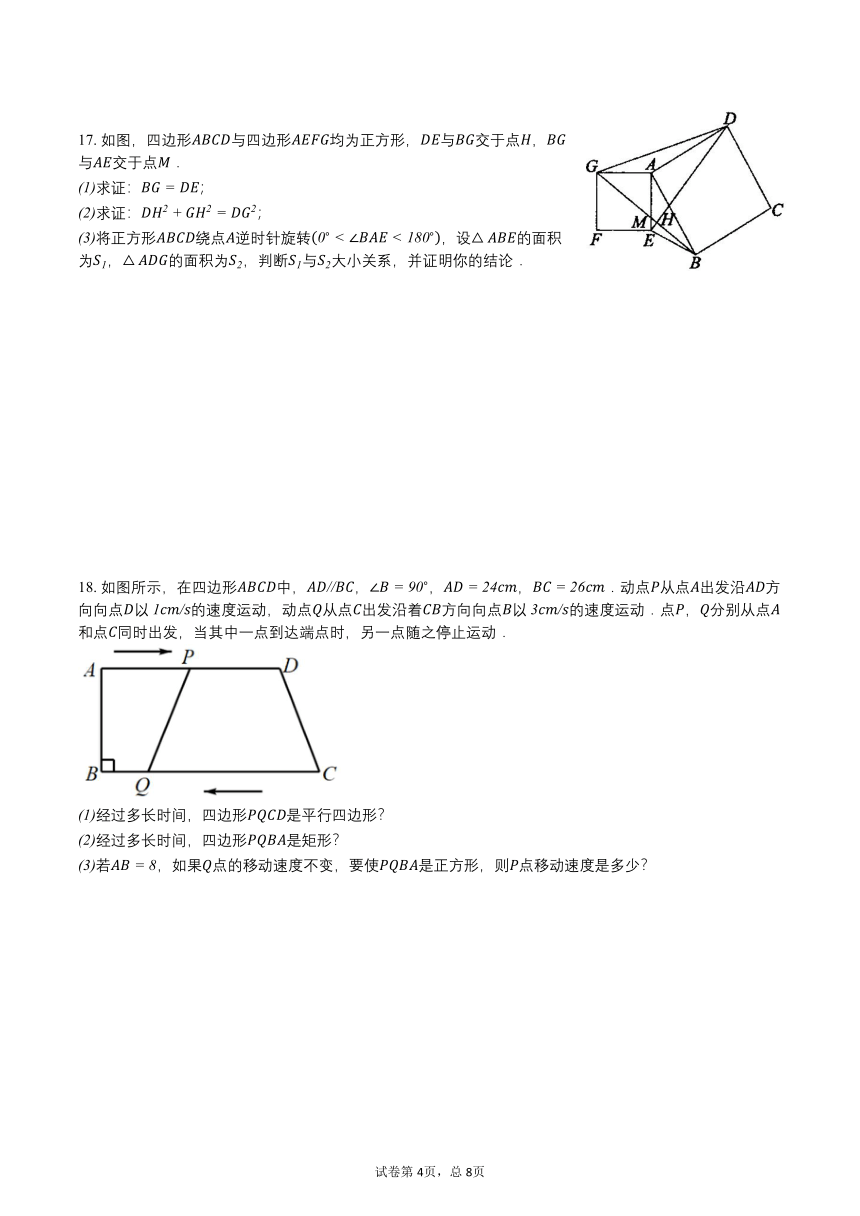
17. 如图,四边形与四边形均为正方形,与交于点,与交于点.
求证:;
求证:;
将正方形绕点逆时针旋转,设的面积为,的面积为,判断与大小关系,并证明你的结论.
18. 如图所示,在四边形中,,,,.动点从点出发沿方向向点以的速度运动,动点从点出发沿着方向向点以的速度运动.点,分别从点和点同时出发,当其中一点到达端点时,另一点随之停止运动.
经过多长时间,四边形是平行四边形?
经过多长时间,四边形是矩形?
若,如果点的移动速度不变,要使是正方形,则点移动速度是多少?
参考答案与试题解析
一、 选择题
1.
【答案】
C
2.
【答案】
D
3.
【答案】
C
4.
【答案】
B
5.
【答案】
D
6.
【答案】
C
7.
【答案】
A
二、 填空题
8.
【答案】
或
9.
【答案】
10.
【答案】
11.
【答案】
12.
【答案】
13.
【答案】
三、 解答题
14.
【答案】
解:在正方形中,
∴
又平分
∴ ,
∴ ).
∴ ,
又,
∴
15.
【答案】
证明:∵ 四边形为正方形,
∴ 平分,,
∴ ,
又,
∴ ;
解:,理由如下:
∵ ,
∴ .
∵ ,
∴ .
∵ ,,
∴ ,
∴ ,
∴ .
16.
【答案】
(1)证明:延长、交于点,如图所示.
四边形是正方形,
∴ ,
∴ .
平分,
,
,
.
在和中,
,
∴ ,
,
.
(2)解:∵ 四边形是正方形,
∴ .
设,则
,
,
∴ ,
解得:,
.
17.
【答案】
证明:∵ 四边形与四边形均为正方形,
∴ ,,,
∴ ,即,
∴ ,
∴ .
证明:由知,
∴ .
∵ ,,
∴ ,
∴ ,
∴ .
解:. 证明如下:
过点作交的延长线于,过点作交的延长线于.
∵ ,
∴ ,
,
∴ .
∵ ,,
∴ .
18.
【答案】
解:∵ ,
∴ 只要当时,四边形是平行四边形,
设运动时间为,,,
列式:,
解得,
∴ 经过秒,四边形是平行四边形.
∵ 且,
∴ 只要当时,四边形是矩形,
设运动时间为,,,
列式:,
解得,
∴ 经过秒,四边形是矩形.
当时,四边形是正方形,
设运动时间为,
列式:,
解得,
∵ ,
解得.试卷第4页,总9页
试卷第5页,总9页
1. 如图,四边形是正方形,它的四个顶点都在坐标轴上,且正方形边长为,则点的坐标为( )
A. B. C. D.
2. 我们知道四边形具有不稳定性.如图,在平面直角坐标系中,边长为的正方形的边在轴上,的中点是坐标原点,固定点、,把正方形沿箭头方向推,使点落在轴正半轴上点处,则点的对应点的坐标为( )
A. B. C. D.
3. 如图,中,,若,则正方形和正方形的面积之和为 )
A. B. C. D.无法计算
4. 如图所示,四边形是正方形,边长为,点、分别在轴、轴的正半轴上,点在上,且点的坐标为,是上一动点,则的最小值为( )
A. B. C. D.
5. 如图,为正方形内一动点,,为的中点,则的最小值为()
A. B. C. D.
6. 如图,正方形的对角线是菱形的一边,菱形的对角线交正方形的一边于点,的度数是( )
A. B. C. D.
7. 如图,正方形的边长为,点在对角线上,且,,垂足为,则的长为( )
A. B. C. D.
8. 已知正方形,以为边作等边,则的度数是________.
9. 如图,点是的中点,点在上.分别以,为边,作正方形和正方形,连接和,设,,且,则图中阴影部分的面积为_________.
10. 如图,在边长为的正方形中,若,分别是,边上的动点, ,与交于点,连接.则的最小值为________.
11. 如图,在正方形中,、是对角线上两点,且,已知,,则的长为______。
12. 如图,在中,,分别以,为边在外部作正方形和正方形,若,则________.
13. 如图,四边形是内接正方形, ,高,则内接正方形的边长________.
14. 如图,正方形的边长为,为对角线,平分,求的长.
15. 如图,射线线段,为射线上一点,以为边作正方形,且点、与点在两侧,在线段上取一点,使,直线与线段,分别相交于点、(点与点、不重合).
求证:;
判断与的位置关系,并说明理由.
16. 如图,四边形是正方形,是边上的一点,是边的中点,平分.
(1)求证:=;
(2)若=,求的长.
17. 如图,四边形与四边形均为正方形,与交于点,与交于点.
求证:;
求证:;
将正方形绕点逆时针旋转,设的面积为,的面积为,判断与大小关系,并证明你的结论.
18. 如图所示,在四边形中,,,,.动点从点出发沿方向向点以的速度运动,动点从点出发沿着方向向点以的速度运动.点,分别从点和点同时出发,当其中一点到达端点时,另一点随之停止运动.
经过多长时间,四边形是平行四边形?
经过多长时间,四边形是矩形?
若,如果点的移动速度不变,要使是正方形,则点移动速度是多少?
参考答案与试题解析
一、 选择题
1.
【答案】
C
2.
【答案】
D
3.
【答案】
C
4.
【答案】
B
5.
【答案】
D
6.
【答案】
C
7.
【答案】
A
二、 填空题
8.
【答案】
或
9.
【答案】
10.
【答案】
11.
【答案】
12.
【答案】
13.
【答案】
三、 解答题
14.
【答案】
解:在正方形中,
∴
又平分
∴ ,
∴ ).
∴ ,
又,
∴
15.
【答案】
证明:∵ 四边形为正方形,
∴ 平分,,
∴ ,
又,
∴ ;
解:,理由如下:
∵ ,
∴ .
∵ ,
∴ .
∵ ,,
∴ ,
∴ ,
∴ .
16.
【答案】
(1)证明:延长、交于点,如图所示.
四边形是正方形,
∴ ,
∴ .
平分,
,
,
.
在和中,
,
∴ ,
,
.
(2)解:∵ 四边形是正方形,
∴ .
设,则
,
,
∴ ,
解得:,
.
17.
【答案】
证明:∵ 四边形与四边形均为正方形,
∴ ,,,
∴ ,即,
∴ ,
∴ .
证明:由知,
∴ .
∵ ,,
∴ ,
∴ ,
∴ .
解:. 证明如下:
过点作交的延长线于,过点作交的延长线于.
∵ ,
∴ ,
,
∴ .
∵ ,,
∴ .
18.
【答案】
解:∵ ,
∴ 只要当时,四边形是平行四边形,
设运动时间为,,,
列式:,
解得,
∴ 经过秒,四边形是平行四边形.
∵ 且,
∴ 只要当时,四边形是矩形,
设运动时间为,,,
列式:,
解得,
∴ 经过秒,四边形是矩形.
当时,四边形是正方形,
设运动时间为,
列式:,
解得,
∵ ,
解得.试卷第4页,总9页
试卷第5页,总9页
