细节决定成败 规范赢得分数
图片预览




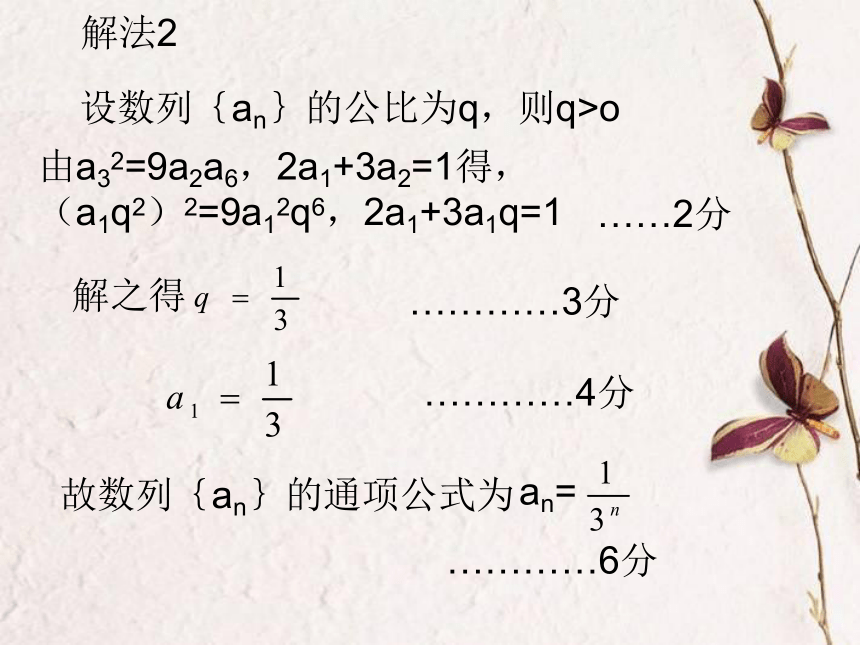

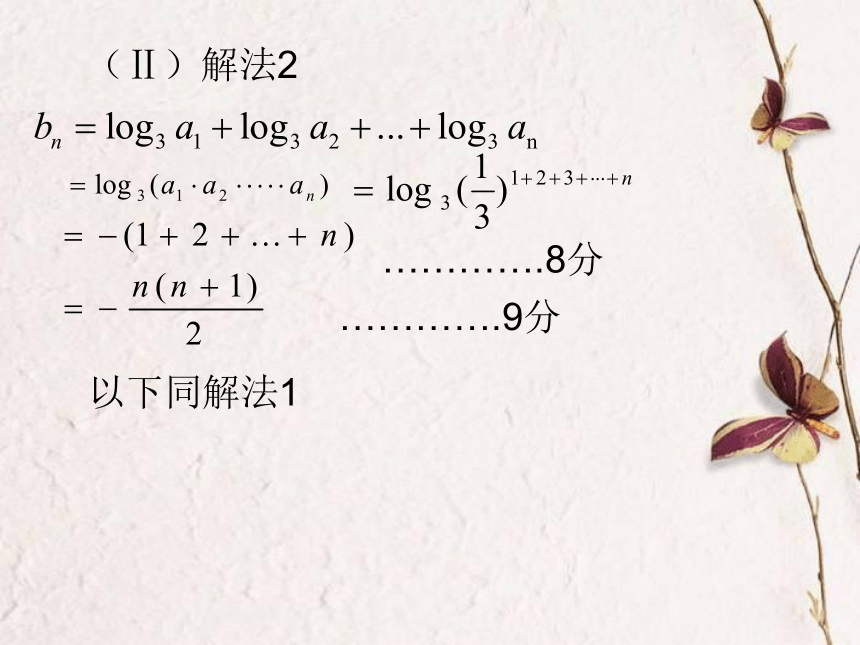


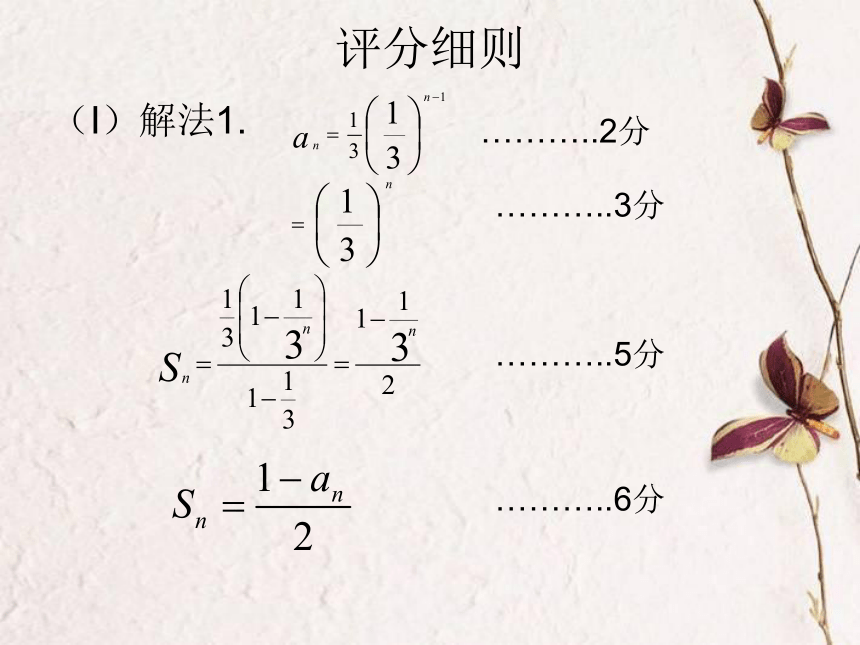
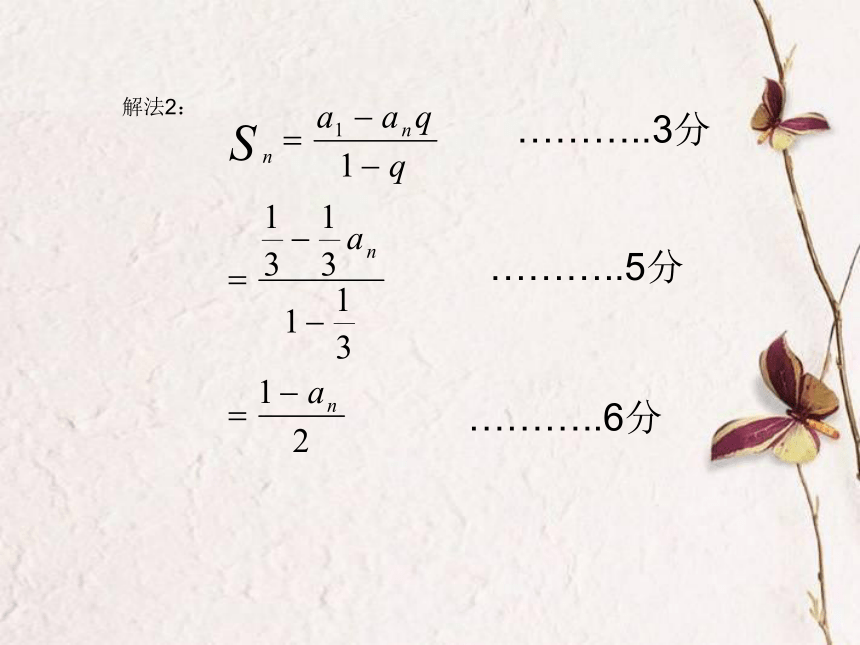
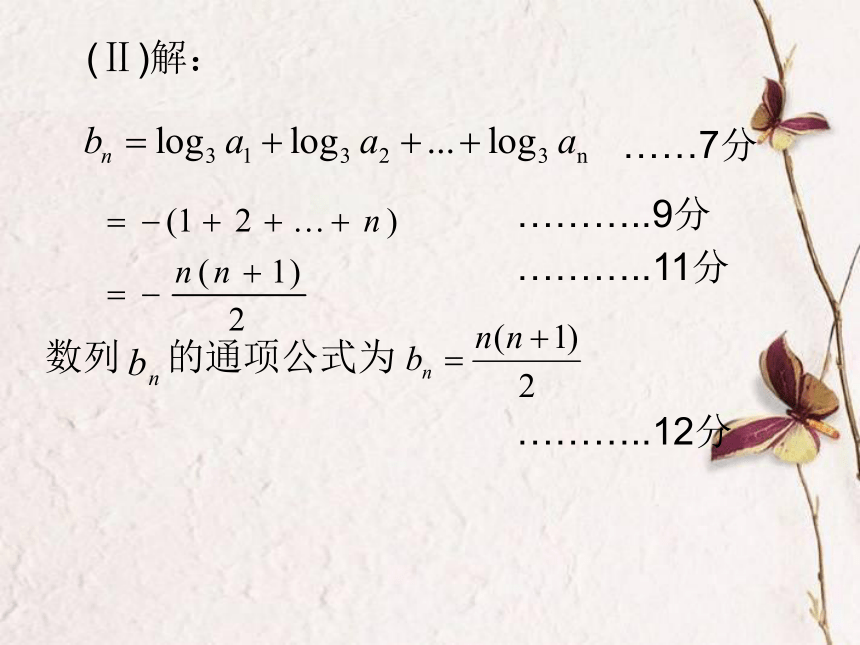
文档简介
课件103张PPT。细节决定成败 规范赢得分数 陈百华一、解读细则,走近试题 (理科17)(本小题满分12分,平均得分8.97)
(Ⅰ)解法1 ……………….6分解法2设数列{an}的公比为q,则q>o由a32=9a2a6,2a1+3a2=1得,
(a1q2)2=9a12q6,2a1+3a1q=1……2分解之得…………3分…………4分…………6分(Ⅱ)解法1………….8分………….9分………….10分…12分…11分(Ⅱ)解法2………….9分………….8分以下同解法1出现的错误:
1.没有注意到正项数列;
2.没有总结性语言;
3.通项公式即分数指数幂表示有误;
4.不会裂项相消法求和;
5.裂项相消的过程中哪些消掉,哪些留下来,不清楚;
6.对数计算出错;
7.等差数列前n项和不会求.(文科17)(本题满分12分,平均分5.99分)已知等比数列中,,公比(I)为的前项和,证明:(II)设求数列的通项公式。评分细则(I)解法1.………..2分………..3分………..5分………..6分解法2:………..3分………..5分………..6分(Ⅱ)解:……7分………..9分………..11分………..12分说明:
1.不计算出an,只证出给4分2.只写出公式写出其中两个和三个,给3分3.第二问中只验证n=1,2,3,给1分4.第二问中计算出每一步给1分5.没有指出通项公式的扣1分出现的错误1.没有指出数列的通项公式
2.等差数列求和公式不会
3.数列的通项公式和前n项和公式概念不清
4.对数计算不熟练
5.公式的初始形式没有呈现理科18(本题满分12分,平均分7.35) 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
(Ⅰ)证明:PA⊥BD;
(Ⅱ)若PD=AD,求二面角A-PB-C的余弦值.评分细则(Ⅰ)第一个3分段:能够利用余弦定理或正弦定理或平面几何的方法完整得出结论
AD⊥BD,给3分,有证明但过程不完整,给1分,没有证明过程就得出结论AD⊥BD,不给分.
第二个3分段:利用三垂线定理或线面垂直的判定与性质或向量法完整得出结论
PA⊥BD,给3分,若条件不完整,扣1分.(Ⅱ)解法1.坐标法
指出正确建系的方法步骤,给1分;
得到相应的点或向量的坐标,给1分;
求出面PAB的法向量的坐标,给1分;
求出面PBC的法向量的坐标,给1分;
求出两个法向量的夹角余弦值,给1分;
指出二面角的余弦值,给1分.
解法2:几何法
作出一个垂直,给1分;
证明另一个垂直,给1分;
指出二面角的平面角,给1分;
分别求出三角形三边长度,给1分;
计算出余弦值,给1分;
指出二面角的余弦值,给1分.解法3:向量法
在面PAB和面PBC内分别得到直线PB的两个法向量,每个1分;
指出法向量的夹角即为二面角的大小,给1分;
分别求出相应线段长,给1分;
计算出法向量的夹角的余弦值,给1分;
指出二面角的余弦值,给1分.说明:
1.没有指出正弦定理或余弦定理,有过程,不扣分;
2.指出余弦定理或正弦定理,没有过程,不扣分;
3.用三垂线定理时,没有说明射影,不扣分;
4.个别符号表示错误,不扣分,如把包含符号写成属于符号.出现的错误1. AD⊥BD证明步骤没有,直接得到结论;
2.误把分别在两个互相垂直平面内的两条直线互相垂直作为线线垂直的判定;
3.坐标运算出错,即法向量计算不正确;
4.法向量的夹角和二面角的平面角的关系不清;
5.夹角计算出错;
6.没有指出二面角的平面角.文科18(本题满分12分,平均分4.7)如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
(Ⅰ)证明:PA⊥BD;
(Ⅱ)设PD=AD=1,求棱锥D-PBC的高 .
评分细则(Ⅰ)同理科
(Ⅱ)解法1:几何法
作出高,给1分;证明高,给2分;计算出高,给2分;总结,给1分.
解法2:向量法
坐标系建立,给1分;得到相应坐标,给1分;求出法向量,给2分;代入高的向量坐标公式,求出高,给1分;总结,给1分.
解法3:等积法
写出等体积公式,给1分;转化成底面积与高之积,给1分;算出三角形BCD的面积,给1分;证出三角形PBC为直角三角形,给1分;计算出三角形PBC的面积给1分;求出高并指出棱锥的高,给1分.
说明:1.不出现高或不总结扣1分;
2.所有向量都没有箭头,扣2分,部分没有,扣1分;出现的错误:1.没有指出棱锥的高,或没有说明h就是棱锥的高2.AD⊥BD没有证明
3.PB⊥BC没有证明理科19(本题满分12分,平均分10.12) 某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品,现用两种新配方(分别称为A配方和B配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:(Ⅰ)分别估计用A配方,B配方生产的产品的优质品率;
(Ⅱ)已知用B配方生成的一件产品的利润y(单位:元)
与其质量指标值t的关系式为从用B配方生产的产品中任取一件,其利润记为X
(单位:元),求X的分布列及数学期望.(以试验
结果中质量指标值落入各组的频率作为一件产品的
质量指标值落入相应组的概率 )评分细则(Ⅰ)解法1:用A配方生产的产品中优质品的频率为
所以用A配方生产的产品的优质品率的估计值0.3
……………3分
用B配方生产的产品中优质品的频率为
所以用B配方生产的产品的优质品率的估计值为0.42
………………6分解法2:P(A配方生产的优质品)=P(B配方生产的优质品)=……………6分解法3:用A配方生产的优质品率P1=用B配方生产的优质品率P2=……………6分解法4:用A配方、B配方生产的优质品率分别为P1、P2,则P1=
P2=……………6分解法5:由试验结果知,A配方生产的100件产品
中优质品是为30件,所以A配方的优质频率为0.3,
同理可知B配方的优质品率为0.42.……………6分(Ⅱ)用B配方生产的100件产品中,其质量指标值落入
区间的频率分别为0.04,,054,0.42,因此X的可能值
为-2,2,4
P(X= -2)=0.04, P(X=2)=0.54, P(X=4)=0.42,……………3分X的数学期望值EX=-2×0.04+2×0.54+4×0.42=2.68……………6分说明:1.分数、小数、百分数无论哪种形式都可以;
2.没有文字说明,直接得到优质品率,
如PA= ,PB= ,扣2分;
3.有文字说明,但优质品率直接写出结果,没有过程,如用A配方生产的产品的优质品率P1=0.3,
用B配方生产的产品的优质品率P2=0.42,扣2分.4.分布列以表格形式或一一列出形式都可以,一个给1分;
5.数学期望公式正确,给2分,计算正确,给1分;
5.若分布列中概率计算有误,只要EX公式正确,给1分;
6.若求出P(t<94)=0.04,P(94≦t<102)=0.54,
P(t≧102)=0.42,没有转化成利润X的概率,
或转换出错,给2分.出现的错误1.没有文字说明;
2.没有计算过程;
3.优质品率和频率混淆;
4.数据计算出错,特别是数学期望;
文科19(本题满分12分,平均分8.97) 某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品,现用两种新配方(分别称为A配方和B配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:(Ⅰ)分别估计用A配方,B配方生产的产品的优质品率;
(Ⅱ)已知用B配方生成的一件产品的利润y(单位:元)
与其质量指标值t的关系式为 估计用B配方生产的一件产品的利润大于0的概率,
并求用B配方生产的上述100件产品平均一件的利润 . (Ⅱ)用B配方生产的一件产品的利润大于0的概率当且
仅当t≥94,由试验结果知,t≥94的频率为0.96, 所以用B配方生产的一件产品的利润大于0的概率估计
值为0.96. 用B配方生产的上述100件产品平均一件的利润为=2.68(元) (Ⅰ)同理科……………………..8分……………………..9分……………………..12分评分细则:说明:1.没有指出频率,直接求出概率的扣1分;
2.求出频率,没有指出是概率的扣1分;
3.平均一件的利润,公式2分,结果1分;
4.不带单位,不扣分;
5.第一问与理科一样.
理科20(本题满分12分,平均分4.66) 在平面直角坐标系xOy中,已知点A(0,-1),B点在
直线y = -3上,M点满足 M点的轨迹为曲线C. (Ⅰ)求C的方程; (Ⅱ)P为C上的动点,l为C在P点处得切线,求O点
到l距离的最小值.评分细则(Ⅰ)解法1:设M(x,y),由已知B(x,-3),A(0,-1)(-x,-1-y),(0,-3-y),(x,-2)因为,所以∴(-x,-4-2y) ·(x,-2)=0∴曲线C的方程为…………..2分…………..4分…………..5分(Ⅰ)解法2:设M(x,y),由已知B(x,-3),A(0,-1)设AB中点为N,则N(0.5x,-2)…………..2分因为,所以,∴∴(-x,-4-2y) ·(x,-2)=0∴曲线C的方程为…………..4分…………..5分(Ⅰ)解法3:同解法2,得到∴MN是线段AB的垂直平分线∴∴∴曲线C的方程为…………..5分…………..4分(Ⅰ)解法3:同解法2,得到即M点的轨迹是以点A为焦点,以y=-3为准线的抛物线∴曲线C的方程为…………..5分…………..4分(Ⅱ)解法1:设P(x0,y0)为曲线C:y/=0.5x,所以切线的斜率k=0.5x0∴切线方程即则点O到切线的距离又所以 当x0=0时取等号,所以O点到l距离的最小值2. …………..7分…………..8分…………..10分…………..11分…………..12分解法2:同解法1得到由判别式法得到d≥2,当d=2时代入方程得x0=0所以x0=0时,O点到l距离的最小值2. …………..10分…………..11分…………..12分解法3:设切线方程y=kx+b,代入得x2-4kx-4b-8=0,△=k2+b+2=0则点O到切线的距离当k=0时取等号,所以O点到l距离的最小值2. ………8分….9分…………..12分….11分说明:出现的错误:1.没有指出等号成立的条件;4.最小值不会求;2.点到直线距离公式不会;3.不会求切线方程;6.没有向量的坐标.文科20(本题满分12分,平均分2.59)在平面直角坐标系xOy中,曲线 与坐标轴的交点都在圆C上(Ⅰ)求圆C的方程;(Ⅱ)若圆C与直线交与A,B两点,且,求a的值. 评分细则解:求出曲线与坐标轴的三个交点………… 2分(Ⅰ)解法1:设圆心坐标求出圆心坐标求出圆心半径写出圆的方程………… 3分………… 4分………… 5分………… 6分解法2:设圆的标准方程代入三个点的坐标,得到三个方程组成的方程组解出方程组的解写出圆的方程………… 6分………… 3分………… 4分………… 5分解法3:设圆的一般方程代入三个点的坐标,得到三个方程组成的方程组解出方程组的解写出圆的方程………… 6分………… 3分………… 4分………… 5分解法4:分别求出两个中垂线方程求出中垂线的交点坐标,得到圆心坐标求出圆心半径写出圆的方程………… 5分………… 6分………… 3分………… 4分(Ⅱ)联立圆的方程和直线方程组成的方程组消去未知数y,得到关于x的一元二次方程….7分….8分解法1:利用韦达定理,得到方程的两根和与积….9分….10分韦达定理代入上式,求出a代入△>0,验证….11分….12分解法2:求出一元二次方程的根,得到A,B坐标….9分….10分把A,B坐标代入上式,求出a验证….11分….12分解法3:求出弦长AB设AB的中点G,求出G点坐标,计算OG的长根据AB=2OG,求出a代入检验…………………..9分…………………..10分…………………..11分…………………..12分说明1.三个交点坐标若有一个对,而没有全对,给1分;
2.设圆的方程为其它非常规形式,若能解题,给分;
3.若没有圆心、半径的求解过程,扣2分;
4.若求出a=-1,又解出△>0,不扣分;
5.若第一问圆的方程有错,而第二问过程及数据没有新的错误,第二问给分不超过3分.出现的错误:4.没有对a=-1进行验证;不会处理;1.一元二次方程化简错误;3.解圆的方程组出错;2.理科21(本题满分12分,平均分4.24)已知函数 处的切线方程为 (Ⅰ)求 a,b的值;(Ⅱ)如果当 x>0,且x≠1时,求k的取值范围.评分细则(Ⅰ)解法1:…2分,且过点 (1,1),故 所以解得: b=1a=1…………3分…………4分…………5分…………6分(Ⅰ)解法2:………..2分所以又f(1)=b故曲线y=f(x)在(1,f(1))处的切线方程为与已知切线方程x+2y-3=0相比较,可得a=1,b=1………..3分………..4分………..6分(Ⅱ)解法1:由(Ⅰ)知 考虑函数 …….7分…….8分,h(x)递减 故当0h(1)=0,可得当x>1时,h(x)0,且x≠1时,即………..9分(x)>0, ,h(x) >h(1)=0,可得:h(x)<0,这与题设矛盾(iii)设k≥1时,此时 (x)>0, h(x)是增函数当x>1时,h(x) >h(1)=0,可得:h(x)<0,这与题设矛盾………..10分………..11分………..12分综上可得,k的取值范围是(Ⅱ)解法2:由(Ⅰ)知 所以,得令令则令则为单调增函数………..7分………..8分………..9分当01时,u(t)>u(1)=0,即g(x)>0,于是h/(x)>0所以,h(x)在单调递增又所以k的取值范围是………..10分………..11分………..12分(Ⅱ)解法3:由(Ⅰ)知 所以,得………..7分………..8分令g(x)=x2lnx+lnx-x2+1则当01时,单调递增,所以g(x)在(0,1)单调递增,g(x)g(1)=0即h(x)在(0,1)单调递减即h(x)在单调递增又所以k的取值范围是………..11分………..12分………..10分出现的错误:1.不会求导数;
2.不理解切线的含义;
3.不能发现f(1)=1;
4.解方程组出错;
5.不会分离参数;
6.分离后的函数的单调性不会证明;
7.证明单调性不严密.文科21(本题满分12分,平均分2.06)已知函数 处的切线方程为 (Ⅰ)求 a,b的值;(Ⅱ)证明:当 x>0,且x≠1时,评分细则(Ⅰ)同理科(Ⅱ)解法1:由(Ⅰ)知 …….8分………..7分考虑函数所以当x≠1时,故当0h(1)=0,可得当x>1时,h(x)0,且x≠1时,即…….12分…10分…….11分(Ⅱ)解法2:令h(x)=x2-2xlnx-1,则h/(x)=2(x-lnx-1),h//(x)=2(1-1/x)当0h/(1)=0,
h(x)单调递增,h(x)1时,h//(x)>0,h/(x)单调递增,h/(x)>h/(1)=0,
h(x)单调递增,h(x)>h(1)=0,从而当 x>0,且x≠1时,…….12分…….7分…….8分…….10分…….11分出现的错误:1.不会求导数;
2.不理解切线的含义;
3.不能发现f(1)=1;
4.解方程组出错;
5.不会作差;
6.作差后的函数的单调性不会证明.文理科22(本题满分10分,理科平均4.31分,文科平均2.14分) D,E分别为 △ABC的边 AB,AC上的点,且不与
△ABC的顶点重合.已知 AE的长为 m,AC的长为n,
AD,AB的长是关于 x的方程 x2-14x+mn=0的两个根 .(Ⅰ)证明:C,B,D,E四点共圆; (Ⅱ)若 ∠A=900,且 m=4,n=6,
求C,B,D,E所在圆的半径. 评分细则:(I)连接DE,根据题意在△ADE和△ACB中, 即……2分又∠DAE=∠CAB,从而△ADE∽△ACB
因此∠ADE=∠ACB,所以C,B,D,E四点共圆。……3分……5分(Ⅱ)解法1:m=4, n=6时,方程x2-14x+mn=0的两根
为x1=2,x2=12.故 AD=2,AB=12.……6分 取CE的中点G,DB的中点F,分别过G,F作AC,AB的
垂线,两垂线相交于H点,连接DH.因为C,B,D,E
四点共圆,所以C,B,D,E四点所在圆的圆心为H,
半径为DH. 由于∠A=900,故GH∥AB, HF∥AC. HF=AG=5,DF= 5. 故C,B,D,E四点所在圆的半径为5 ……7分……9分……10分解法2:求出AD=2,AB=12,EB=4,ED=2sin∠EDB=sin∠EDA=设C,B,D,E所在圆的半径为R,则 故C,B,D,E四点所在圆的半径为5 ……9分……10分……7分……6分解法3:以A为原点,AB所在直线为x轴,AC所在直
线为y轴建立平面直角坐标系.线段BC的中垂线方程:2x-y-9=0线段DE的中垂线方程:x-2y+3=0解方程组得x=7,y=5,所以圆心坐标为(7,5)故圆的半径为……9分……10分……7分……6分……8分解法3:以A为原点,AB所在直线为x轴,AC所在直
线为y轴建立平面直角坐标系.
则D(2,0),B(12,0),E(0,4),C(0,6)设C,B,D,E所在圆的方程为x2+y2+dx+ey+f=0将D,B,E三点的坐标代入上式,
解方程组得:d=-14,e=-10,f=24所以x2+y2-14x-10y+24=0所求半径R=……9分……10分……7分……6分说明:
1.只要有∠ADE=∠ACB,C,B,D,E四点共圆,给1分
2.正弦定理写对,给1分出现的错误:
1.三角形相似没有指出公共角;
2.切割线定理逆定理不能作为四点共圆的证明方法;
3.解方程组出现错误;
4.不会利用根与系数的关系.23 理科(本题满分12分,平均分7.27分)设函数f(x)=|x-a|+3x,其中a>0(Ⅰ)当 a=1时,求不等式f(x) ≥3x+2的解集;(Ⅱ)若不等式 f(x) ≤0的解集为{x|x≤-1},求a的值.评分细则:(Ⅰ)a=1时,不等式f(x) ≥3x+2可化为|x-1|≥2 …2分法1:由此得x-1≥2或x-1≤-2法2:两边平方得x2-2x+1≥4法3:分段讨论得{x≥1x-1≥2或{X<1x-1≤2所以x≥3或x≤-1∴不等式f(x) ≥3x+2的解集是{x|x≥3或x≤-1}…………….4分…………….5分(Ⅱ)由f(x) ≤0得: |x-a|+3x ≤0法1:此不等式可化为所以∵a>0,∴原不等式的解集为{x|x≤-a/2}由题设得-a/2=-1,∴a=2….7分….8分….9分….10分法2:此不等式可化为3x≤x-a≤-3x所以,x≤0,x≤a/4,x≤-a/2∵a>0,∴原不等式的解集为{x|x≤-a/2}….9分由题设得-a/2=-1,∴a=2….10分….8分法3:由|x-a|+3x ≤0得|x-a| ≤-3x,可化为∵a>0,∴原不等式的解集为{x|x≤-a/2}….9分由题设得-a/2=-1,∴a=2….10分….7分法4:由f(x) ≤0的解集为{x|x≤-1}所以x=-1是方程f(x) =0的根,代入得|a+1|=3∵a>0,∴a=2把a=2代入f(x) ≤0得: |x-2|+3x ≤0解此不等式得3x≤x-2≤3x,x≤-1∴当a=2时不等式 f(x) ≤0的解集为{x|x≤-1}….7分….10分说明1.不等式结果可以写成2.不写并集不给分,集合表达式不正确,不给分出现的错误:
1.不会解绝对值不等式;
2.解集形式表示有误;
3.不会分类讨论;
4.不会去掉绝对值符号.
5.不总结.㈠了解高考评分细则对教学的指导意义 ㈡制定评分细则的基本原则㈢阅卷评分的基本要求二、分析细则,感受试题1.符号图形配文字
2.呈现公式要原始
3.试题总结要牢记
4.结论证明要严密
5.简单试题写详细
6.运算结果要彻底
7.字母引入有明细
8.试题容易莫大意
9.书写规范有条理
10.将错就错没关系8分4分文科缺少过程或必要的文字说明12分4分
没有呈现等比数列的前n项
和公式的原始形式12分11分没有指出数列的前n项和即没有对Tn交代.11分
总结出错,
或没有总结没有指出棱锥的高,
或没有说明h就是
棱锥的高11分4分没有写解集9分 AD⊥BD没有证明9分AD⊥BD没有证明7分AD⊥BD没有证明,
高没有证明8分切割线定理逆定理不能作为四点共圆的证明方法10分3分 没有向量的坐标10分优质品率的计算没有过程12分12分12分12分10分10分三、规范指导,赢得试题1.重视过程完整,把握推理的严谨性
2.抓好“三基”,侧重通性通法的落实
3.书写讲究整洁,表达要有条理
4. 统筹兼顾全局,合理支配时间共轭复数打头阵,函数性质领风骚;
定义变换与对称,奇偶周期和单调;
向量三角相结合,三角公式得记牢;
框图积分三视图,新增内容头一招;
线性规划二项式,中规中矩老一套;
数列概率换模样,学生欢喜得分高;
定义性质离心率,解析几何难不倒;
轨迹切线最小值,平时训练已预料;
立体几何向量求,球体棱锥年年考。
导数压轴真给力,分类讨论弄技巧;
平面几何不等式,认真审题要选好;
不等容易几何难,忘涂题号无紧要;
今年试题显平和,师生普遍反应好;
认真分析高考题,来年命中不得了。年年岁岁题相似,岁岁年年卷不同——2012年河南省高考数学试题特点
(Ⅰ)解法1 ……………….6分解法2设数列{an}的公比为q,则q>o由a32=9a2a6,2a1+3a2=1得,
(a1q2)2=9a12q6,2a1+3a1q=1……2分解之得…………3分…………4分…………6分(Ⅱ)解法1………….8分………….9分………….10分…12分…11分(Ⅱ)解法2………….9分………….8分以下同解法1出现的错误:
1.没有注意到正项数列;
2.没有总结性语言;
3.通项公式即分数指数幂表示有误;
4.不会裂项相消法求和;
5.裂项相消的过程中哪些消掉,哪些留下来,不清楚;
6.对数计算出错;
7.等差数列前n项和不会求.(文科17)(本题满分12分,平均分5.99分)已知等比数列中,,公比(I)为的前项和,证明:(II)设求数列的通项公式。评分细则(I)解法1.………..2分………..3分………..5分………..6分解法2:………..3分………..5分………..6分(Ⅱ)解:……7分………..9分………..11分………..12分说明:
1.不计算出an,只证出给4分2.只写出公式写出其中两个和三个,给3分3.第二问中只验证n=1,2,3,给1分4.第二问中计算出每一步给1分5.没有指出通项公式的扣1分出现的错误1.没有指出数列的通项公式
2.等差数列求和公式不会
3.数列的通项公式和前n项和公式概念不清
4.对数计算不熟练
5.公式的初始形式没有呈现理科18(本题满分12分,平均分7.35) 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
(Ⅰ)证明:PA⊥BD;
(Ⅱ)若PD=AD,求二面角A-PB-C的余弦值.评分细则(Ⅰ)第一个3分段:能够利用余弦定理或正弦定理或平面几何的方法完整得出结论
AD⊥BD,给3分,有证明但过程不完整,给1分,没有证明过程就得出结论AD⊥BD,不给分.
第二个3分段:利用三垂线定理或线面垂直的判定与性质或向量法完整得出结论
PA⊥BD,给3分,若条件不完整,扣1分.(Ⅱ)解法1.坐标法
指出正确建系的方法步骤,给1分;
得到相应的点或向量的坐标,给1分;
求出面PAB的法向量的坐标,给1分;
求出面PBC的法向量的坐标,给1分;
求出两个法向量的夹角余弦值,给1分;
指出二面角的余弦值,给1分.
解法2:几何法
作出一个垂直,给1分;
证明另一个垂直,给1分;
指出二面角的平面角,给1分;
分别求出三角形三边长度,给1分;
计算出余弦值,给1分;
指出二面角的余弦值,给1分.解法3:向量法
在面PAB和面PBC内分别得到直线PB的两个法向量,每个1分;
指出法向量的夹角即为二面角的大小,给1分;
分别求出相应线段长,给1分;
计算出法向量的夹角的余弦值,给1分;
指出二面角的余弦值,给1分.说明:
1.没有指出正弦定理或余弦定理,有过程,不扣分;
2.指出余弦定理或正弦定理,没有过程,不扣分;
3.用三垂线定理时,没有说明射影,不扣分;
4.个别符号表示错误,不扣分,如把包含符号写成属于符号.出现的错误1. AD⊥BD证明步骤没有,直接得到结论;
2.误把分别在两个互相垂直平面内的两条直线互相垂直作为线线垂直的判定;
3.坐标运算出错,即法向量计算不正确;
4.法向量的夹角和二面角的平面角的关系不清;
5.夹角计算出错;
6.没有指出二面角的平面角.文科18(本题满分12分,平均分4.7)如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
(Ⅰ)证明:PA⊥BD;
(Ⅱ)设PD=AD=1,求棱锥D-PBC的高 .
评分细则(Ⅰ)同理科
(Ⅱ)解法1:几何法
作出高,给1分;证明高,给2分;计算出高,给2分;总结,给1分.
解法2:向量法
坐标系建立,给1分;得到相应坐标,给1分;求出法向量,给2分;代入高的向量坐标公式,求出高,给1分;总结,给1分.
解法3:等积法
写出等体积公式,给1分;转化成底面积与高之积,给1分;算出三角形BCD的面积,给1分;证出三角形PBC为直角三角形,给1分;计算出三角形PBC的面积给1分;求出高并指出棱锥的高,给1分.
说明:1.不出现高或不总结扣1分;
2.所有向量都没有箭头,扣2分,部分没有,扣1分;出现的错误:1.没有指出棱锥的高,或没有说明h就是棱锥的高2.AD⊥BD没有证明
3.PB⊥BC没有证明理科19(本题满分12分,平均分10.12) 某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品,现用两种新配方(分别称为A配方和B配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:(Ⅰ)分别估计用A配方,B配方生产的产品的优质品率;
(Ⅱ)已知用B配方生成的一件产品的利润y(单位:元)
与其质量指标值t的关系式为从用B配方生产的产品中任取一件,其利润记为X
(单位:元),求X的分布列及数学期望.(以试验
结果中质量指标值落入各组的频率作为一件产品的
质量指标值落入相应组的概率 )评分细则(Ⅰ)解法1:用A配方生产的产品中优质品的频率为
所以用A配方生产的产品的优质品率的估计值0.3
……………3分
用B配方生产的产品中优质品的频率为
所以用B配方生产的产品的优质品率的估计值为0.42
………………6分解法2:P(A配方生产的优质品)=P(B配方生产的优质品)=……………6分解法3:用A配方生产的优质品率P1=用B配方生产的优质品率P2=……………6分解法4:用A配方、B配方生产的优质品率分别为P1、P2,则P1=
P2=……………6分解法5:由试验结果知,A配方生产的100件产品
中优质品是为30件,所以A配方的优质频率为0.3,
同理可知B配方的优质品率为0.42.……………6分(Ⅱ)用B配方生产的100件产品中,其质量指标值落入
区间的频率分别为0.04,,054,0.42,因此X的可能值
为-2,2,4
P(X= -2)=0.04, P(X=2)=0.54, P(X=4)=0.42,……………3分X的数学期望值EX=-2×0.04+2×0.54+4×0.42=2.68……………6分说明:1.分数、小数、百分数无论哪种形式都可以;
2.没有文字说明,直接得到优质品率,
如PA= ,PB= ,扣2分;
3.有文字说明,但优质品率直接写出结果,没有过程,如用A配方生产的产品的优质品率P1=0.3,
用B配方生产的产品的优质品率P2=0.42,扣2分.4.分布列以表格形式或一一列出形式都可以,一个给1分;
5.数学期望公式正确,给2分,计算正确,给1分;
5.若分布列中概率计算有误,只要EX公式正确,给1分;
6.若求出P(t<94)=0.04,P(94≦t<102)=0.54,
P(t≧102)=0.42,没有转化成利润X的概率,
或转换出错,给2分.出现的错误1.没有文字说明;
2.没有计算过程;
3.优质品率和频率混淆;
4.数据计算出错,特别是数学期望;
文科19(本题满分12分,平均分8.97) 某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品,现用两种新配方(分别称为A配方和B配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:(Ⅰ)分别估计用A配方,B配方生产的产品的优质品率;
(Ⅱ)已知用B配方生成的一件产品的利润y(单位:元)
与其质量指标值t的关系式为 估计用B配方生产的一件产品的利润大于0的概率,
并求用B配方生产的上述100件产品平均一件的利润 . (Ⅱ)用B配方生产的一件产品的利润大于0的概率当且
仅当t≥94,由试验结果知,t≥94的频率为0.96, 所以用B配方生产的一件产品的利润大于0的概率估计
值为0.96. 用B配方生产的上述100件产品平均一件的利润为=2.68(元) (Ⅰ)同理科……………………..8分……………………..9分……………………..12分评分细则:说明:1.没有指出频率,直接求出概率的扣1分;
2.求出频率,没有指出是概率的扣1分;
3.平均一件的利润,公式2分,结果1分;
4.不带单位,不扣分;
5.第一问与理科一样.
理科20(本题满分12分,平均分4.66) 在平面直角坐标系xOy中,已知点A(0,-1),B点在
直线y = -3上,M点满足 M点的轨迹为曲线C. (Ⅰ)求C的方程; (Ⅱ)P为C上的动点,l为C在P点处得切线,求O点
到l距离的最小值.评分细则(Ⅰ)解法1:设M(x,y),由已知B(x,-3),A(0,-1)(-x,-1-y),(0,-3-y),(x,-2)因为,所以∴(-x,-4-2y) ·(x,-2)=0∴曲线C的方程为…………..2分…………..4分…………..5分(Ⅰ)解法2:设M(x,y),由已知B(x,-3),A(0,-1)设AB中点为N,则N(0.5x,-2)…………..2分因为,所以,∴∴(-x,-4-2y) ·(x,-2)=0∴曲线C的方程为…………..4分…………..5分(Ⅰ)解法3:同解法2,得到∴MN是线段AB的垂直平分线∴∴∴曲线C的方程为…………..5分…………..4分(Ⅰ)解法3:同解法2,得到即M点的轨迹是以点A为焦点,以y=-3为准线的抛物线∴曲线C的方程为…………..5分…………..4分(Ⅱ)解法1:设P(x0,y0)为曲线C:y/=0.5x,所以切线的斜率k=0.5x0∴切线方程即则点O到切线的距离又所以 当x0=0时取等号,所以O点到l距离的最小值2. …………..7分…………..8分…………..10分…………..11分…………..12分解法2:同解法1得到由判别式法得到d≥2,当d=2时代入方程得x0=0所以x0=0时,O点到l距离的最小值2. …………..10分…………..11分…………..12分解法3:设切线方程y=kx+b,代入得x2-4kx-4b-8=0,△=k2+b+2=0则点O到切线的距离当k=0时取等号,所以O点到l距离的最小值2. ………8分….9分…………..12分….11分说明:出现的错误:1.没有指出等号成立的条件;4.最小值不会求;2.点到直线距离公式不会;3.不会求切线方程;6.没有向量的坐标.文科20(本题满分12分,平均分2.59)在平面直角坐标系xOy中,曲线 与坐标轴的交点都在圆C上(Ⅰ)求圆C的方程;(Ⅱ)若圆C与直线交与A,B两点,且,求a的值. 评分细则解:求出曲线与坐标轴的三个交点………… 2分(Ⅰ)解法1:设圆心坐标求出圆心坐标求出圆心半径写出圆的方程………… 3分………… 4分………… 5分………… 6分解法2:设圆的标准方程代入三个点的坐标,得到三个方程组成的方程组解出方程组的解写出圆的方程………… 6分………… 3分………… 4分………… 5分解法3:设圆的一般方程代入三个点的坐标,得到三个方程组成的方程组解出方程组的解写出圆的方程………… 6分………… 3分………… 4分………… 5分解法4:分别求出两个中垂线方程求出中垂线的交点坐标,得到圆心坐标求出圆心半径写出圆的方程………… 5分………… 6分………… 3分………… 4分(Ⅱ)联立圆的方程和直线方程组成的方程组消去未知数y,得到关于x的一元二次方程….7分….8分解法1:利用韦达定理,得到方程的两根和与积….9分….10分韦达定理代入上式,求出a代入△>0,验证….11分….12分解法2:求出一元二次方程的根,得到A,B坐标….9分….10分把A,B坐标代入上式,求出a验证….11分….12分解法3:求出弦长AB设AB的中点G,求出G点坐标,计算OG的长根据AB=2OG,求出a代入检验…………………..9分…………………..10分…………………..11分…………………..12分说明1.三个交点坐标若有一个对,而没有全对,给1分;
2.设圆的方程为其它非常规形式,若能解题,给分;
3.若没有圆心、半径的求解过程,扣2分;
4.若求出a=-1,又解出△>0,不扣分;
5.若第一问圆的方程有错,而第二问过程及数据没有新的错误,第二问给分不超过3分.出现的错误:4.没有对a=-1进行验证;不会处理;1.一元二次方程化简错误;3.解圆的方程组出错;2.理科21(本题满分12分,平均分4.24)已知函数 处的切线方程为 (Ⅰ)求 a,b的值;(Ⅱ)如果当 x>0,且x≠1时,求k的取值范围.评分细则(Ⅰ)解法1:…2分,且过点 (1,1),故 所以解得: b=1a=1…………3分…………4分…………5分…………6分(Ⅰ)解法2:………..2分所以又f(1)=b故曲线y=f(x)在(1,f(1))处的切线方程为与已知切线方程x+2y-3=0相比较,可得a=1,b=1………..3分………..4分………..6分(Ⅱ)解法1:由(Ⅰ)知 考虑函数 …….7分…….8分,h(x)递减 故当0
2.不理解切线的含义;
3.不能发现f(1)=1;
4.解方程组出错;
5.不会分离参数;
6.分离后的函数的单调性不会证明;
7.证明单调性不严密.文科21(本题满分12分,平均分2.06)已知函数 处的切线方程为 (Ⅰ)求 a,b的值;(Ⅱ)证明:当 x>0,且x≠1时,评分细则(Ⅰ)同理科(Ⅱ)解法1:由(Ⅰ)知 …….8分………..7分考虑函数所以当x≠1时,故当0
h(x)单调递增,h(x)
h(x)单调递增,h(x)>h(1)=0,从而当 x>0,且x≠1时,…….12分…….7分…….8分…….10分…….11分出现的错误:1.不会求导数;
2.不理解切线的含义;
3.不能发现f(1)=1;
4.解方程组出错;
5.不会作差;
6.作差后的函数的单调性不会证明.文理科22(本题满分10分,理科平均4.31分,文科平均2.14分) D,E分别为 △ABC的边 AB,AC上的点,且不与
△ABC的顶点重合.已知 AE的长为 m,AC的长为n,
AD,AB的长是关于 x的方程 x2-14x+mn=0的两个根 .(Ⅰ)证明:C,B,D,E四点共圆; (Ⅱ)若 ∠A=900,且 m=4,n=6,
求C,B,D,E所在圆的半径. 评分细则:(I)连接DE,根据题意在△ADE和△ACB中, 即……2分又∠DAE=∠CAB,从而△ADE∽△ACB
因此∠ADE=∠ACB,所以C,B,D,E四点共圆。……3分……5分(Ⅱ)解法1:m=4, n=6时,方程x2-14x+mn=0的两根
为x1=2,x2=12.故 AD=2,AB=12.……6分 取CE的中点G,DB的中点F,分别过G,F作AC,AB的
垂线,两垂线相交于H点,连接DH.因为C,B,D,E
四点共圆,所以C,B,D,E四点所在圆的圆心为H,
半径为DH. 由于∠A=900,故GH∥AB, HF∥AC. HF=AG=5,DF= 5. 故C,B,D,E四点所在圆的半径为5 ……7分……9分……10分解法2:求出AD=2,AB=12,EB=4,ED=2sin∠EDB=sin∠EDA=设C,B,D,E所在圆的半径为R,则 故C,B,D,E四点所在圆的半径为5 ……9分……10分……7分……6分解法3:以A为原点,AB所在直线为x轴,AC所在直
线为y轴建立平面直角坐标系.线段BC的中垂线方程:2x-y-9=0线段DE的中垂线方程:x-2y+3=0解方程组得x=7,y=5,所以圆心坐标为(7,5)故圆的半径为……9分……10分……7分……6分……8分解法3:以A为原点,AB所在直线为x轴,AC所在直
线为y轴建立平面直角坐标系.
则D(2,0),B(12,0),E(0,4),C(0,6)设C,B,D,E所在圆的方程为x2+y2+dx+ey+f=0将D,B,E三点的坐标代入上式,
解方程组得:d=-14,e=-10,f=24所以x2+y2-14x-10y+24=0所求半径R=……9分……10分……7分……6分说明:
1.只要有∠ADE=∠ACB,C,B,D,E四点共圆,给1分
2.正弦定理写对,给1分出现的错误:
1.三角形相似没有指出公共角;
2.切割线定理逆定理不能作为四点共圆的证明方法;
3.解方程组出现错误;
4.不会利用根与系数的关系.23 理科(本题满分12分,平均分7.27分)设函数f(x)=|x-a|+3x,其中a>0(Ⅰ)当 a=1时,求不等式f(x) ≥3x+2的解集;(Ⅱ)若不等式 f(x) ≤0的解集为{x|x≤-1},求a的值.评分细则:(Ⅰ)a=1时,不等式f(x) ≥3x+2可化为|x-1|≥2 …2分法1:由此得x-1≥2或x-1≤-2法2:两边平方得x2-2x+1≥4法3:分段讨论得{x≥1x-1≥2或{X<1x-1≤2所以x≥3或x≤-1∴不等式f(x) ≥3x+2的解集是{x|x≥3或x≤-1}…………….4分…………….5分(Ⅱ)由f(x) ≤0得: |x-a|+3x ≤0法1:此不等式可化为所以∵a>0,∴原不等式的解集为{x|x≤-a/2}由题设得-a/2=-1,∴a=2….7分….8分….9分….10分法2:此不等式可化为3x≤x-a≤-3x所以,x≤0,x≤a/4,x≤-a/2∵a>0,∴原不等式的解集为{x|x≤-a/2}….9分由题设得-a/2=-1,∴a=2….10分….8分法3:由|x-a|+3x ≤0得|x-a| ≤-3x,可化为∵a>0,∴原不等式的解集为{x|x≤-a/2}….9分由题设得-a/2=-1,∴a=2….10分….7分法4:由f(x) ≤0的解集为{x|x≤-1}所以x=-1是方程f(x) =0的根,代入得|a+1|=3∵a>0,∴a=2把a=2代入f(x) ≤0得: |x-2|+3x ≤0解此不等式得3x≤x-2≤3x,x≤-1∴当a=2时不等式 f(x) ≤0的解集为{x|x≤-1}….7分….10分说明1.不等式结果可以写成2.不写并集不给分,集合表达式不正确,不给分出现的错误:
1.不会解绝对值不等式;
2.解集形式表示有误;
3.不会分类讨论;
4.不会去掉绝对值符号.
5.不总结.㈠了解高考评分细则对教学的指导意义 ㈡制定评分细则的基本原则㈢阅卷评分的基本要求二、分析细则,感受试题1.符号图形配文字
2.呈现公式要原始
3.试题总结要牢记
4.结论证明要严密
5.简单试题写详细
6.运算结果要彻底
7.字母引入有明细
8.试题容易莫大意
9.书写规范有条理
10.将错就错没关系8分4分文科缺少过程或必要的文字说明12分4分
没有呈现等比数列的前n项
和公式的原始形式12分11分没有指出数列的前n项和即没有对Tn交代.11分
总结出错,
或没有总结没有指出棱锥的高,
或没有说明h就是
棱锥的高11分4分没有写解集9分 AD⊥BD没有证明9分AD⊥BD没有证明7分AD⊥BD没有证明,
高没有证明8分切割线定理逆定理不能作为四点共圆的证明方法10分3分 没有向量的坐标10分优质品率的计算没有过程12分12分12分12分10分10分三、规范指导,赢得试题1.重视过程完整,把握推理的严谨性
2.抓好“三基”,侧重通性通法的落实
3.书写讲究整洁,表达要有条理
4. 统筹兼顾全局,合理支配时间共轭复数打头阵,函数性质领风骚;
定义变换与对称,奇偶周期和单调;
向量三角相结合,三角公式得记牢;
框图积分三视图,新增内容头一招;
线性规划二项式,中规中矩老一套;
数列概率换模样,学生欢喜得分高;
定义性质离心率,解析几何难不倒;
轨迹切线最小值,平时训练已预料;
立体几何向量求,球体棱锥年年考。
导数压轴真给力,分类讨论弄技巧;
平面几何不等式,认真审题要选好;
不等容易几何难,忘涂题号无紧要;
今年试题显平和,师生普遍反应好;
认真分析高考题,来年命中不得了。年年岁岁题相似,岁岁年年卷不同——2012年河南省高考数学试题特点
同课章节目录
