华师大版八年级下册 18.1.1 平行四边形的性质(1) 课件(共31张PPT)
文档属性
| 名称 | 华师大版八年级下册 18.1.1 平行四边形的性质(1) 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 09:37:26 | ||
图片预览








文档简介
(共31张PPT)
18.1.1 平行四边形的性质(1)
学习目标
掌握平行四边形的概念.
探索并熟练运用平行四边形的性质.
理解两条平行线之间的距离的概念.能熟练运用平行线之间的距离的概念去解题.
两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作: ABCD
AB∥CD
AD∥BC
∵
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
几何语言:
复习回顾
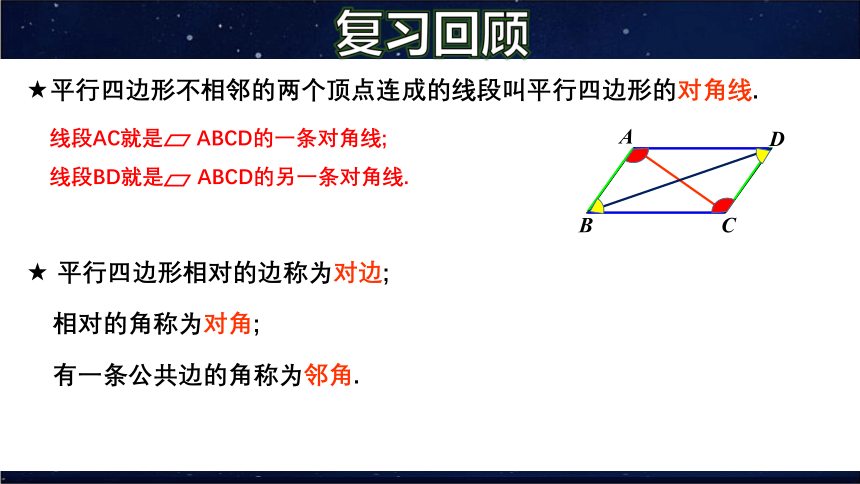
★平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
★ 平行四边形相对的边称为对边;
相对的角称为对角;
有一条公共边的角称为邻角.
A
D
C
B
复习回顾
线段AC就是 ABCD的一条对角线;
线段BD就是 ABCD的另一条对角线.
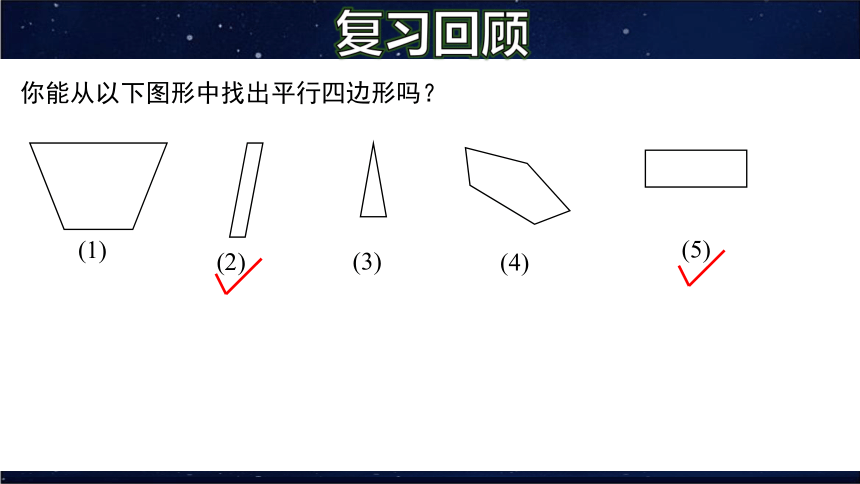
你能从以下图形中找出平行四边形吗?
(2)
(3)
(1)
(4)
(5)
复习回顾
根据定义可知平行四边形的对边互相平行.除此之外还有什么性质呢?这就是本节课要探讨的课题……
D
B
A
C
知识精讲
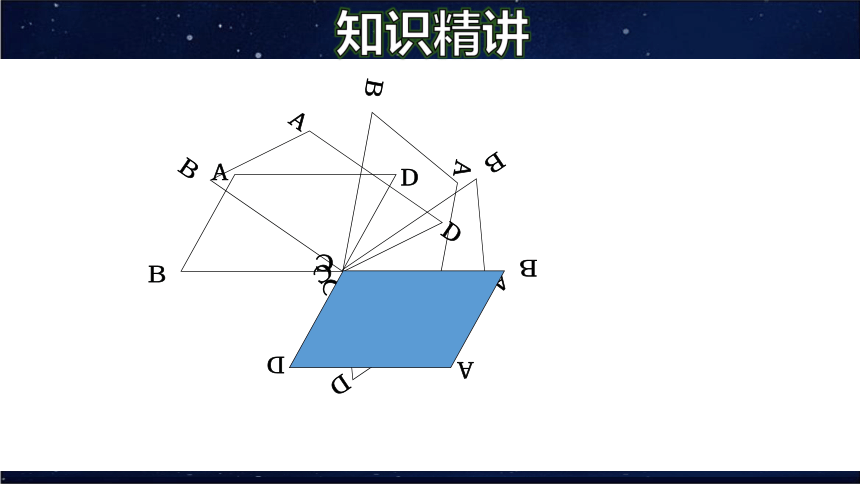
1.画一个平行四边形ABCD;
2.用一张半透明的纸复制你画的平行四边形ABCD;
3.剪下你所复制的那个平行四边形;
4.将复制后的四边形绕某个点旋转180°,你能平移该纸片,使它与原来的四边形ABCD重合吗?
知识精讲
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
知识精讲
A
B
C
D
A
B
C
D
知识精讲
猜想:
A
B
C
D
知识精讲
A
B
C
D
知识精讲
A
B
C
D
如图,已知平行四边形ABCD,其中AB // CD,AD // BC,
求证: AB=CD,AD = BC,∠ABC= ∠ADC, ∠BAD= ∠BCD.
分析:构造三角形,利用全等三角形的性质来得到对应边相等,对应角相等.在平行四边形中,连接任意一条对角线即可分成两个三角形.
知识精讲
证明:如图所示,连接AC.
A
B
C
D
⌒
⌒
⌒
⌒
1
2
3
4
∵ AB // CD,AD // BC ∴ ∠1=∠4, ∠2=∠3.
又 AC是△ABC 和△CDA的公共边,
∴△ABC≌△CDA.
∴AB=CD, AD=BC, ∠B= ∠D.
∵ ∠BAD= ∠1+∠2, ∠BCD = ∠3+∠4,
∴ ∠BAD= ∠BCD.
知识精讲
思考 不添加辅助线,你能否直接运用平行四边形的定义,证明其对角相等?
A
B
C
D
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB ∥ CD,
∴∠A+∠B=180°,
∠A+∠D=180°,
∴∠B=∠D.
同理可得∠A=∠C.
知识精讲
几何语言:
平行四边形定理1:平行四边形的两组对边分别相等.
在 ABCD中,
AB=CD,AD=BC.(平行四边形的对边相等)
∠A=∠C, ∠B=∠D
(平行四边形的对角相等)
∠A+∠B=180° ∠A+∠D =180°
(平行四边的邻角互补)
平行四边形定理2:平行四边形的两组对角分别相等.
推论: 平行四边的邻角互补.
知识精讲
例1 如图,在 ABCD中, ∠A =40。.求其他各内角的大小.
∵四边形ABCD是平行四边形
解:
且 ∠A =40。(已知),
∴ ∠A = ∠C=40。, ∠B= ∠D (平行四边形的对角相等).
又∵AD∥BC(平行四边形的对边平行),
∴ ∠A + ∠B =180。(两直线平行,同旁内角互补),
∴ ∠B= ∠D= 180。- ∠A = 180。- 40。=140。
典例解析
D
A
B
C
例2 如图,在 ABCD中, AB=8,周长等于24.求余各边的长.
∵四边形ABCD是平行四边形
解:
且 AB =8(已知),
∴ DC = AB=8, AD= BC (平行四边形的对边相等).
又∵周长等于24,
∴ AB+BC+DC+AD=24,
∴ AD= BC= (24-2AB)= 4.
典例解析
D
A
B
C
1.如图:在 ABCD中,根据平行四边形的性质,求出其他边的长度和角的度数.
32cm
30cm
32cm
30cm
A
B
C
D
56°
56°
124°
124°
针对练习
2.如图,四边形ABCD是平行四边形,则:
1)∠ADC=_________, ∠BCD= ;
2)边AB= , BC = .
D
C
B
A
58°
28
32
58°
28
32
122°
28
32
针对练习
在笔直的铁轨上, 夹在两根铁轨之间的枕木是否一样长
知识精讲
C
B
F
E
A
D
若m // n,作 AB // CD // EF,分别交 m于A、C、E,交 n于B、D、F.
由平行四边形的性质得AB=CD=EF.
两条平行线之间的平行线段相等.
m
n
由平行四边形的定义易知四边形ABCD,CDEF均为平行四边形.
知识精讲
两条平行线间的距离相等.
若m // n,AB、CD、EF垂直于 n,交n于B、D、F,交 m于A、C、E.
B
F
E
A
n
m
C
D
点到直线的距离
同前面易得AB=CD=EF
两条平行线间的距离:两条平行线中,一条直线上任意一点到另一条直线的距离
知识精讲
两条平行线之间的距离
两条平行线之间的距离:两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
数学语言:a//b,A是a上的任意一点,AB⊥b,B是垂足,线段AB的长就是a、b之间的距离.
a
b
A
┐
B
知识精讲
距离 两点间的距离 点到直线的距离 两条平行线之间的距离
区别
联系
连接两点的线段的长度
点到直线的垂线段的长度
两条平行线中,从一条直线上任一点到另一条直线的垂线段的长度
都是指某一条线段的长度
知识精讲
性质:如果两条直线平行,那么一条直线上所有的点到另一条直线的距离都相等,即平行线间的距离处处相等.
数学语言:如图所示,A、C是直线l1上的任意两点.
l1
l2
A
B
┐
┐
C
D
∵ l1 // l2 ,AB⊥ l2 ,CD⊥ l2 ,
∴ AB=CD.
知识精讲
如图,AB∥CD,BC⊥AB,若AB=4cm,S△ABC=12cm2,求△ABD中AB边上的高.
解:S△ABC = AB BC,
= ×4 ×BC=12cm2,
∴BC=6cm.
∵AB∥CD,
∴点D到AB边的距离等于BC的长度,
∴△ABD中AB边上的高为6cm.
针对练习
A
B
D
C
E
9cm
5cm
1.如图所示,若BE平分∠ABC,则ED= .
4cm
2
3
5cm
5cm
4cm
1
达标检测
3cm
A
B
D
C
5cm
4cm
2.求如图所示的四边形ABCD的面积.
3cm
达标检测
3.如图,已知AD//BC,判断S△ABC和S△DBC是否相等,并说明理由.
A
B
C
D
解:由图可知,△ABC 和△DBC 有一条公共边BC
∵ AD//BC
∴ 点D、点A到BC的距离相等
∴ △ABC 和△DBC 同底等高,面积相等.
达标检测
4.如图:小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少
解:∵ 四边形ABCD是平行四边形
∴AB=CD, AD=BC
∵AB=8m
∴CD=8m
又AB+BC+CD+AD=36,
∴ AD=BC=10m
A
D
B
C
8cm
达标检测
18.1.1 平行四边形的性质(1)
学习目标
掌握平行四边形的概念.
探索并熟练运用平行四边形的性质.
理解两条平行线之间的距离的概念.能熟练运用平行线之间的距离的概念去解题.
两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作: ABCD
AB∥CD
AD∥BC
∵
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
几何语言:
复习回顾
★平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
★ 平行四边形相对的边称为对边;
相对的角称为对角;
有一条公共边的角称为邻角.
A
D
C
B
复习回顾
线段AC就是 ABCD的一条对角线;
线段BD就是 ABCD的另一条对角线.
你能从以下图形中找出平行四边形吗?
(2)
(3)
(1)
(4)
(5)
复习回顾
根据定义可知平行四边形的对边互相平行.除此之外还有什么性质呢?这就是本节课要探讨的课题……
D
B
A
C
知识精讲
1.画一个平行四边形ABCD;
2.用一张半透明的纸复制你画的平行四边形ABCD;
3.剪下你所复制的那个平行四边形;
4.将复制后的四边形绕某个点旋转180°,你能平移该纸片,使它与原来的四边形ABCD重合吗?
知识精讲
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
知识精讲
A
B
C
D
A
B
C
D
知识精讲
猜想:
A
B
C
D
知识精讲
A
B
C
D
知识精讲
A
B
C
D
如图,已知平行四边形ABCD,其中AB // CD,AD // BC,
求证: AB=CD,AD = BC,∠ABC= ∠ADC, ∠BAD= ∠BCD.
分析:构造三角形,利用全等三角形的性质来得到对应边相等,对应角相等.在平行四边形中,连接任意一条对角线即可分成两个三角形.
知识精讲
证明:如图所示,连接AC.
A
B
C
D
⌒
⌒
⌒
⌒
1
2
3
4
∵ AB // CD,AD // BC ∴ ∠1=∠4, ∠2=∠3.
又 AC是△ABC 和△CDA的公共边,
∴△ABC≌△CDA.
∴AB=CD, AD=BC, ∠B= ∠D.
∵ ∠BAD= ∠1+∠2, ∠BCD = ∠3+∠4,
∴ ∠BAD= ∠BCD.
知识精讲
思考 不添加辅助线,你能否直接运用平行四边形的定义,证明其对角相等?
A
B
C
D
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB ∥ CD,
∴∠A+∠B=180°,
∠A+∠D=180°,
∴∠B=∠D.
同理可得∠A=∠C.
知识精讲
几何语言:
平行四边形定理1:平行四边形的两组对边分别相等.
在 ABCD中,
AB=CD,AD=BC.(平行四边形的对边相等)
∠A=∠C, ∠B=∠D
(平行四边形的对角相等)
∠A+∠B=180° ∠A+∠D =180°
(平行四边的邻角互补)
平行四边形定理2:平行四边形的两组对角分别相等.
推论: 平行四边的邻角互补.
知识精讲
例1 如图,在 ABCD中, ∠A =40。.求其他各内角的大小.
∵四边形ABCD是平行四边形
解:
且 ∠A =40。(已知),
∴ ∠A = ∠C=40。, ∠B= ∠D (平行四边形的对角相等).
又∵AD∥BC(平行四边形的对边平行),
∴ ∠A + ∠B =180。(两直线平行,同旁内角互补),
∴ ∠B= ∠D= 180。- ∠A = 180。- 40。=140。
典例解析
D
A
B
C
例2 如图,在 ABCD中, AB=8,周长等于24.求余各边的长.
∵四边形ABCD是平行四边形
解:
且 AB =8(已知),
∴ DC = AB=8, AD= BC (平行四边形的对边相等).
又∵周长等于24,
∴ AB+BC+DC+AD=24,
∴ AD= BC= (24-2AB)= 4.
典例解析
D
A
B
C
1.如图:在 ABCD中,根据平行四边形的性质,求出其他边的长度和角的度数.
32cm
30cm
32cm
30cm
A
B
C
D
56°
56°
124°
124°
针对练习
2.如图,四边形ABCD是平行四边形,则:
1)∠ADC=_________, ∠BCD= ;
2)边AB= , BC = .
D
C
B
A
58°
28
32
58°
28
32
122°
28
32
针对练习
在笔直的铁轨上, 夹在两根铁轨之间的枕木是否一样长
知识精讲
C
B
F
E
A
D
若m // n,作 AB // CD // EF,分别交 m于A、C、E,交 n于B、D、F.
由平行四边形的性质得AB=CD=EF.
两条平行线之间的平行线段相等.
m
n
由平行四边形的定义易知四边形ABCD,CDEF均为平行四边形.
知识精讲
两条平行线间的距离相等.
若m // n,AB、CD、EF垂直于 n,交n于B、D、F,交 m于A、C、E.
B
F
E
A
n
m
C
D
点到直线的距离
同前面易得AB=CD=EF
两条平行线间的距离:两条平行线中,一条直线上任意一点到另一条直线的距离
知识精讲
两条平行线之间的距离
两条平行线之间的距离:两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
数学语言:a//b,A是a上的任意一点,AB⊥b,B是垂足,线段AB的长就是a、b之间的距离.
a
b
A
┐
B
知识精讲
距离 两点间的距离 点到直线的距离 两条平行线之间的距离
区别
联系
连接两点的线段的长度
点到直线的垂线段的长度
两条平行线中,从一条直线上任一点到另一条直线的垂线段的长度
都是指某一条线段的长度
知识精讲
性质:如果两条直线平行,那么一条直线上所有的点到另一条直线的距离都相等,即平行线间的距离处处相等.
数学语言:如图所示,A、C是直线l1上的任意两点.
l1
l2
A
B
┐
┐
C
D
∵ l1 // l2 ,AB⊥ l2 ,CD⊥ l2 ,
∴ AB=CD.
知识精讲
如图,AB∥CD,BC⊥AB,若AB=4cm,S△ABC=12cm2,求△ABD中AB边上的高.
解:S△ABC = AB BC,
= ×4 ×BC=12cm2,
∴BC=6cm.
∵AB∥CD,
∴点D到AB边的距离等于BC的长度,
∴△ABD中AB边上的高为6cm.
针对练习
A
B
D
C
E
9cm
5cm
1.如图所示,若BE平分∠ABC,则ED= .
4cm
2
3
5cm
5cm
4cm
1
达标检测
3cm
A
B
D
C
5cm
4cm
2.求如图所示的四边形ABCD的面积.
3cm
达标检测
3.如图,已知AD//BC,判断S△ABC和S△DBC是否相等,并说明理由.
A
B
C
D
解:由图可知,△ABC 和△DBC 有一条公共边BC
∵ AD//BC
∴ 点D、点A到BC的距离相等
∴ △ABC 和△DBC 同底等高,面积相等.
达标检测
4.如图:小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少
解:∵ 四边形ABCD是平行四边形
∴AB=CD, AD=BC
∵AB=8m
∴CD=8m
又AB+BC+CD+AD=36,
∴ AD=BC=10m
A
D
B
C
8cm
达标检测
