华师大版八年级下册 18.2.1 平行四边形的判定(1) 课件(共27张PPT)
文档属性
| 名称 | 华师大版八年级下册 18.2.1 平行四边形的判定(1) 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 09:43:23 | ||
图片预览





文档简介
(共27张PPT)
18.2.1 平行四边形的判定(1)
学习目标
理解并掌握平行四边形的判定方法1、2.
能灵活利用平行四边形的判定方法1、2解决问题.
复习回顾
两组对边分别是平行的,所以由定义可以判定四边形是否是平行四边形.
我们由平行四边形的定义知道:
两组对边分别平行
平行四边形
性质
判别
定义既是性质,也是判定方法.
知识精讲
有一天,李老师的儿子从幼儿园放学来到办公室,看到郑老师办公桌上一块平行四边形纸片,于是就拿起笔来画画,画了一会儿,对自已的作品不满意撕去了一些,巧的是刚好从A、C两个顶点撕开.你只有两把没刻度的直尺,你能帮它补好吗?
A
B
C
D
∵AB∥CD,BC ∥AD,
∴四边形ABCD是平行四边形.
针对练行四边形的性质“平行四边形的两组对边分别相等”,逆向思考,互换条件与结论,试写出它的逆命题.你认为它是一个这个真命题吗?
知识精讲
两组对边分别相等
四边形是平行四边形
两组对边分别相等的四边形
四边形是平行四边形
知识精讲
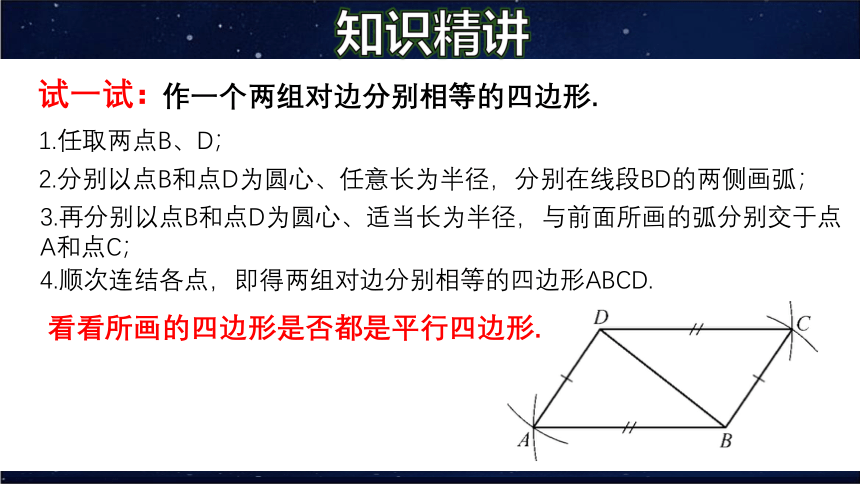
试一试:
作一个两组对边分别相等的四边形.
1.任取两点B、D;
2.分别以点B和点D为圆心、任意长为半径,分别在线段BD的两侧画弧;
3.再分别以点B和点D为圆心、适当长为半径,与前面所画的弧分别交于点A和点C;
4.顺次连结各点,即得两组对边分别相等的四边形ABCD.
看看所画的四边形是否都是平行四边形.
知识精讲
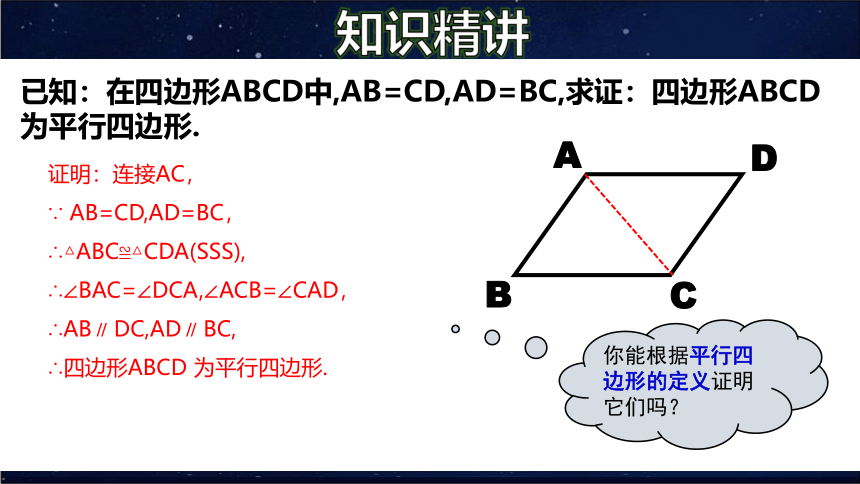
已知:在四边形ABCD中,AB=CD,AD=BC,求证:四边形ABCD 为平行四边形.
A
B
C
D
证明:连接AC,
∵ AB=CD,AD=BC,
∴△ABC≌△CDA(SSS),
∴∠BAC=∠DCA,∠ACB=∠CAD,
∴AB∥ DC,AD∥ BC,
∴四边形ABCD 为平行四边形.
你能根据平行四边形的定义证明它们吗?
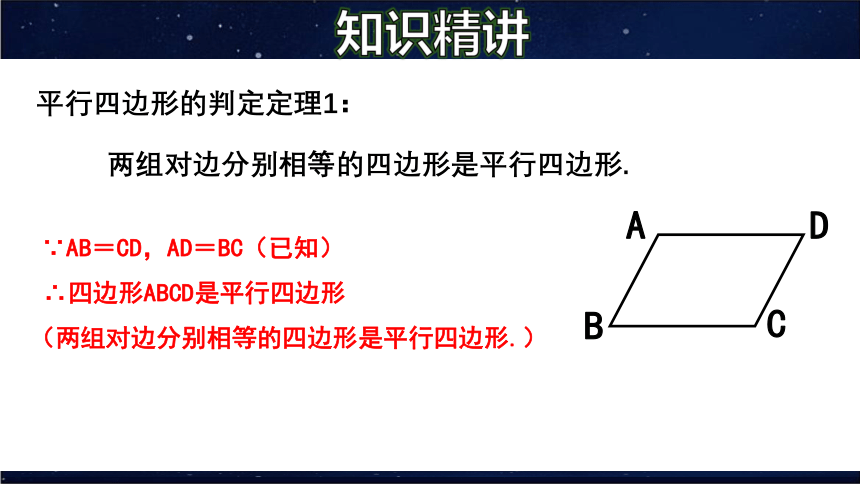
平行四边形的判定定理1:
两组对边分别相等的四边形是平行四边形.
A
B
C
D
∵AB=CD,AD=BC(已知)
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形.)
知识精讲
例1 如图,在Rt△MON中,∠MON=90°.求证:四边形PONM是平行四边形.
证明:Rt△MON中,
由勾股定理得(x-5)2+42=(x-3)2,
解得x=8.
∴PM=11-x=3,ON=x-5=3,MN=x-3=5.
∴PM=ON,OP=MN,
∴四边形PONM是平行四边形.
典例解析
1.如图,AB =DC=EF, AD=BC,DE=CF,则图中有哪些互相平行的线段?
AB ∥ DC∥ EF
AD ∥ BC
DE ∥ CF
针对练习
2.如图, AD⊥AC,BC⊥AC,且AB=CD,求证:四边形ABCD是平行四边形.
证明:在Rt△ABC和Rt△ACD中,
∵AC=CA,AB=CD,
∴Rt△ABC≌Rt△CDA(HL),
∴BC=DA.
又∵AB=CD,
∴四边形PONM是平行四边形.
针对练习
将一根木棒从AB平移到DC,AB与DC之间的位置关系、数量关系?
A
B
C
D
四边形ABCD是什么样的图形?
猜想:一组对边平行且相等的四边形是平行四边形.
知识精讲
知识精讲
已知:在四边形ABCD中,AB=DC,AB∥DC,求证:四边形ABCD 为平行四边形.
A
B
C
D
证明:连接AC,
∵ AB∥DC,
∴∠BAC=∠DCA,
∵ AB=DC,AC=CA,
∴△ABC≌△CDA(SAS),
∴BC=AD,
∴四边形ABCD 为平行四边形.
∵ AD∥CB,AD= BC,
∴ 四边形ABCD是平行四边形.
C
B
D
A
平行四边形的判定定理2:
一组对边平行且相等的四边形是平行四边形.
知识精讲
一组对边平行,另一组对边相等的四边形是平行四边形.
命题:
C
B
D
A
C
B
D
A
是假命题
知识精讲
典例解析
例2 已知:如图,在□ABCD中,点E、F分别在对边BC和DA上,且AF=CE.
求证:四边形AECF是平行四边形.
E
F
D
C
B
A
证明:∵四边形ABCD 为平行四边形,
∴AD∥ CB(平行四边形的对边平行),
即AF ∥ CE.
∵ BF=DE,
又∵ AF= CE ,
∴四边形AECF 为平行四边形.
如图,AC∥ED,点B在AC上且AB=ED=BC .找出图中的平行四边形.
A
C
B
E
D
解:四边形ABDE,BCDE都是平行四边形,理由是:
∵ AB∥ED AB=ED
∴四边形ABDE是平行四边形
( 一组对边平行且相等的四边形平行四边形 )
∵ BC∥ED BC=ED
∴四边形BCDE是平行四边形
( 一组对边平行且相等的四边形平行四边形 )
针对练习
1.已知四边形ABCD中有四个条件:AB∥CD,AB=CD,BC∥AD,BC=AD,从中任选两个,不能使四边形ABCD成为平行四边形的选法是 ( )
A.AB∥CD,AB=CD
B.AB∥CD,BC∥AD
C.AB∥CD,BC=AD
D.AB=CD,BC=AD
C
达标检测
2.如图,已知E,F,G,H分别是 ABCD的边AB,BC,CD,DA上的点,且AE=CG,BF=DH.求证:四边形EFGH是平行四边形.
证明:在平行四边形ABCD中,
∠A=∠C,AD=BC,
又∵BF=DH,
∴AH=CF.
又∵AE=CG,
∴△AEH≌△CGF(SAS),
∴EH=GF.
同理得△BEF≌△DGH(SAS),
∴GH=EF,
∴四边形EFGH是平行四边形.
达标检测
A
B
C
D
E
F
证明:∵四边形AEFD和EBCF都是平行四边形,
∴AD∥ EF,AD=EF,
EF∥ BC, EF=BC.
∴AD∥ BC,AD=BC.
∴四边形ABCD是平行四边形.
3.四边形AEFD和EBCF都是平行四边形,求证:四边形ABCD 是平行四边形.
达标检测
4.如图,点C是AB的中点,AD=CE,CD=BE.
(1)求证:△ACD≌△CBE;
(2)求证:四边形CBED是平行四边形.
证明:(1)∵点C是AB的中点,∴AC=BC.
在△ADC与△CEB中,
AD=CE , CD=BE , AC=BC ,
∴△ADC≌△CEB(SSS),
(2)∵△ADC≌△CEB,
∴∠ACD=∠CBE,
∴CD∥BE.
又∵CD=BE,
∴四边形CBED是平行四边形.
达标检测
5.如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,AE=DF,∠A=∠D,AB=DC.求证:四边形BFCE是平行四边形.
证明:∵AB=CD,
∴AB+BC=CD+BC,即AC=BD,
在△ACE和△DBF中,
AC=BD ,∠A=∠D, AE=DF ,
∴△ACE≌△DBF(SAS),
∴CE=BF,∠ACE=∠DBF,
∴CE∥BF,
∴四边形BFCE是平行四边形.
达标检测
D
A
B
C
E
F
证明:
四边形ABCD是平行四边形
AD ∥ BC且AD =BC
EAD= FCB
AE=CF
EAD= FCB
AD=BC
AED ≌ CFB(SAS)
DE=BF
四边形BFDE是平行四边形
在 AED和 CFB中
同理可证:BE=DF
6.已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形。
达标检测
平行四边形的判定定理1:
两组对边分别相等的四边形是平行四边形.
A
B
C
D
∵AB=CD,AD=BC(已知)
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形.)
小结梳理
∵ AD∥CB,AD= BC,
∴ 四边形ABCD是平行四边形.
C
B
D
A
平行四边形的判定定理2:
一组对边平行且相等的四边形是平行四边形.
小结梳理
18.2.1 平行四边形的判定(1)
学习目标
理解并掌握平行四边形的判定方法1、2.
能灵活利用平行四边形的判定方法1、2解决问题.
复习回顾
两组对边分别是平行的,所以由定义可以判定四边形是否是平行四边形.
我们由平行四边形的定义知道:
两组对边分别平行
平行四边形
性质
判别
定义既是性质,也是判定方法.
知识精讲
有一天,李老师的儿子从幼儿园放学来到办公室,看到郑老师办公桌上一块平行四边形纸片,于是就拿起笔来画画,画了一会儿,对自已的作品不满意撕去了一些,巧的是刚好从A、C两个顶点撕开.你只有两把没刻度的直尺,你能帮它补好吗?
A
B
C
D
∵AB∥CD,BC ∥AD,
∴四边形ABCD是平行四边形.
针对练行四边形的性质“平行四边形的两组对边分别相等”,逆向思考,互换条件与结论,试写出它的逆命题.你认为它是一个这个真命题吗?
知识精讲
两组对边分别相等
四边形是平行四边形
两组对边分别相等的四边形
四边形是平行四边形
知识精讲
试一试:
作一个两组对边分别相等的四边形.
1.任取两点B、D;
2.分别以点B和点D为圆心、任意长为半径,分别在线段BD的两侧画弧;
3.再分别以点B和点D为圆心、适当长为半径,与前面所画的弧分别交于点A和点C;
4.顺次连结各点,即得两组对边分别相等的四边形ABCD.
看看所画的四边形是否都是平行四边形.
知识精讲
已知:在四边形ABCD中,AB=CD,AD=BC,求证:四边形ABCD 为平行四边形.
A
B
C
D
证明:连接AC,
∵ AB=CD,AD=BC,
∴△ABC≌△CDA(SSS),
∴∠BAC=∠DCA,∠ACB=∠CAD,
∴AB∥ DC,AD∥ BC,
∴四边形ABCD 为平行四边形.
你能根据平行四边形的定义证明它们吗?
平行四边形的判定定理1:
两组对边分别相等的四边形是平行四边形.
A
B
C
D
∵AB=CD,AD=BC(已知)
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形.)
知识精讲
例1 如图,在Rt△MON中,∠MON=90°.求证:四边形PONM是平行四边形.
证明:Rt△MON中,
由勾股定理得(x-5)2+42=(x-3)2,
解得x=8.
∴PM=11-x=3,ON=x-5=3,MN=x-3=5.
∴PM=ON,OP=MN,
∴四边形PONM是平行四边形.
典例解析
1.如图,AB =DC=EF, AD=BC,DE=CF,则图中有哪些互相平行的线段?
AB ∥ DC∥ EF
AD ∥ BC
DE ∥ CF
针对练习
2.如图, AD⊥AC,BC⊥AC,且AB=CD,求证:四边形ABCD是平行四边形.
证明:在Rt△ABC和Rt△ACD中,
∵AC=CA,AB=CD,
∴Rt△ABC≌Rt△CDA(HL),
∴BC=DA.
又∵AB=CD,
∴四边形PONM是平行四边形.
针对练习
将一根木棒从AB平移到DC,AB与DC之间的位置关系、数量关系?
A
B
C
D
四边形ABCD是什么样的图形?
猜想:一组对边平行且相等的四边形是平行四边形.
知识精讲
知识精讲
已知:在四边形ABCD中,AB=DC,AB∥DC,求证:四边形ABCD 为平行四边形.
A
B
C
D
证明:连接AC,
∵ AB∥DC,
∴∠BAC=∠DCA,
∵ AB=DC,AC=CA,
∴△ABC≌△CDA(SAS),
∴BC=AD,
∴四边形ABCD 为平行四边形.
∵ AD∥CB,AD= BC,
∴ 四边形ABCD是平行四边形.
C
B
D
A
平行四边形的判定定理2:
一组对边平行且相等的四边形是平行四边形.
知识精讲
一组对边平行,另一组对边相等的四边形是平行四边形.
命题:
C
B
D
A
C
B
D
A
是假命题
知识精讲
典例解析
例2 已知:如图,在□ABCD中,点E、F分别在对边BC和DA上,且AF=CE.
求证:四边形AECF是平行四边形.
E
F
D
C
B
A
证明:∵四边形ABCD 为平行四边形,
∴AD∥ CB(平行四边形的对边平行),
即AF ∥ CE.
∵ BF=DE,
又∵ AF= CE ,
∴四边形AECF 为平行四边形.
如图,AC∥ED,点B在AC上且AB=ED=BC .找出图中的平行四边形.
A
C
B
E
D
解:四边形ABDE,BCDE都是平行四边形,理由是:
∵ AB∥ED AB=ED
∴四边形ABDE是平行四边形
( 一组对边平行且相等的四边形平行四边形 )
∵ BC∥ED BC=ED
∴四边形BCDE是平行四边形
( 一组对边平行且相等的四边形平行四边形 )
针对练习
1.已知四边形ABCD中有四个条件:AB∥CD,AB=CD,BC∥AD,BC=AD,从中任选两个,不能使四边形ABCD成为平行四边形的选法是 ( )
A.AB∥CD,AB=CD
B.AB∥CD,BC∥AD
C.AB∥CD,BC=AD
D.AB=CD,BC=AD
C
达标检测
2.如图,已知E,F,G,H分别是 ABCD的边AB,BC,CD,DA上的点,且AE=CG,BF=DH.求证:四边形EFGH是平行四边形.
证明:在平行四边形ABCD中,
∠A=∠C,AD=BC,
又∵BF=DH,
∴AH=CF.
又∵AE=CG,
∴△AEH≌△CGF(SAS),
∴EH=GF.
同理得△BEF≌△DGH(SAS),
∴GH=EF,
∴四边形EFGH是平行四边形.
达标检测
A
B
C
D
E
F
证明:∵四边形AEFD和EBCF都是平行四边形,
∴AD∥ EF,AD=EF,
EF∥ BC, EF=BC.
∴AD∥ BC,AD=BC.
∴四边形ABCD是平行四边形.
3.四边形AEFD和EBCF都是平行四边形,求证:四边形ABCD 是平行四边形.
达标检测
4.如图,点C是AB的中点,AD=CE,CD=BE.
(1)求证:△ACD≌△CBE;
(2)求证:四边形CBED是平行四边形.
证明:(1)∵点C是AB的中点,∴AC=BC.
在△ADC与△CEB中,
AD=CE , CD=BE , AC=BC ,
∴△ADC≌△CEB(SSS),
(2)∵△ADC≌△CEB,
∴∠ACD=∠CBE,
∴CD∥BE.
又∵CD=BE,
∴四边形CBED是平行四边形.
达标检测
5.如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,AE=DF,∠A=∠D,AB=DC.求证:四边形BFCE是平行四边形.
证明:∵AB=CD,
∴AB+BC=CD+BC,即AC=BD,
在△ACE和△DBF中,
AC=BD ,∠A=∠D, AE=DF ,
∴△ACE≌△DBF(SAS),
∴CE=BF,∠ACE=∠DBF,
∴CE∥BF,
∴四边形BFCE是平行四边形.
达标检测
D
A
B
C
E
F
证明:
四边形ABCD是平行四边形
AD ∥ BC且AD =BC
EAD= FCB
AE=CF
EAD= FCB
AD=BC
AED ≌ CFB(SAS)
DE=BF
四边形BFDE是平行四边形
在 AED和 CFB中
同理可证:BE=DF
6.已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形。
达标检测
平行四边形的判定定理1:
两组对边分别相等的四边形是平行四边形.
A
B
C
D
∵AB=CD,AD=BC(已知)
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形.)
小结梳理
∵ AD∥CB,AD= BC,
∴ 四边形ABCD是平行四边形.
C
B
D
A
平行四边形的判定定理2:
一组对边平行且相等的四边形是平行四边形.
小结梳理
