19.2.1第2课时 正比例函数的图象和性质 课件(共26页)
文档属性
| 名称 | 19.2.1第2课时 正比例函数的图象和性质 课件(共26页) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-27 15:29:06 | ||
图片预览





文档简介
(共26张PPT)
人教版八下数学
精品同步教学课件
19.2.1 正比例函数
第2课时 正比例函数的图象和性质
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础水平的学生使用。课件包括以下环节:
新知引入
典例分析
自主学习
随堂练习
拓展提高
课堂小结
备选习题
列表
描点
连线
问题1:下列函数哪些是正比例函数?
(1)y=-3x ; (2)y= x + 3;
(3)y= 4x; (4)y= x2.
问题2:描点法画函数图象的三个步骤是
_______、_______、_______.
(1)(3)
问题引入
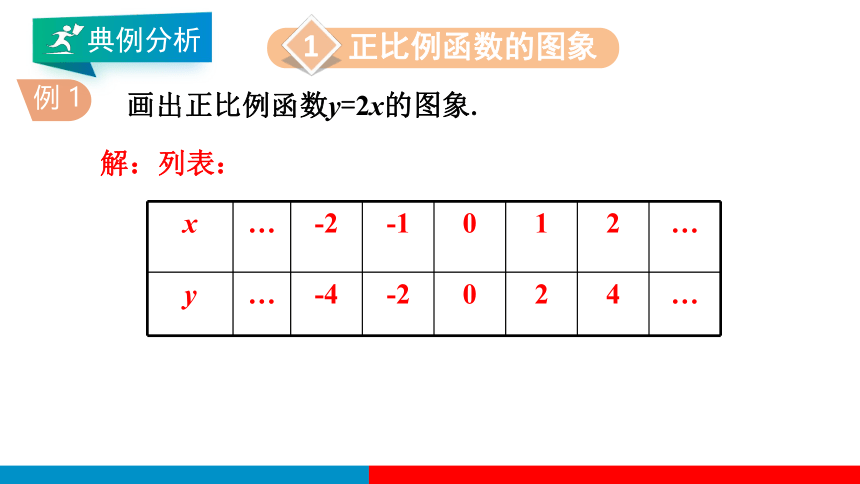
例 1
画出正比例函数y=2x的图象.
x … -2 -1 0 1 2 …
y … -4 -2 0 2 4 …
解:列表:
正比例函数的图象
1
典例分析
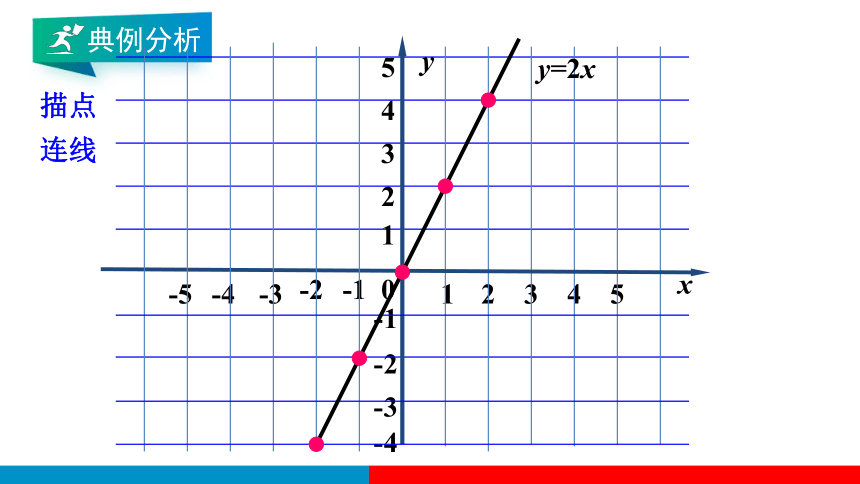
描点
连线
-4
-3
-2
-1
5
4
3
2
1
-1 0
-2
-3
-4
-5
2
3
4
5
y
1
y=2x
x
典例分析
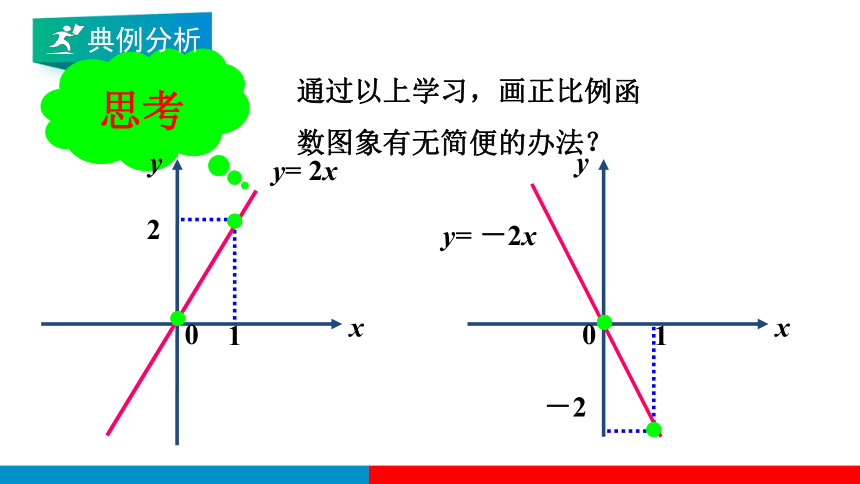
通过以上学习,画正比例函
数图象有无简便的办法?
思考
x
y
0
x
y
0
1
1
y= 2x
y= -2x
-2
2
典例分析
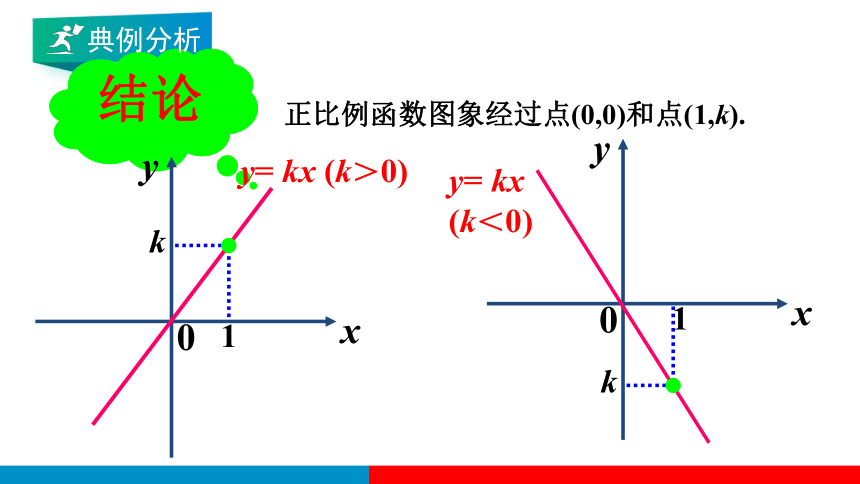
正比例函数图象经过点(0,0)和点(1,k).
结论
x
y
0
x
y
0
1
k
1
k
y= kx (k>0)
y= kx
(k<0)
典例分析
因为正比例函数的图像是一条直线,而两点确定一条直线.
画正比例函数的图像时,只需描两个点,然后过这两个点画一条直线.
典例分析
例2
画出下列正比例函数的图象:
(1) y=2x, y= x;(2) y=-1.5x, y=-4x.
解:
(1)函数y=2x中自变量x可为任意实数.下表是y与x
的几组对应值.
x … -3 -2 -1 0 1 2 3 …
y … -6 -4 -2 0 2 4 6 …
典例分析
如图所示,在直角坐标系中描出以表
中的值为坐标的点.将这些点连接起来,得到一条经
过原点和第三、第一象限的直线.它就是函数y=2x
的图象.
用同样的方法,可以得到
函数y= 的图象(如图).
它也是一条经过原点和第
三、第一象限的直线.
典例分析
如图,在直角坐标系中描出
以表中的值为坐标的点.将这
些点连接起来,得到一条经
过原点和第二、第四象限的
直线,它就是函数y=-1.5x
的图象.
用同样的方法,可以得到函数 y=-4x的图象(如
图). 它也是一条经过原点和第二、第四象限的直线.
典例分析
1.
用你认为最简单的方法画出下列函数的图象:
(1) (2) y=-3x.
解:函数y= x与函数y=-3x均
可以用两点法画图象,列表:
x 0 1
y= x 0
y=-3x 0 -3
描点连线,图象如图所示.
课堂练习
正比例函数的性质
2
在同一直角坐标系内画出正比例函数y=3x,
y=x, y= x的图象.
当k>0时,它的图像 经过第一、三象限.
1
y
x
o
3
3
1
自主学习
当k<0时,它的图像经过第二、四象限
在同一坐标系内画下列正比例函数的图像:
知识点
1
y
x
o
自主学习
自主学习
当k>0时,正比例函数的图像经过第一、三象限,
自变量x逐渐增大时,y的值也随着逐渐增大.
(2) 当k<0时,正比例函数的图像经过第二、四象限,
自变量x逐渐增大时,y的值则随着逐渐减小.
自主学习
x
y
0
1
1
当 |k| 越大时,
图像越靠近y轴
当 |k| 相等时,
图像关于坐标
轴对称
自主学习
例 3
〈珠海〉已知函数y=3x的图象经过点A(-1,y1),点B(-2,y2),则y1______y2(填“>”“<”或“=”).
导引:
方法一:把点A、点B的坐标分别代入函数
y=3x,求出y1,y2的值比较大小即可.
方法二:画出正比例函数y=3x的图象,在
函数图象上标出点A、点B,利用数形结合
思想来比较y1,y2的大小.如图,观察图形,
显然可得y1>y2.
>
典例分析
方法三:根据正比例函数的增减性来比较函数值的大小.
根据正比例函数的性质,当k>0时,y随x的增大而增大,
即可得y1>y2.
典例分析
归 纳
正比例函数图象上两点的纵坐标的大小与比例
系数及自变量的大小有关;比例系数是正数时,函
数值随自变量的增大而增大;比例系数是负数时,
函数值随自变量的增大而减小.本例的解法中,方
法一是利用求值比较法;方法二是利用数形结合思
想,用“形”上的点的位置来比较“数”的大小;
方法三是利用函数的增减性来比较大小.
典例分析
1.
已知正比例函数y=(k+5)x,且y随x的增大而减小,则k的取值范围是( )
A.k>5 B.k<5
C.k>-5 D.k<-5
D
课堂练习
2.
关于函数y=-2x,下列判断正确的是( )
A.图象经过第一、三象限
B.y随x的增大而增大
C.若(x1,y1),(x2,y2)是该函数图象上的两点,
则当x1y2
D.不论x为何值,总有y<0
C
课堂练习
3.
【中考·茂名】如图,三个正比例函数的图象分别对应解析式:①y=ax;②y=bx;③y=cx,将a,b,c从小到大排列并用“<”连接为___________.
a<c<b
课堂练习
4. 如图分别是函数y=k1 x,y=k2 x,y=k3 x,y=k4 x的图象.
(1)k1 k2,k3 k4(填“>”或“<”或“=”);
(2)用不等号将k1, k2, k3, k4及0依次连接起来.
<
解: k1<k2 <0<k3 <k4
4
2
-2
-4
4
x
y
O
y =k4 x
-4
-2
2
y =k3 x
y =k2 x
y =k1 x
<
课堂练习
正比例函数的
图象和性质
图象:正比例函数y=kx(k是常数,k≠0)的图象是
一条经过原点的直线,我们称它为直线y=kx.
性质:
当k>0时,直线y=kx经过第一、三象限,从
左向右上升,y随着x的增大而增大;
当k<0时,直线y=kx经过第二、四象限,从
左向右下降,y随着x的增大而减小.
https://www.21cnjy.com/help/help_extract.php
人教版八下数学
精品同步教学课件
19.2.1 正比例函数
第2课时 正比例函数的图象和性质
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础水平的学生使用。课件包括以下环节:
新知引入
典例分析
自主学习
随堂练习
拓展提高
课堂小结
备选习题
列表
描点
连线
问题1:下列函数哪些是正比例函数?
(1)y=-3x ; (2)y= x + 3;
(3)y= 4x; (4)y= x2.
问题2:描点法画函数图象的三个步骤是
_______、_______、_______.
(1)(3)
问题引入
例 1
画出正比例函数y=2x的图象.
x … -2 -1 0 1 2 …
y … -4 -2 0 2 4 …
解:列表:
正比例函数的图象
1
典例分析
描点
连线
-4
-3
-2
-1
5
4
3
2
1
-1 0
-2
-3
-4
-5
2
3
4
5
y
1
y=2x
x
典例分析
通过以上学习,画正比例函
数图象有无简便的办法?
思考
x
y
0
x
y
0
1
1
y= 2x
y= -2x
-2
2
典例分析
正比例函数图象经过点(0,0)和点(1,k).
结论
x
y
0
x
y
0
1
k
1
k
y= kx (k>0)
y= kx
(k<0)
典例分析
因为正比例函数的图像是一条直线,而两点确定一条直线.
画正比例函数的图像时,只需描两个点,然后过这两个点画一条直线.
典例分析
例2
画出下列正比例函数的图象:
(1) y=2x, y= x;(2) y=-1.5x, y=-4x.
解:
(1)函数y=2x中自变量x可为任意实数.下表是y与x
的几组对应值.
x … -3 -2 -1 0 1 2 3 …
y … -6 -4 -2 0 2 4 6 …
典例分析
如图所示,在直角坐标系中描出以表
中的值为坐标的点.将这些点连接起来,得到一条经
过原点和第三、第一象限的直线.它就是函数y=2x
的图象.
用同样的方法,可以得到
函数y= 的图象(如图).
它也是一条经过原点和第
三、第一象限的直线.
典例分析
如图,在直角坐标系中描出
以表中的值为坐标的点.将这
些点连接起来,得到一条经
过原点和第二、第四象限的
直线,它就是函数y=-1.5x
的图象.
用同样的方法,可以得到函数 y=-4x的图象(如
图). 它也是一条经过原点和第二、第四象限的直线.
典例分析
1.
用你认为最简单的方法画出下列函数的图象:
(1) (2) y=-3x.
解:函数y= x与函数y=-3x均
可以用两点法画图象,列表:
x 0 1
y= x 0
y=-3x 0 -3
描点连线,图象如图所示.
课堂练习
正比例函数的性质
2
在同一直角坐标系内画出正比例函数y=3x,
y=x, y= x的图象.
当k>0时,它的图像 经过第一、三象限.
1
y
x
o
3
3
1
自主学习
当k<0时,它的图像经过第二、四象限
在同一坐标系内画下列正比例函数的图像:
知识点
1
y
x
o
自主学习
自主学习
当k>0时,正比例函数的图像经过第一、三象限,
自变量x逐渐增大时,y的值也随着逐渐增大.
(2) 当k<0时,正比例函数的图像经过第二、四象限,
自变量x逐渐增大时,y的值则随着逐渐减小.
自主学习
x
y
0
1
1
当 |k| 越大时,
图像越靠近y轴
当 |k| 相等时,
图像关于坐标
轴对称
自主学习
例 3
〈珠海〉已知函数y=3x的图象经过点A(-1,y1),点B(-2,y2),则y1______y2(填“>”“<”或“=”).
导引:
方法一:把点A、点B的坐标分别代入函数
y=3x,求出y1,y2的值比较大小即可.
方法二:画出正比例函数y=3x的图象,在
函数图象上标出点A、点B,利用数形结合
思想来比较y1,y2的大小.如图,观察图形,
显然可得y1>y2.
>
典例分析
方法三:根据正比例函数的增减性来比较函数值的大小.
根据正比例函数的性质,当k>0时,y随x的增大而增大,
即可得y1>y2.
典例分析
归 纳
正比例函数图象上两点的纵坐标的大小与比例
系数及自变量的大小有关;比例系数是正数时,函
数值随自变量的增大而增大;比例系数是负数时,
函数值随自变量的增大而减小.本例的解法中,方
法一是利用求值比较法;方法二是利用数形结合思
想,用“形”上的点的位置来比较“数”的大小;
方法三是利用函数的增减性来比较大小.
典例分析
1.
已知正比例函数y=(k+5)x,且y随x的增大而减小,则k的取值范围是( )
A.k>5 B.k<5
C.k>-5 D.k<-5
D
课堂练习
2.
关于函数y=-2x,下列判断正确的是( )
A.图象经过第一、三象限
B.y随x的增大而增大
C.若(x1,y1),(x2,y2)是该函数图象上的两点,
则当x1
D.不论x为何值,总有y<0
C
课堂练习
3.
【中考·茂名】如图,三个正比例函数的图象分别对应解析式:①y=ax;②y=bx;③y=cx,将a,b,c从小到大排列并用“<”连接为___________.
a<c<b
课堂练习
4. 如图分别是函数y=k1 x,y=k2 x,y=k3 x,y=k4 x的图象.
(1)k1 k2,k3 k4(填“>”或“<”或“=”);
(2)用不等号将k1, k2, k3, k4及0依次连接起来.
<
解: k1<k2 <0<k3 <k4
4
2
-2
-4
4
x
y
O
y =k4 x
-4
-2
2
y =k3 x
y =k2 x
y =k1 x
<
课堂练习
正比例函数的
图象和性质
图象:正比例函数y=kx(k是常数,k≠0)的图象是
一条经过原点的直线,我们称它为直线y=kx.
性质:
当k>0时,直线y=kx经过第一、三象限,从
左向右上升,y随着x的增大而增大;
当k<0时,直线y=kx经过第二、四象限,从
左向右下降,y随着x的增大而减小.
https://www.21cnjy.com/help/help_extract.php
