沪教版九年级数学上册二次函数单元测试一
文档属性
| 名称 | 沪教版九年级数学上册二次函数单元测试一 |
|
|
| 格式 | zip | ||
| 文件大小 | 124.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-14 08:42:53 | ||
图片预览




文档简介
沪教版九年级数学上册二次函数单元测试一
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.已知二次函数(a<0)的图象经过点A(-2,0)、O(0,0)、B(-3,y1)、C(3,y2)四点,则y1与y2的大小关系正确的是( )
A. y1<y2 B. y1>y2 C. y1=y2 D.不能确定
2.下列二次函数中,图象以直线x = 2为对称轴,且经过点(0,1)的是( )
A.y = (x ? 2)2 + 1 B.y = (x + 2)2 + 1
C.y = (x ? 2)2 ? 3 D.y = (x + 2)2 – 3
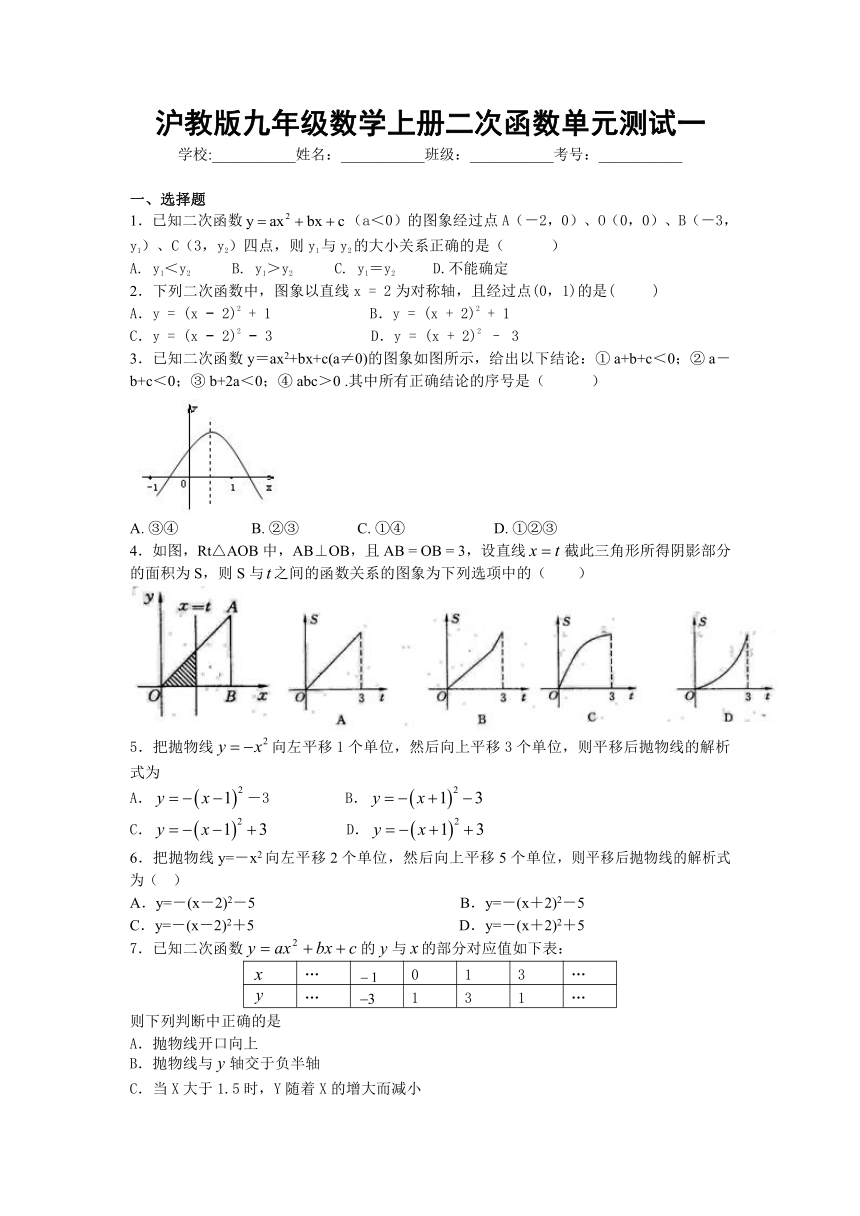
3.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:① a+b+c<0;② a-b+c<0;③ b+2a<0;④ abc>0 .其中所有正确结论的序号是( )
A. ③④ B. ②③ C. ①④ D. ①②③
4.如图,Rt△AOB中,AB⊥OB,且AB = OB = 3,设直线截此三角形所得阴影部分的面积为S,则S与之间的函数关系的图象为下列选项中的( )
5.把抛物线向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为
A.-3 B.
C. D.
6.把抛物线y=-x2向左平移2个单位,然后向上平移5个单位,则平移后抛物线的解析式为( )
A.y=-(x-2)2-5 B.y=-(x+2)2-5
C.y=-(x-2)2+5 D.y=-(x+2)2+5
7.已知二次函数的与的部分对应值如下表:
…
0
1
3
…
…
1
3
1
…
则下列判断中正确的是
A.抛物线开口向上
B.抛物线与轴交于负半轴
C.当X大于1.5时,Y随着X的增大而减小
D.当=4时,>0
8.已知抛物线,当自变量取两个不同的数值 时,函数值相等,则当自变量取时的函数值与( )
A. 时,函数值相等 B. 时,函数值相等
C. 时,函数值相等 D. 时,函数值相等
9.如图,矩形在平面直角坐标系中的位置如图所示,,.抛物线()经过点和点,与轴分别交于点、(点在点左侧),且,则下列结论:①;②;③;④;⑤连接、,则,其中正确结论的个数为
A.个 B.个 C.个 D.个
10.定义符号表示与自变量所对应的函数值。例如对于函数,当时,对应的函数值,则可以写为:。在二次函数中,若对任意实数都成立,那么下列结论错误的是( )
二、填空题
11.若抛物线y=ax2+bx+c的顶点是A(2,1),且经过点B(1,0),则抛物线的函数关系式为 .
12.若抛物线经过坐标原点,则这个抛物线的顶点坐标是
13.抛物线的顶点坐标是 .
14.将抛物线y1=2x2向右平移2个单位,得到抛物线y2的图象,则y2= ;
15.将抛物线向下平移2个单位再向右平移3个单位,所得抛物线的表达式是 .
16.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
从上表可知,下列说法中正确的有______ .(填写序号)
①抛物线与x轴的一个交点为(3,0);
②函数y=ax2+bx+c的最大值为6;
③抛物线的对称轴是x=;
④在对称轴左侧,y随x的增大而增大.
17.已知恒成立,那么实数x的取值范围是
18.如图,已知抛物线,与轴交于A、B两点,点为抛物线的顶点。点P在抛物线的对称轴上,设⊙P的半径为,当⊙P与轴和直线BC都相切时,则圆心P的坐标为 .
三、计算题
如图所示,已知平面直角坐标系xOy,抛物线过点A(4,0)、B(1,3)
19.求该抛物线的表达式,并写出该抛物线的对称轴和顶点坐标;
20.记该抛物线的对称轴为直线l,设抛物线上的点P(m,n)在第四象限,点P关于直线l的对称点为E,点E关于y轴的对称点为F,若四边形OAPF的面积为20,求m、n的值.
设函数y=kx2+(2k+1)x+1(k为实数).
21.写出其中的两个特殊函数,使它们的图象不全是抛物线,并在同一直角坐标系中用描点法画出这两个特殊函数的图象
22.根据所画图象,猜想出:对任意实数k,函数的图象都具有的特征,并给予证明
23.对任意负实数k,当x四、解答题
24.在直角坐标系中,已知抛物线与x轴交于点A(1,0)和点B,顶点为P.
(1)若点P的坐标为(-1,4),求此时抛物线的解析式;
(2)如图若点P的坐标为(-1,k),k<0,点Q是y轴上一个动点,
当k为何值时,QB+QP取得最小值为5;
(3)试求满足(2)时动点Q的坐标. (本题12分)
25.年初,中共中央国务院发布了1号文件,为了落实关于惠农的文件精神,江苏省出台
了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农副产品,已知这种产
品的成本价为20元/千克.市场调查发现,该产品每天的销售量w(千克)与销售价x(元/千克)有如
下关系:w=-2x+80.设这种产品每天的销售利润为y(元) .
(1)求y与x之间的函数关系式;
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果物价部门规定这种产品的销售价不得高于28元/千克,该农户想要每天获得150元的销售利润,销售价应定为多少元?
26.某批发商以每件50元的价格购进800件T恤.第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓,清仓时单价为40元.设第二个月单价降低元.
(1)填表:
时间
第一个月
第二个月
清仓
单价(元)
80
40
销售量(件)
200
(2)如果批发商希望通过销售这批T恤获利9 000元,那么第二个月的单价应是多少元?
27.把一边长为60cm的正方形硬纸板,进行适当的剪裁,折成一个长方体盒子(纸板的厚度忽略不计).
(1)如图1,若在正方形硬纸板的四角各剪一个同样大小的正方形,将剩余部分折成一个无盖的长方体盒子.
①要使折成的长方体盒子的底面积为576cm2,那么剪掉的正方形的边长为多少?
②折成的长方体盒子的侧面积是否有最大值?如果有,求出这个最大值和此时剪掉的正方形的边长;如果没有,说明理由.
(2)如图2,若在正方形硬纸板的四周剪掉一些矩形(即剪掉的矩形至少有一条边在正方形硬纸板的边上),将剩余部分正好折成一个有盖的长方体盒子.若折成的一个长方体盒子的表面积为2800cm2,求此时长方体盒子的长、宽、高(只需求出符合要求的一种情况).
28.用一段长为30米的篱笆围成一个一边靠墙的矩形菜园,墙长为18米,这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
参考答案
1.B
2.C
3.B
4.D
5.D
6.D
7.C
8.B
9.C
10.C
11.y=-(x-2)2+1
12.(0,0)
13.(1,2)
14.
15.
16.①③④
17.
18.,
19.y=-,
对称轴为:x=2,顶点坐标为:(2,4)
20.m、n的值分别为 5,-5
21.当k=1时,y= x2+3x+1;当k=0时y=x+1, 图象略
22.见解析
23.只要m的值不大于-1即可
24.;k=-3;Q点的坐标为(0,)
25.(1) ……………4分
(2)当销售价定为30元时,每天的销售利润最大,最大利润是200元.………7分
(3)销售价应定为25元
26.(1);;;(2)70元
27.(1)①剪掉的正方形的边长为18cm。 ……3分
②侧面积有最大值。
当剪掉的正方形的边长为15cm时,长方形盒子的侧面积最大为1800cm2。
(2)剪掉的正方形的边长为10cm。
此时长方体盒子的长为40cm,宽为20cm,高为10cm。……10分
28.当矩形的长为15m,宽为7.5m时,矩形菜园的面积最大,最大面积为112.5米2
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.已知二次函数(a<0)的图象经过点A(-2,0)、O(0,0)、B(-3,y1)、C(3,y2)四点,则y1与y2的大小关系正确的是( )
A. y1<y2 B. y1>y2 C. y1=y2 D.不能确定
2.下列二次函数中,图象以直线x = 2为对称轴,且经过点(0,1)的是( )
A.y = (x ? 2)2 + 1 B.y = (x + 2)2 + 1
C.y = (x ? 2)2 ? 3 D.y = (x + 2)2 – 3
3.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:① a+b+c<0;② a-b+c<0;③ b+2a<0;④ abc>0 .其中所有正确结论的序号是( )
A. ③④ B. ②③ C. ①④ D. ①②③
4.如图,Rt△AOB中,AB⊥OB,且AB = OB = 3,设直线截此三角形所得阴影部分的面积为S,则S与之间的函数关系的图象为下列选项中的( )
5.把抛物线向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为
A.-3 B.
C. D.
6.把抛物线y=-x2向左平移2个单位,然后向上平移5个单位,则平移后抛物线的解析式为( )
A.y=-(x-2)2-5 B.y=-(x+2)2-5
C.y=-(x-2)2+5 D.y=-(x+2)2+5
7.已知二次函数的与的部分对应值如下表:
…
0
1
3
…
…
1
3
1
…
则下列判断中正确的是
A.抛物线开口向上
B.抛物线与轴交于负半轴
C.当X大于1.5时,Y随着X的增大而减小
D.当=4时,>0
8.已知抛物线,当自变量取两个不同的数值 时,函数值相等,则当自变量取时的函数值与( )
A. 时,函数值相等 B. 时,函数值相等
C. 时,函数值相等 D. 时,函数值相等
9.如图,矩形在平面直角坐标系中的位置如图所示,,.抛物线()经过点和点,与轴分别交于点、(点在点左侧),且,则下列结论:①;②;③;④;⑤连接、,则,其中正确结论的个数为
A.个 B.个 C.个 D.个
10.定义符号表示与自变量所对应的函数值。例如对于函数,当时,对应的函数值,则可以写为:。在二次函数中,若对任意实数都成立,那么下列结论错误的是( )
二、填空题
11.若抛物线y=ax2+bx+c的顶点是A(2,1),且经过点B(1,0),则抛物线的函数关系式为 .
12.若抛物线经过坐标原点,则这个抛物线的顶点坐标是
13.抛物线的顶点坐标是 .
14.将抛物线y1=2x2向右平移2个单位,得到抛物线y2的图象,则y2= ;
15.将抛物线向下平移2个单位再向右平移3个单位,所得抛物线的表达式是 .
16.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
从上表可知,下列说法中正确的有______ .(填写序号)
①抛物线与x轴的一个交点为(3,0);
②函数y=ax2+bx+c的最大值为6;
③抛物线的对称轴是x=;
④在对称轴左侧,y随x的增大而增大.
17.已知恒成立,那么实数x的取值范围是
18.如图,已知抛物线,与轴交于A、B两点,点为抛物线的顶点。点P在抛物线的对称轴上,设⊙P的半径为,当⊙P与轴和直线BC都相切时,则圆心P的坐标为 .
三、计算题
如图所示,已知平面直角坐标系xOy,抛物线过点A(4,0)、B(1,3)
19.求该抛物线的表达式,并写出该抛物线的对称轴和顶点坐标;
20.记该抛物线的对称轴为直线l,设抛物线上的点P(m,n)在第四象限,点P关于直线l的对称点为E,点E关于y轴的对称点为F,若四边形OAPF的面积为20,求m、n的值.
设函数y=kx2+(2k+1)x+1(k为实数).
21.写出其中的两个特殊函数,使它们的图象不全是抛物线,并在同一直角坐标系中用描点法画出这两个特殊函数的图象
22.根据所画图象,猜想出:对任意实数k,函数的图象都具有的特征,并给予证明
23.对任意负实数k,当x
24.在直角坐标系中,已知抛物线与x轴交于点A(1,0)和点B,顶点为P.
(1)若点P的坐标为(-1,4),求此时抛物线的解析式;
(2)如图若点P的坐标为(-1,k),k<0,点Q是y轴上一个动点,
当k为何值时,QB+QP取得最小值为5;
(3)试求满足(2)时动点Q的坐标. (本题12分)
25.年初,中共中央国务院发布了1号文件,为了落实关于惠农的文件精神,江苏省出台
了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农副产品,已知这种产
品的成本价为20元/千克.市场调查发现,该产品每天的销售量w(千克)与销售价x(元/千克)有如
下关系:w=-2x+80.设这种产品每天的销售利润为y(元) .
(1)求y与x之间的函数关系式;
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果物价部门规定这种产品的销售价不得高于28元/千克,该农户想要每天获得150元的销售利润,销售价应定为多少元?
26.某批发商以每件50元的价格购进800件T恤.第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓,清仓时单价为40元.设第二个月单价降低元.
(1)填表:
时间
第一个月
第二个月
清仓
单价(元)
80
40
销售量(件)
200
(2)如果批发商希望通过销售这批T恤获利9 000元,那么第二个月的单价应是多少元?
27.把一边长为60cm的正方形硬纸板,进行适当的剪裁,折成一个长方体盒子(纸板的厚度忽略不计).
(1)如图1,若在正方形硬纸板的四角各剪一个同样大小的正方形,将剩余部分折成一个无盖的长方体盒子.
①要使折成的长方体盒子的底面积为576cm2,那么剪掉的正方形的边长为多少?
②折成的长方体盒子的侧面积是否有最大值?如果有,求出这个最大值和此时剪掉的正方形的边长;如果没有,说明理由.
(2)如图2,若在正方形硬纸板的四周剪掉一些矩形(即剪掉的矩形至少有一条边在正方形硬纸板的边上),将剩余部分正好折成一个有盖的长方体盒子.若折成的一个长方体盒子的表面积为2800cm2,求此时长方体盒子的长、宽、高(只需求出符合要求的一种情况).
28.用一段长为30米的篱笆围成一个一边靠墙的矩形菜园,墙长为18米,这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
参考答案
1.B
2.C
3.B
4.D
5.D
6.D
7.C
8.B
9.C
10.C
11.y=-(x-2)2+1
12.(0,0)
13.(1,2)
14.
15.
16.①③④
17.
18.,
19.y=-,
对称轴为:x=2,顶点坐标为:(2,4)
20.m、n的值分别为 5,-5
21.当k=1时,y= x2+3x+1;当k=0时y=x+1, 图象略
22.见解析
23.只要m的值不大于-1即可
24.;k=-3;Q点的坐标为(0,)
25.(1) ……………4分
(2)当销售价定为30元时,每天的销售利润最大,最大利润是200元.………7分
(3)销售价应定为25元
26.(1);;;(2)70元
27.(1)①剪掉的正方形的边长为18cm。 ……3分
②侧面积有最大值。
当剪掉的正方形的边长为15cm时,长方形盒子的侧面积最大为1800cm2。
(2)剪掉的正方形的边长为10cm。
此时长方体盒子的长为40cm,宽为20cm,高为10cm。……10分
28.当矩形的长为15m,宽为7.5m时,矩形菜园的面积最大,最大面积为112.5米2
