二次函数y=ax2的图像和性质
图片预览





文档简介
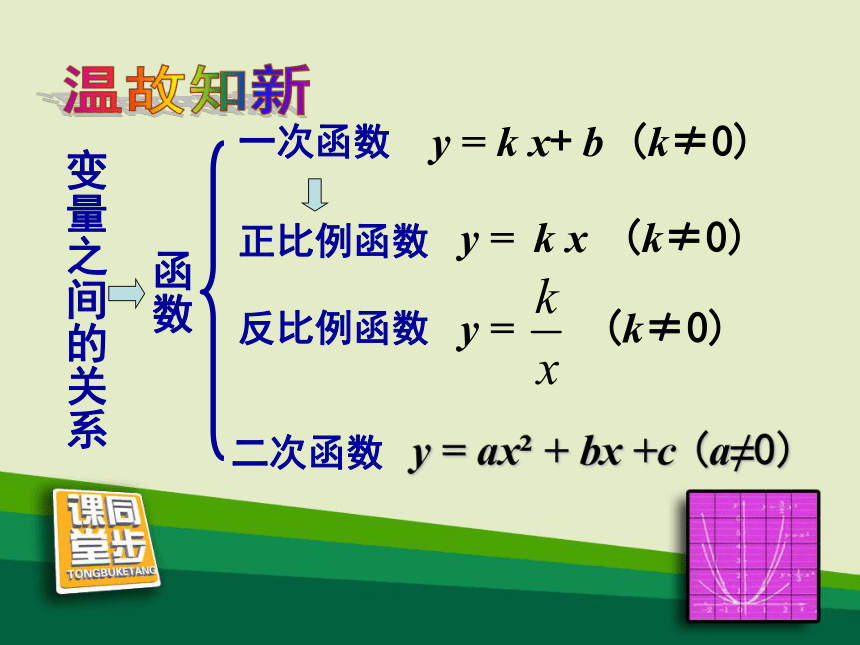
课件34张PPT。c是常数,a≠0)1.一般地,形如2.我们学习过哪些函数?y =a x2 + b x + c (a、b、的函数叫做 x 的二次函数.温故知新y = ax2 + bx +c (a≠0)二次函数y = k x+ b (k≠0)y = k x (k≠0)一次函数变量之间的关系函数反比例函数正比例函数温故知新
3.一次函数的图象是 .
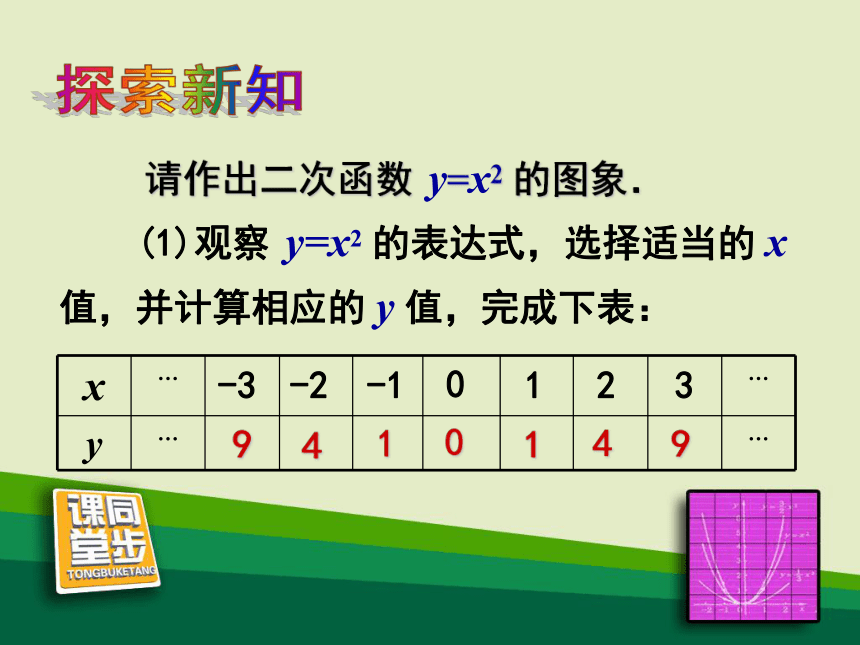
4.反比例函数的图象是 .双曲线5.二次函数的图象是什么形状呢?温故知新一条直线(3)连线. (1)列表;用描点法画函数图象的主要步骤是:(2)描点; 6.通常怎样画一个函数的图象?答:通常用描点法画一个函数的图象.温故知新 (1)观察 y=x2 的表达式,选择适当的 x 值,并计算相应的 y 值,完成下表:
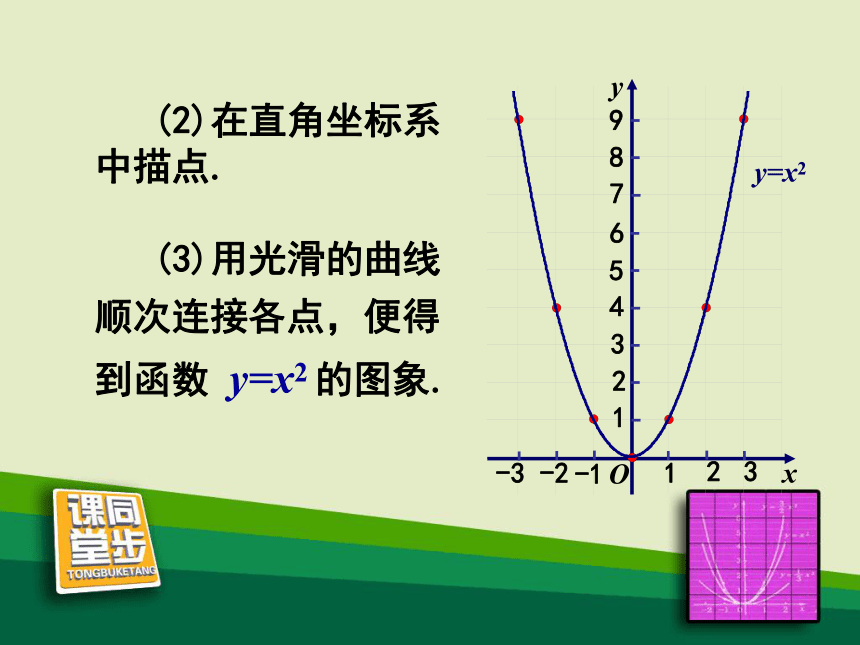
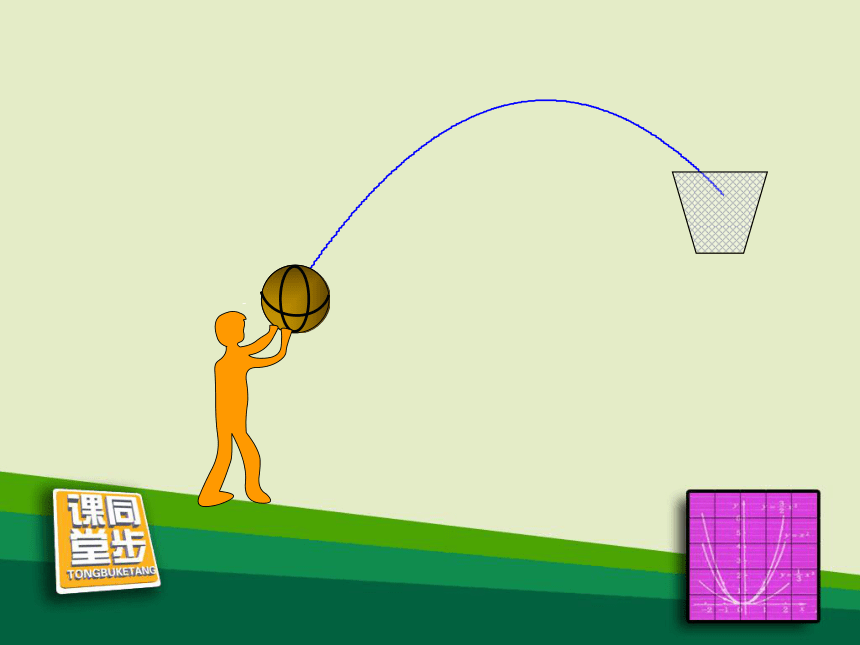
请作出二次函数 y=x2 的图象.-3-2-10123探索新知 (2)在直角坐标系中描点. (3)用光滑的曲线顺次连接各点,便得到函数 y=x2 的图象. y=x2二次函数y=ax2的图象形如物体抛射时
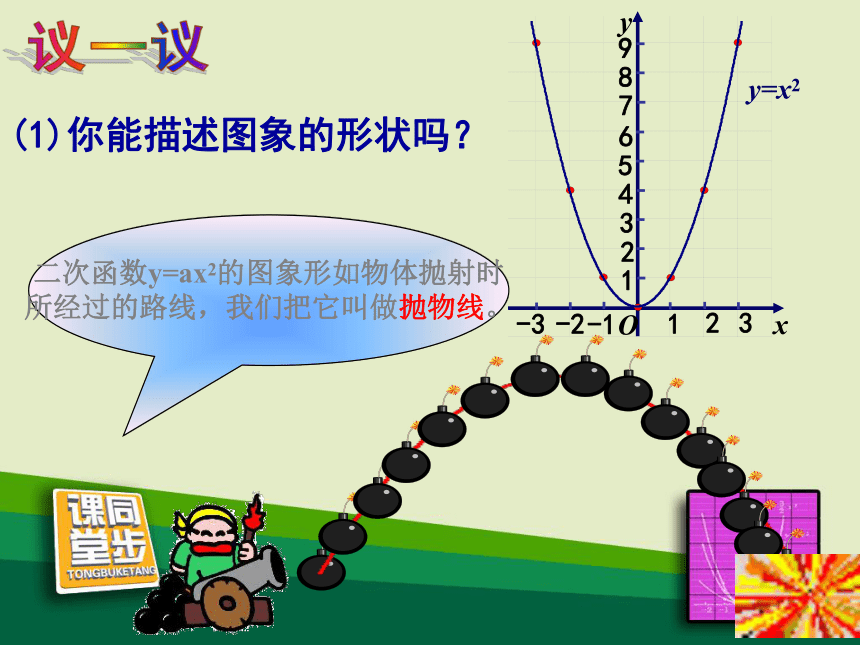
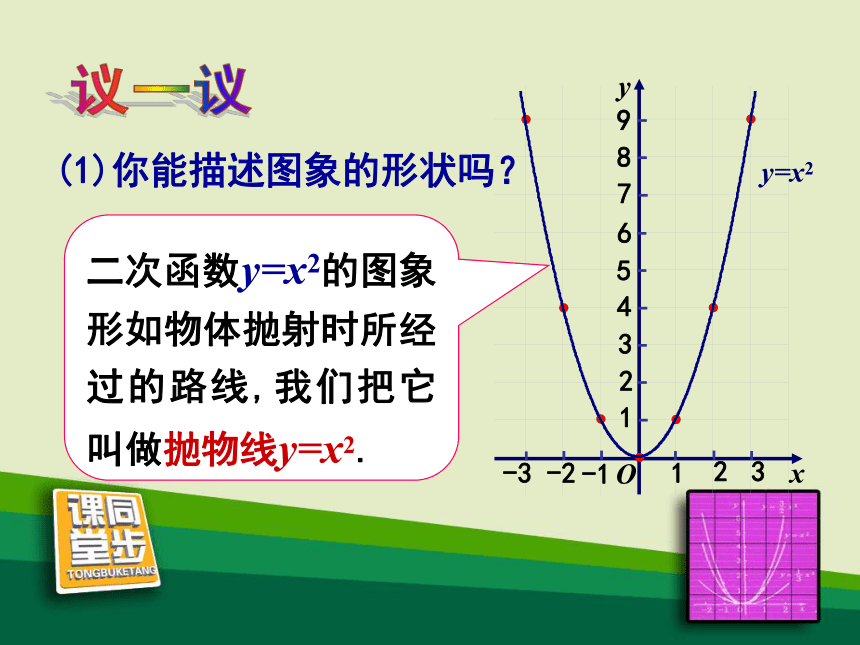
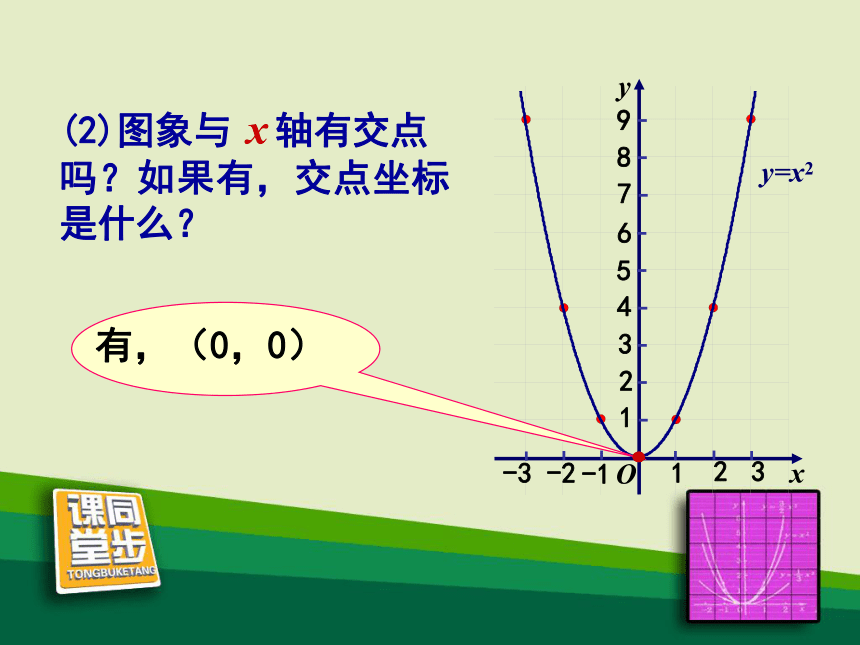
所经过的路线,我们把它叫做抛物线。议一议(1)你能描述图象的形状吗?(1)你能描述图象的形状吗?议一议二次函数y=x2的图象形如物体抛射时所经过的路线,我们把它叫做抛物线y=x2.(2)图象与 x 轴有交点 吗?如果有,交点坐标是什么?有,(0,0)(3)当x<0时,随着x值的增大, y的值如何变化?当x>0时呢?当 x<0 时,y随着x的增大而减小.当 x>0 时,y随着x的增大而增大.(4)当x取什么值时,y的值最小?最小值是什么?你是如何知道的? 当 x=0 时,函数 y 的值最小,最小值是0. 可以观察图象,也可以分析表达式. 是,对称轴是 y 轴.(-2,4)和(2,4);(-3,9)和(3,9)等等.(-1,1)和(1,1);(5)图象是轴对称图形吗?如果是,它的对称轴是什么?请你找出几对对称点.对称点有很多,如: 二次函数y=x2的图象的顶点是原点,它是图象的最低点.(6)图象与对称轴有交点吗? 二次函数 y=x2 的图象是一条抛物线,它的特点是:1.开口向上;2.对称轴是y轴; 3.顶点是原点,它是图象的最低点.作出二次函数 y = -x2 的图象.(1) 列表: (2)在直角坐标系中描点. (3)用光滑的曲线顺次连接各点,便得到函数 y=-x2 的图象. y=- x2(1)二次函数 y=-x2 的图象是一条抛物线.(2)图象与 x 轴交于原点(0,0). 二次函数 y=-x2 的图象是一条抛物线,它的特点是:1.开口向下;2.对称轴是y轴; 3.顶点是原点,它是图象的最高点.2.顶点坐标;1.对称轴; 3.开口方向;二次函数 y=±x2 的图象和性质:4.增减性;5.最值.yy=x2y=-x2在对称轴左侧,y随x的增大而增大;在对称轴右侧,y随着x的增大而减小y 轴开口向上开口向下y 轴原点(最低点)原点(最高点)当x=0时,最大值为0在对称轴左侧,y随x的增大而减小;在对称轴右
侧,y随着x的增大而增大当x=0时,最小值为0相同点:归纳3.形状完全相同.
1.顶点都是原点;2.对称轴都是 y 轴;二次函数 y=±x2 的图象和性质:不同点:1.开口方向不同; 2.y 随 x 值的变化趋势不同;3.最值不同.
实际上,二次函数的图象都是抛物线,它们的开口或者向上或者向下.一般地,二次函数 y =a x2 + b x + c 的图象叫做抛物线 y =a x2 + b x + c .
每条抛物线都有对称轴,顶点是抛物线的最低点或最高点.随堂练习2.点 A(2,a),B(b,9)在抛物线 y=x2 上,则 a = ,b = . 4±31.抛物线 y=ax2 与 y=x2 的开口大小、形状一样、开口方向相反,则 a = .-14.二次函数 y = -x2 的图象,在 y 轴的右边,y 随 x 的增大而________.减小3.若点 A(2,m)在抛物线 y=x2 上,则点A关于 y 轴对称点的坐标是 .(-2,4)随堂练习5.已知 a<-1,点(a-1,y1)、(a,y2)、(a+1,y3)都在函数 y=x2 的图象上,则(????? )
A.y1<y2<y3 B.y1<y3<y2?????
C.y3<y2<y1 D.y2<y1<y3C观察图象,在 y 轴的左侧 y 随 x 的增大而减小,所以 y3<y2<y1.y1y2y3也可以用特殊值法计算得到答案.分析:用数形结合的思想解决问题.6.设正方形的边长为 a,面积为 S,试作出 S 随 a 的变化而变化的图象.解:S = a2(a>0)列表:0149描点并连线.S=a2 此外,二次函数在建筑学上也有重要应用,如抛物线型隧道、抛物线型拱桥、抛物线型吊桥、抛物线型弯道等.要确定这些抛物线的形状,需要对地质、地形、气象、水力、材料等因素进行综合分析.二次函数的广泛应用课件34张PPT。c是常数,a≠0)1.一般地,形如2.我们学习过哪些函数?y =a x2 + b x + c (a、b、的函数叫做 x 的二次函数.温故知新y = ax2 + bx +c (a≠0)二次函数y = k x+ b (k≠0)y = k x (k≠0)一次函数变量之间的关系函数反比例函数正比例函数y = (k≠0)
温故知新
3.一次函数的图象是 .
4.反比例函数的图象是 .双曲线5.二次函数的图象是什么形状呢?温故知新一条直线(3)连线. (1)列表;用描点法画函数图象的主要步骤是:(2)描点; 6.通常怎样画一个函数的图象?答:通常用描点法画一个函数的图象.温故知新 (1)观察 y=x2 的表达式,选择适当的 x 值,并计算相应的 y 值,完成下表:
请作出二次函数 y=x2 的图象.-3-2-10123探索新知 (2)在直角坐标系中描点. (3)用光滑的曲线顺次连接各点,便得到函数 y=x2 的图象. y=x2二次函数y=ax2的图象形如物体抛射时
所经过的路线,我们把它叫做抛物线。议一议(1)你能描述图象的形状吗?(1)你能描述图象的形状吗?议一议二次函数y=x2的图象形如物体抛射时所经过的路线,我们把它叫做抛物线y=x2.(2)图象与 x 轴有交点 吗?如果有,交点坐标是什么?有,(0,0)(3)当x<0时,随着x值的增大, y的值如何变化?当x>0时呢?当 x<0 时,y随着x的增大而减小.当 x>0 时,y随着x的增大而增大.(4)当x取什么值时,y的值最小?最小值是什么?你是如何知道的? 当 x=0 时,函数 y 的值最小,最小值是0. 可以观察图象,也可以分析表达式. 是,对称轴是 y 轴.(-2,4)和(2,4);(-3,9)和(3,9)等等.(-1,1)和(1,1);(5)图象是轴对称图形吗?如果是,它的对称轴是什么?请你找出几对对称点.对称点有很多,如: 二次函数y=x2的图象的顶点是原点,它是图象的最低点.(6)图象与对称轴有交点吗? 二次函数 y=x2 的图象是一条抛物线,它的特点是:1.开口向上;2.对称轴是y轴; 3.顶点是原点,它是图象的最低点.作出二次函数 y = -x2 的图象.(1) 列表: (2)在直角坐标系中描点. (3)用光滑的曲线顺次连接各点,便得到函数 y=-x2 的图象. y=- x2(1)二次函数 y=-x2 的图象是一条抛物线.(2)图象与 x 轴交于原点(0,0). 二次函数 y=-x2 的图象是一条抛物线,它的特点是:1.开口向下;2.对称轴是y轴; 3.顶点是原点,它是图象的最高点.2.顶点坐标;1.对称轴; 3.开口方向;二次函数 y=±x2 的图象和性质:4.增减性;5.最值.yy=x2y=-x2在对称轴左侧,y随x的增大而增大;在对称轴右侧,y随着x的增大而减小y 轴开口向上开口向下y 轴原点(最低点)原点(最高点)当x=0时,最大值为0在对称轴左侧,y随x的增大而减小;在对称轴右
侧,y随着x的增大而增大当x=0时,最小值为0相同点:归纳3.形状完全相同.
1.顶点都是原点;2.对称轴都是 y 轴;二次函数 y=±x2 的图象和性质:不同点:1.开口方向不同; 2.y 随 x 值的变化趋势不同;3.最值不同.
实际上,二次函数的图象都是抛物线,它们的开口或者向上或者向下.一般地,二次函数 y =a x2 + b x + c 的图象叫做抛物线 y =a x2 + b x + c .
每条抛物线都有对称轴,顶点是抛物线的最低点或最高点.随堂练习2.点 A(2,a),B(b,9)在抛物线 y=x2 上,则 a = ,b = . 4±31.抛物线 y=ax2 与 y=x2 的开口大小、形状一样、开口方向相反,则 a = .-14.二次函数 y = -x2 的图象,在 y 轴的右边,y 随 x 的增大而________.减小3.若点 A(2,m)在抛物线 y=x2 上,则点A关于 y 轴对称点的坐标是 .(-2,4)随堂练习5.已知 a<-1,点(a-1,y1)、(a,y2)、(a+1,y3)都在函数 y=x2 的图象上,则(????? )
A.y1<y2<y3 B.y1<y3<y2?????
C.y3<y2<y1 D.y2<y1<y3C观察图象,在 y 轴的左侧 y 随 x 的增大而减小,所以 y3<y2<y1.y1y2y3也可以用特殊值法计算得到答案.分析:用数形结合的思想解决问题.6.设正方形的边长为 a,面积为 S,试作出 S 随 a 的变化而变化的图象.解:S = a2(a>0)列表:0149描点并连线.S=a2 此外,二次函数在建筑学上也有重要应用,如抛物线型隧道、抛物线型拱桥、抛物线型吊桥、抛物线型弯道等.要确定这些抛物线的形状,需要对地质、地形、气象、水力、材料等因素进行综合分析.二次函数的广泛应用
3.一次函数的图象是 .
4.反比例函数的图象是 .双曲线5.二次函数的图象是什么形状呢?温故知新一条直线(3)连线. (1)列表;用描点法画函数图象的主要步骤是:(2)描点; 6.通常怎样画一个函数的图象?答:通常用描点法画一个函数的图象.温故知新 (1)观察 y=x2 的表达式,选择适当的 x 值,并计算相应的 y 值,完成下表:
请作出二次函数 y=x2 的图象.-3-2-10123探索新知 (2)在直角坐标系中描点. (3)用光滑的曲线顺次连接各点,便得到函数 y=x2 的图象. y=x2二次函数y=ax2的图象形如物体抛射时
所经过的路线,我们把它叫做抛物线。议一议(1)你能描述图象的形状吗?(1)你能描述图象的形状吗?议一议二次函数y=x2的图象形如物体抛射时所经过的路线,我们把它叫做抛物线y=x2.(2)图象与 x 轴有交点 吗?如果有,交点坐标是什么?有,(0,0)(3)当x<0时,随着x值的增大, y的值如何变化?当x>0时呢?当 x<0 时,y随着x的增大而减小.当 x>0 时,y随着x的增大而增大.(4)当x取什么值时,y的值最小?最小值是什么?你是如何知道的? 当 x=0 时,函数 y 的值最小,最小值是0. 可以观察图象,也可以分析表达式. 是,对称轴是 y 轴.(-2,4)和(2,4);(-3,9)和(3,9)等等.(-1,1)和(1,1);(5)图象是轴对称图形吗?如果是,它的对称轴是什么?请你找出几对对称点.对称点有很多,如: 二次函数y=x2的图象的顶点是原点,它是图象的最低点.(6)图象与对称轴有交点吗? 二次函数 y=x2 的图象是一条抛物线,它的特点是:1.开口向上;2.对称轴是y轴; 3.顶点是原点,它是图象的最低点.作出二次函数 y = -x2 的图象.(1) 列表: (2)在直角坐标系中描点. (3)用光滑的曲线顺次连接各点,便得到函数 y=-x2 的图象. y=- x2(1)二次函数 y=-x2 的图象是一条抛物线.(2)图象与 x 轴交于原点(0,0). 二次函数 y=-x2 的图象是一条抛物线,它的特点是:1.开口向下;2.对称轴是y轴; 3.顶点是原点,它是图象的最高点.2.顶点坐标;1.对称轴; 3.开口方向;二次函数 y=±x2 的图象和性质:4.增减性;5.最值.yy=x2y=-x2在对称轴左侧,y随x的增大而增大;在对称轴右侧,y随着x的增大而减小y 轴开口向上开口向下y 轴原点(最低点)原点(最高点)当x=0时,最大值为0在对称轴左侧,y随x的增大而减小;在对称轴右
侧,y随着x的增大而增大当x=0时,最小值为0相同点:归纳3.形状完全相同.
1.顶点都是原点;2.对称轴都是 y 轴;二次函数 y=±x2 的图象和性质:不同点:1.开口方向不同; 2.y 随 x 值的变化趋势不同;3.最值不同.
实际上,二次函数的图象都是抛物线,它们的开口或者向上或者向下.一般地,二次函数 y =a x2 + b x + c 的图象叫做抛物线 y =a x2 + b x + c .
每条抛物线都有对称轴,顶点是抛物线的最低点或最高点.随堂练习2.点 A(2,a),B(b,9)在抛物线 y=x2 上,则 a = ,b = . 4±31.抛物线 y=ax2 与 y=x2 的开口大小、形状一样、开口方向相反,则 a = .-14.二次函数 y = -x2 的图象,在 y 轴的右边,y 随 x 的增大而________.减小3.若点 A(2,m)在抛物线 y=x2 上,则点A关于 y 轴对称点的坐标是 .(-2,4)随堂练习5.已知 a<-1,点(a-1,y1)、(a,y2)、(a+1,y3)都在函数 y=x2 的图象上,则(????? )
A.y1<y2<y3 B.y1<y3<y2?????
C.y3<y2<y1 D.y2<y1<y3C观察图象,在 y 轴的左侧 y 随 x 的增大而减小,所以 y3<y2<y1.y1y2y3也可以用特殊值法计算得到答案.分析:用数形结合的思想解决问题.6.设正方形的边长为 a,面积为 S,试作出 S 随 a 的变化而变化的图象.解:S = a2(a>0)列表:0149描点并连线.S=a2 此外,二次函数在建筑学上也有重要应用,如抛物线型隧道、抛物线型拱桥、抛物线型吊桥、抛物线型弯道等.要确定这些抛物线的形状,需要对地质、地形、气象、水力、材料等因素进行综合分析.二次函数的广泛应用课件34张PPT。c是常数,a≠0)1.一般地,形如2.我们学习过哪些函数?y =a x2 + b x + c (a、b、的函数叫做 x 的二次函数.温故知新y = ax2 + bx +c (a≠0)二次函数y = k x+ b (k≠0)y = k x (k≠0)一次函数变量之间的关系函数反比例函数正比例函数y = (k≠0)
温故知新
3.一次函数的图象是 .
4.反比例函数的图象是 .双曲线5.二次函数的图象是什么形状呢?温故知新一条直线(3)连线. (1)列表;用描点法画函数图象的主要步骤是:(2)描点; 6.通常怎样画一个函数的图象?答:通常用描点法画一个函数的图象.温故知新 (1)观察 y=x2 的表达式,选择适当的 x 值,并计算相应的 y 值,完成下表:
请作出二次函数 y=x2 的图象.-3-2-10123探索新知 (2)在直角坐标系中描点. (3)用光滑的曲线顺次连接各点,便得到函数 y=x2 的图象. y=x2二次函数y=ax2的图象形如物体抛射时
所经过的路线,我们把它叫做抛物线。议一议(1)你能描述图象的形状吗?(1)你能描述图象的形状吗?议一议二次函数y=x2的图象形如物体抛射时所经过的路线,我们把它叫做抛物线y=x2.(2)图象与 x 轴有交点 吗?如果有,交点坐标是什么?有,(0,0)(3)当x<0时,随着x值的增大, y的值如何变化?当x>0时呢?当 x<0 时,y随着x的增大而减小.当 x>0 时,y随着x的增大而增大.(4)当x取什么值时,y的值最小?最小值是什么?你是如何知道的? 当 x=0 时,函数 y 的值最小,最小值是0. 可以观察图象,也可以分析表达式. 是,对称轴是 y 轴.(-2,4)和(2,4);(-3,9)和(3,9)等等.(-1,1)和(1,1);(5)图象是轴对称图形吗?如果是,它的对称轴是什么?请你找出几对对称点.对称点有很多,如: 二次函数y=x2的图象的顶点是原点,它是图象的最低点.(6)图象与对称轴有交点吗? 二次函数 y=x2 的图象是一条抛物线,它的特点是:1.开口向上;2.对称轴是y轴; 3.顶点是原点,它是图象的最低点.作出二次函数 y = -x2 的图象.(1) 列表: (2)在直角坐标系中描点. (3)用光滑的曲线顺次连接各点,便得到函数 y=-x2 的图象. y=- x2(1)二次函数 y=-x2 的图象是一条抛物线.(2)图象与 x 轴交于原点(0,0). 二次函数 y=-x2 的图象是一条抛物线,它的特点是:1.开口向下;2.对称轴是y轴; 3.顶点是原点,它是图象的最高点.2.顶点坐标;1.对称轴; 3.开口方向;二次函数 y=±x2 的图象和性质:4.增减性;5.最值.yy=x2y=-x2在对称轴左侧,y随x的增大而增大;在对称轴右侧,y随着x的增大而减小y 轴开口向上开口向下y 轴原点(最低点)原点(最高点)当x=0时,最大值为0在对称轴左侧,y随x的增大而减小;在对称轴右
侧,y随着x的增大而增大当x=0时,最小值为0相同点:归纳3.形状完全相同.
1.顶点都是原点;2.对称轴都是 y 轴;二次函数 y=±x2 的图象和性质:不同点:1.开口方向不同; 2.y 随 x 值的变化趋势不同;3.最值不同.
实际上,二次函数的图象都是抛物线,它们的开口或者向上或者向下.一般地,二次函数 y =a x2 + b x + c 的图象叫做抛物线 y =a x2 + b x + c .
每条抛物线都有对称轴,顶点是抛物线的最低点或最高点.随堂练习2.点 A(2,a),B(b,9)在抛物线 y=x2 上,则 a = ,b = . 4±31.抛物线 y=ax2 与 y=x2 的开口大小、形状一样、开口方向相反,则 a = .-14.二次函数 y = -x2 的图象,在 y 轴的右边,y 随 x 的增大而________.减小3.若点 A(2,m)在抛物线 y=x2 上,则点A关于 y 轴对称点的坐标是 .(-2,4)随堂练习5.已知 a<-1,点(a-1,y1)、(a,y2)、(a+1,y3)都在函数 y=x2 的图象上,则(????? )
A.y1<y2<y3 B.y1<y3<y2?????
C.y3<y2<y1 D.y2<y1<y3C观察图象,在 y 轴的左侧 y 随 x 的增大而减小,所以 y3<y2<y1.y1y2y3也可以用特殊值法计算得到答案.分析:用数形结合的思想解决问题.6.设正方形的边长为 a,面积为 S,试作出 S 随 a 的变化而变化的图象.解:S = a2(a>0)列表:0149描点并连线.S=a2 此外,二次函数在建筑学上也有重要应用,如抛物线型隧道、抛物线型拱桥、抛物线型吊桥、抛物线型弯道等.要确定这些抛物线的形状,需要对地质、地形、气象、水力、材料等因素进行综合分析.二次函数的广泛应用
