2.7勾股定理的应用课件

课件23张PPT。八年级数学(苏科版) 2.7勾股定理的应用 （第二课时）
把勾股定理送到外星
球,与外星人进行数学交流 ！
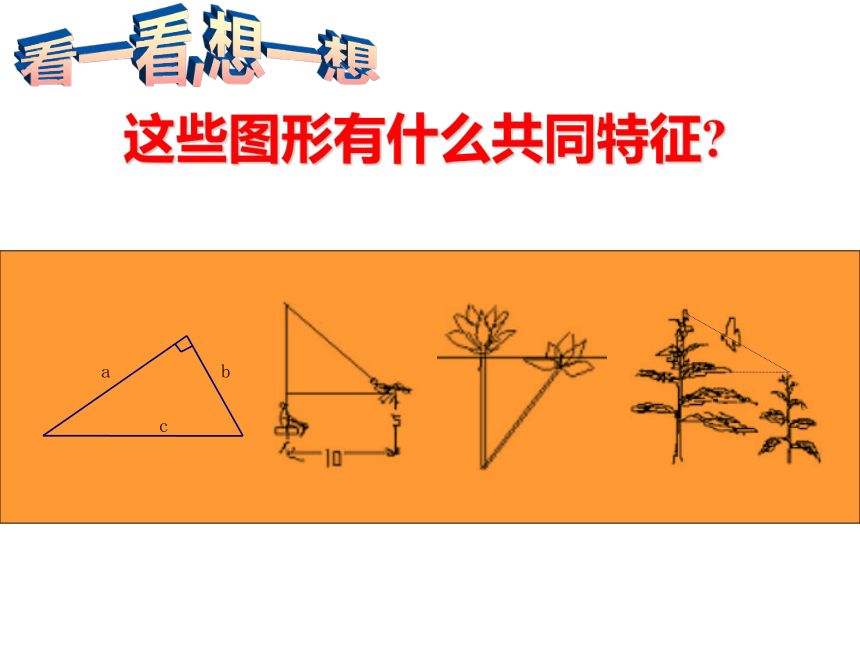
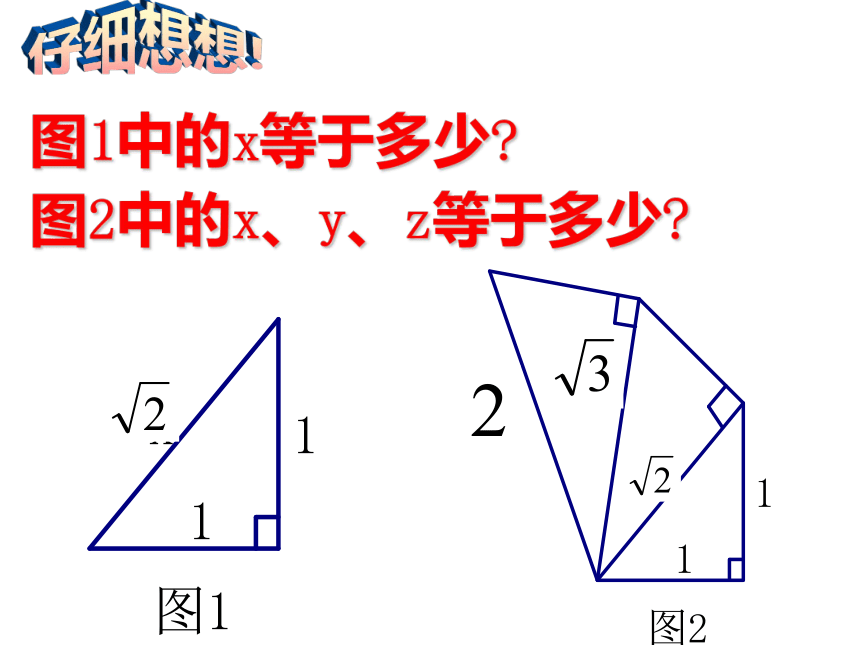
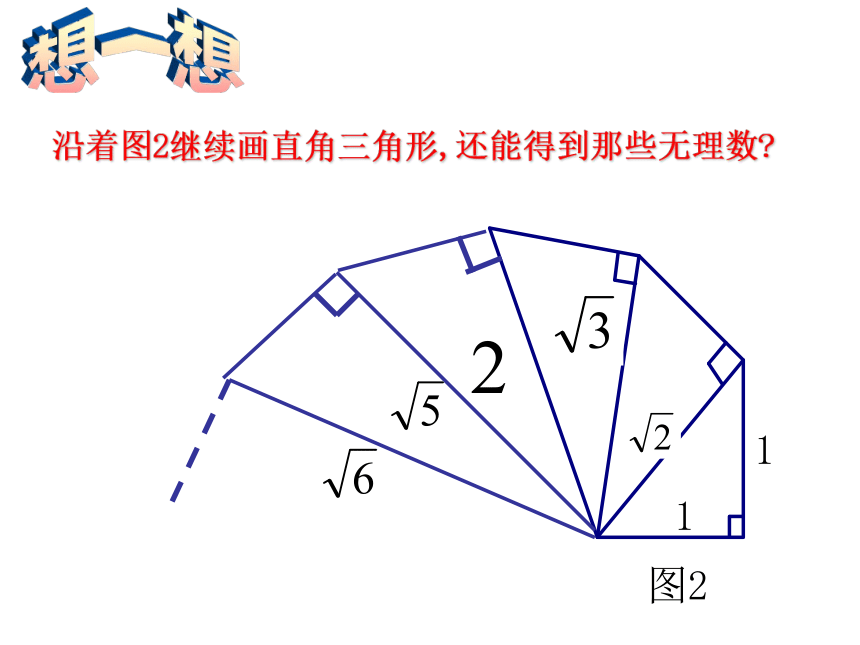
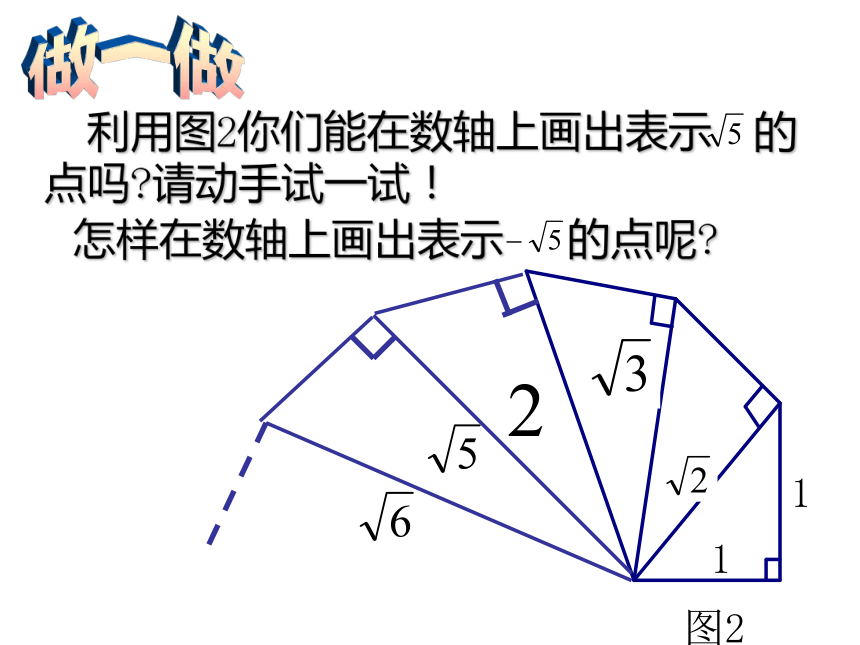
——华罗庚看一看,想一想这些图形有什么共同特征? 你是参加勾股定理应用交流的吗？是，请按“Yes”,不是请按“NO” 请完成下面几题，就取得交流资格! 图1中的x等于多少? 仔细想想!图2中的x、y、z等于多少? 想一想沿着图2继续画直角三角形,还能得到那些无理数? 做一做 利用图2你们能在数轴上画出表示 的点吗?请动手试一试！ 怎样在数轴上画出表示 的点呢? 拓展 在数轴上表示 ，
的点怎样画出?
图2中的图形的周长和面积分别是多少? 算一算周长是6 面积是 说一说 你们能说出 的实际意义吗？ 如图，求四边形ABCD的周长和面积。 拓展应用周长是68；
面积是246； 例1、如图，等边三角形ABC的边长是6，求△ABC的面积。 拓展应用 1、如图5，在△ABC中，AB=AC=17，BC=16，求△ABC的面积。 练一练2、如图6，在△ABC中，AD⊥BC，AB=15，AD=12，AC=13，求△ABC的周长和面积。 材料1：如图7，在△ABC中，AB=25，BC=7，AC=24，问△ABC是什么三角形？ 交流材料 材料2：如图8，在△ABC中，AB=26，BC=20，BC边上的中线AD=24，求AC. 交流材料交流材料材料3: 如图9，在△ABC中， AB=15，AD=12，BD=9,AC=13,求△ABC的周长和面积。 周长为42
面积为84 议一议 勾股定理与它的逆定理在应用上有什么区别？ 勾股定理主要应用于求线段的长度、图形的周长、面积；
勾股定理的逆定理用于判断三角形的形状。 试一试 如图，以△ABC的三边为直径向外作半圆，且S1+S3=S2，试判断△ABC的形状？ 应用 《引葭赴岸》
“今有池一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐，问水深，葭长各几何？”题意是：有一个边长为10尺的正方形池塘，一棵芦苇AB生长在它的中央，高出水面部分BC为一尺。如果把该芦苇沿与水池边垂直的方向拉向岸边，那么芦苇的顶部B恰好碰到岸边的B’.问水深和芦苇长各为多少？勾 股 定 理 的 应 用 勾 股 定 理 的 逆 定 理 的 应 用 小结1、数形结合思想2、转化思想
3、勾股定理与其逆定理在应用上的区别