青岛版(五四制)数学五年级下册 第四单元第2课《圆柱的表面积 课件(共22张PPT)
文档属性
| 名称 | 青岛版(五四制)数学五年级下册 第四单元第2课《圆柱的表面积 课件(共22张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 682.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-27 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
2.圆柱的表面积
第4单元冰淇淋盒有多大
学习目标
理解圆柱侧面积和圆柱表面积的含义,掌握圆柱侧面积和表面积的计算方法。
根据圆柱表面积和侧面积的关系,学会运用所学的知识解决简单的实际问题。
通过实践操作,理解圆柱侧面积和表面的含义的同时,培养理解能力和探索意识。
复习旧知
1、说一说圆柱各部分的名称及它的特征。
2、说一说圆锥各部分的名称及它的特征。
复习旧知
1、说说正方体的表面积是指什么?它的计算公式是什么?
正方体的表面积是指围成正方体6个面的面积总和。
情景导入
你能提出什么问题?
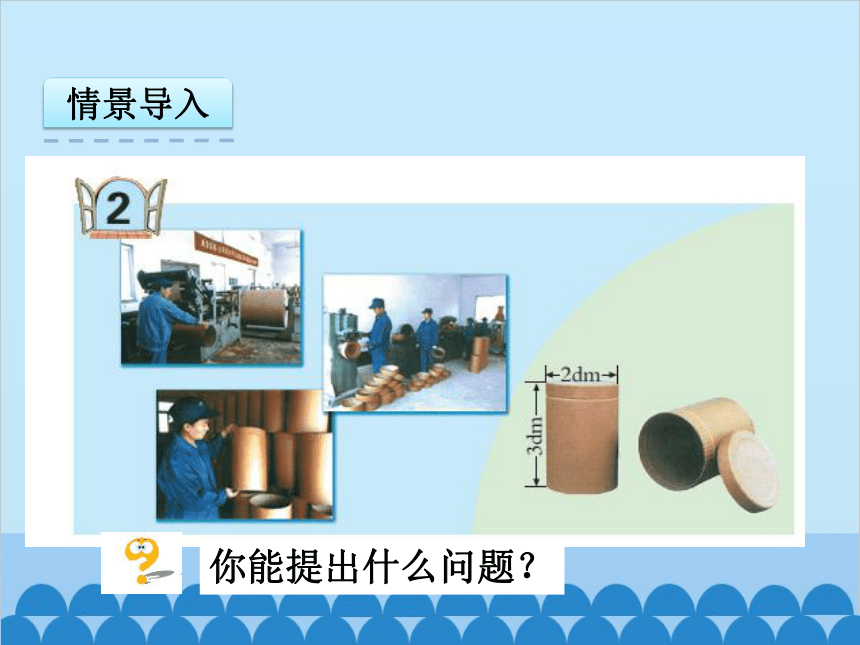
做这样一个纸筒,至少需要多少纸板?
做这样一个纸筒,至少需要多少纸板?
求需要多少纸板,就是求圆柱形纸筒的表面积。
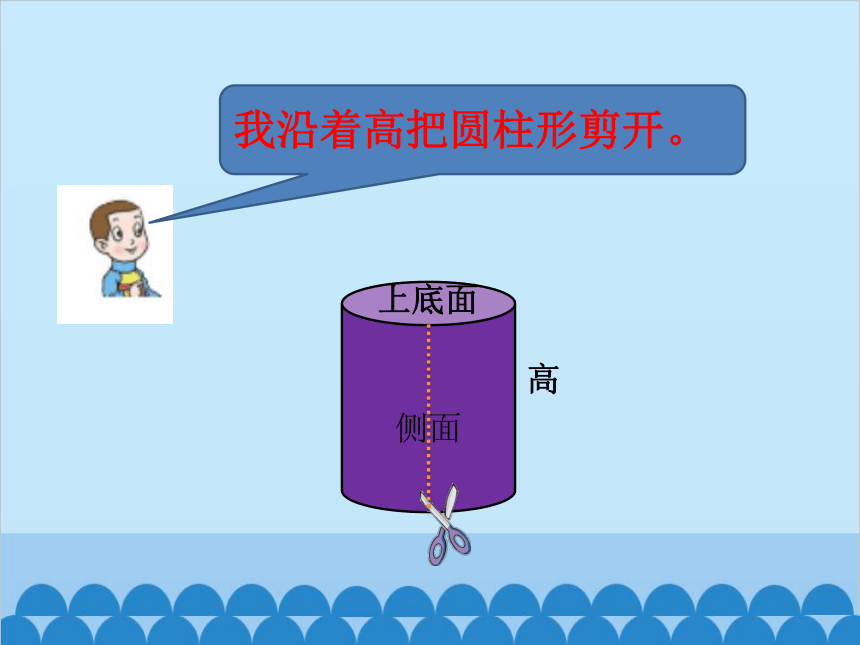
我沿着高把圆柱形剪开。
侧面
上底面
高
侧面
上底面
高
你发现了什么?
我发现圆柱的侧面积加上两个底面的面积就是圆柱的表面积。
S表= S侧+ 2S底
圆柱的表面积是什么?
圆柱的侧面展开后是一个长方形,长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高。
长方形的面积=长×宽
圆柱的侧面积=底面周长×高
S侧=ch
圆柱的侧面积=底面周长×高
用字母表示为:
圆柱的表面积公式为:
S表= S侧 + 2S底
我会求做圆柱形纸筒需要多少纸板了?
侧面积:
3.14×2×3=18.84(平方分米)
表面积:
18.84+3.14=21.96(平方分米)
答:做一个这样的纸筒,至少需要21.96平方分米。
典题精讲
右图是一个圆柱形铁皮油桶的表面展开图,做这个油桶至少需要铁皮多少平方分米?
12.56分米
5分米
思路点拨:
求油桶的表面积也就是求圆柱的表面积,题中告诉了底面周长,告诉了高,可以用“底面周长×高”求到侧面积,底面积可以先用“底面周长÷2π”得到半径,再用“半径的平方×π × 2”,求到底面积,最后与侧面积相加求到表面积。
典题精讲
右图是一个圆柱形铁皮油桶的表面展开图,做这个油桶至少需要铁皮多少平方分米?
12.56分米
5分米
解答过程:
3.14×(12.56 ÷ 3.14 ÷ 2) ×2+12.56 ×5
=3.14 ×4 ×2+62.8
=87.92(平方分米)
答:做这个油桶至少需要铁皮87.92平方分米。
一个圆柱的侧面沿高展开后是一个边长15.7厘米的正方形,这个圆柱的表面积是多少平方厘米?
解答:
侧面积:15.7 ×15.7=246.49(cm2)
半径:15.7 ÷2 ÷3.14=2.5(厘米)
答:这个圆柱的表面积是226.115cm2。
底面积:3.14 ×2.5 ×2.5=19.625(cm2)
表面积:246.49+19.625=226.115(cm2)
易错题型1
易错题型2
学校礼堂门前有5根圆柱形柱子,每根高3.2米,底面周长为1.25米。如果每平方米用油漆0.5千克,漆这5根柱子,需要油漆多少千克?
油漆漆在柱子的侧面,因此需要先求出一根柱子的侧面积,再算出一根柱子所用的油漆重量,再求出5根柱子需要油漆的重量。
3.2×1.25×0.5×5=10(千克)
答:需要油漆10千克。
学以致用
1、计算下面圆柱的表面积。(单位分米)
侧面积:
3.14×2×5×10=314(平方分米)
表面积:
314+157=471(平方分米)
学以致用
2.一根圆柱形木料,底面积是6平方分米,把它截成4段,表面积增加了多少平方分米?
想:表面积增加在切面的面积。截成4段,增加了6个切面。
6×6=36(平方分米)
答:表面积增加了36平方分米。
课堂小结
2.圆柱的表面积
第4单元冰淇淋盒有多大
学习目标
理解圆柱侧面积和圆柱表面积的含义,掌握圆柱侧面积和表面积的计算方法。
根据圆柱表面积和侧面积的关系,学会运用所学的知识解决简单的实际问题。
通过实践操作,理解圆柱侧面积和表面的含义的同时,培养理解能力和探索意识。
复习旧知
1、说一说圆柱各部分的名称及它的特征。
2、说一说圆锥各部分的名称及它的特征。
复习旧知
1、说说正方体的表面积是指什么?它的计算公式是什么?
正方体的表面积是指围成正方体6个面的面积总和。
情景导入
你能提出什么问题?
做这样一个纸筒,至少需要多少纸板?
做这样一个纸筒,至少需要多少纸板?
求需要多少纸板,就是求圆柱形纸筒的表面积。
我沿着高把圆柱形剪开。
侧面
上底面
高
侧面
上底面
高
你发现了什么?
我发现圆柱的侧面积加上两个底面的面积就是圆柱的表面积。
S表= S侧+ 2S底
圆柱的表面积是什么?
圆柱的侧面展开后是一个长方形,长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高。
长方形的面积=长×宽
圆柱的侧面积=底面周长×高
S侧=ch
圆柱的侧面积=底面周长×高
用字母表示为:
圆柱的表面积公式为:
S表= S侧 + 2S底
我会求做圆柱形纸筒需要多少纸板了?
侧面积:
3.14×2×3=18.84(平方分米)
表面积:
18.84+3.14=21.96(平方分米)
答:做一个这样的纸筒,至少需要21.96平方分米。
典题精讲
右图是一个圆柱形铁皮油桶的表面展开图,做这个油桶至少需要铁皮多少平方分米?
12.56分米
5分米
思路点拨:
求油桶的表面积也就是求圆柱的表面积,题中告诉了底面周长,告诉了高,可以用“底面周长×高”求到侧面积,底面积可以先用“底面周长÷2π”得到半径,再用“半径的平方×π × 2”,求到底面积,最后与侧面积相加求到表面积。
典题精讲
右图是一个圆柱形铁皮油桶的表面展开图,做这个油桶至少需要铁皮多少平方分米?
12.56分米
5分米
解答过程:
3.14×(12.56 ÷ 3.14 ÷ 2) ×2+12.56 ×5
=3.14 ×4 ×2+62.8
=87.92(平方分米)
答:做这个油桶至少需要铁皮87.92平方分米。
一个圆柱的侧面沿高展开后是一个边长15.7厘米的正方形,这个圆柱的表面积是多少平方厘米?
解答:
侧面积:15.7 ×15.7=246.49(cm2)
半径:15.7 ÷2 ÷3.14=2.5(厘米)
答:这个圆柱的表面积是226.115cm2。
底面积:3.14 ×2.5 ×2.5=19.625(cm2)
表面积:246.49+19.625=226.115(cm2)
易错题型1
易错题型2
学校礼堂门前有5根圆柱形柱子,每根高3.2米,底面周长为1.25米。如果每平方米用油漆0.5千克,漆这5根柱子,需要油漆多少千克?
油漆漆在柱子的侧面,因此需要先求出一根柱子的侧面积,再算出一根柱子所用的油漆重量,再求出5根柱子需要油漆的重量。
3.2×1.25×0.5×5=10(千克)
答:需要油漆10千克。
学以致用
1、计算下面圆柱的表面积。(单位分米)
侧面积:
3.14×2×5×10=314(平方分米)
表面积:
314+157=471(平方分米)
学以致用
2.一根圆柱形木料,底面积是6平方分米,把它截成4段,表面积增加了多少平方分米?
想:表面积增加在切面的面积。截成4段,增加了6个切面。
6×6=36(平方分米)
答:表面积增加了36平方分米。
课堂小结
