青岛版(五四制)数学五年级下册 2.1 图形与几何学案 (含答案)
文档属性
| 名称 | 青岛版(五四制)数学五年级下册 2.1 图形与几何学案 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 199.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-27 00:00:00 | ||
图片预览


文档简介
一、线段、射线、直线 1.线段、射线、直线的定义。 (1)线段:直线上两点和它们之间的部分叫作线段。 (2)射线:把线段向一个方向无限延长就形成了射线。 (3)直线:将线段向两个方向无限延长就可以得到一条直线。 2.线段、射线、直线的表示方法。 (1)线段的表示方法有两种:一是用两个端点来表示,二是用一个小写的英文字母来表示。 (2)射线的表示方法只有一种:用端点和射线上的另一个点来表示,端点要写在前面。 (3)直线的表示方法有两种:一是用直线上的两个点来表示,二是用一个小写的英文字母来表示。 3.直线性质:过两点有且只有一条直线。简称两点确定一条直线。 4.线段的比较。 (1)叠合比较法;(2)度量比较法。 5.线段性质:“两点之间,线段最短”。连接两点的线段的长度,叫作这两点间的距离。 6.线段的中点:如果线段上有一点,把线段分成相等的两条线段,这个点叫这条线段的中点。 若点C是线段AB的中点,则AC=BC=AB或AB=2AC=2BC。 二、平行与垂直 1.平行线的定义。 (1)在同一平面内的两条不相交的直线叫平行线。 (2)平行线用“∥”来表示。 2.画已知直线的平行线的方法:用直尺和三角板画平行线。 3.垂直的概念。 (1)如果两条直线相交成直角,那么这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫作垂足。 (2)两条线段互相垂直指它们所在的直线互相垂直。 (3)两条直线垂直用“⊥”来表示,如直线AB与直线CD垂直,记作:AB⊥BC。 4.垂直线段的概念。 (1)过一点A画直线a的垂线,垂足为B,则线段AB叫直线a的垂直线段。 (2)直线外一点A到直线a的垂直线段长度叫点A到直线a的距离。 三、角的认识 1.角的概念。 (1)角可以看成是由两条有共同端点的射线组成的图形。两条射线叫角的边,共同的端点叫角的顶点。 (2)角还可以看成是一条射线绕着它的端点旋转所成的图形。 2.角的表示方法。 角用“∠”符号表示。 (1)分别用两条边上的两个点和顶点来表示(顶点必须在中间)。 (2)在角的内部写上阿拉伯数字,然后用这个阿拉伯数字来表示角。 (3)在角的内部写上小写的希腊字母,然后用这个希腊字母来表示角。 (4)直接用一个大写英文字母来表示。 3.角的度量:会用量角器来度量角的大小。 4.锐角、直角、钝角、平角、周角的概念和大小。 (1)平角:角的两条边成一条直线时,这个角叫平角。 (2)周角:角的一边旋转一周,与另一边重合时,这个角叫周角。 (3)0°<锐角<90°,1直角=90°,90°<钝角<180°,1平角=180°,1周角=360°。 四、三角形 1.三角形的定义:由三条线段首尾顺次连接围成的图形叫三角形。 2.三角形各部分的名称:围成三角形的三条线段叫作三角形的边;每两条边的交点叫作三角形的顶点;每两条边所形成的角叫作三角形的内角。 一个三角形有三条边,三个顶点和三个内角。 从三角形的一个顶点向对边做一条垂线,顶点和垂足之间的线段叫作三角形的高。 一个三角形有三条高。 3.三角形的分类。 (1)按角分。 名称锐角三角形直角三角形钝角三角形图形特征三个角都是锐角有一个角是直角有一个角是钝角
(2)按边分。 名称不等边三角形等腰三角形图形特征三条边都不相等有两条边相等三条边都相等
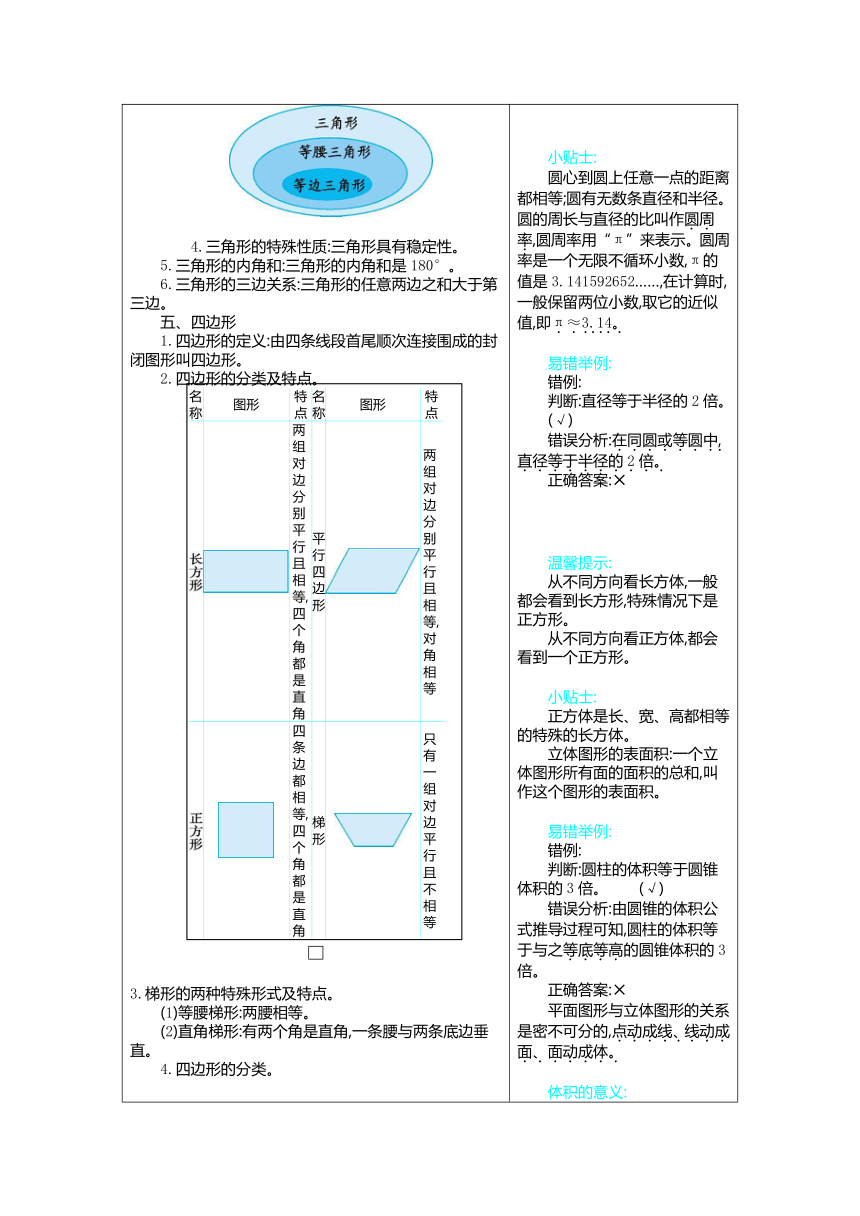
(3)等边三角形是特殊的等腰三角形,它们之间的关系如图所示。 4.三角形的特殊性质:三角形具有稳定性。 5.三角形的内角和:三角形的内角和是180°。 6.三角形的三边关系:三角形的任意两边之和大于第三边。 五、四边形 1.四边形的定义:由四条线段首尾顺次连接围成的封闭图形叫四边形。 2.四边形的分类及特点。 名称图形特点名称图形特点两组对边分别平行且相等,四个角都是直角平行四 边形两组对边分别平行且相等,对角相等四条边都相等,四个角都是直角梯形只有一组对边平行且不相等
3.梯形的两种特殊形式及特点。 (1)等腰梯形:两腰相等。 (2)直角梯形:有两个角是直角,一条腰与两条底边垂直。 4.四边形的分类。 六、圆 1.圆:圆是一种封闭的曲线图形。 (1)圆的各部分的名称 圆中心的一点叫作圆心,圆心一般用字母O表示;圆心到圆上任意一点的线段叫作半径,半径用字母r表示;通过圆心并且两端都在圆上的线段叫作直径,直径用字母d表示。 (2)特征。 ①在同圆或等圆中,d=2r或r=。 ②圆是轴对称图形,圆的直径所在的直线都是它的对称轴,圆有无数条对称轴。 2.圆环(如右图)。 七、立体图形的认识 1.常见的立体图形有长方体、正方体、圆柱、圆锥、球。 2.长方体和正方体的特征。 (1)长方体的特征。 ①长方体有6个面,12条棱,8个顶点。 ②6个面一般都是长方形,特殊情况下可能有两个相对的面是正方形,相对的面的面积完全相等。 ③棱长 相对的棱的长度相等,长方体的棱长总和=4×(长+宽+高) (2)正方体的特征。 ①正方体有6个面,12条棱,8个顶点。 ②6个面 都是完全相同的正方形,6个面的面积都相等。 ③棱长 12条棱的长度都相等,正方体的棱长总和=12×棱长 (3)长、宽、高的意义。 相交于同一顶点的三条棱的长度分别叫作长方体的长、宽、高。 3.圆柱和圆锥的特征。 名称图形特征从不同方向看到 的图形圆柱1.圆柱有3个面,上、下两个底面是大小相等的圆,侧面是曲面 2.圆柱两个底面之间的距离叫作圆柱的高,圆柱有无数条高 3.圆柱的侧面沿高展开后是长方形或者正方形 4.以长方形或正方形的一边为轴旋转一周形成圆柱1.从上面或下面看,会看到一个圆 2.从侧面看会看到一个长方形或者正方形圆锥1.圆锥有2个面,它的底面是圆,侧面是曲面 2.圆锥的顶点到底面圆心的距离叫作圆锥的高,圆锥只有一条高 3.以三角形的一条直角边为轴旋转一周形成圆锥1.从上面看,会看到一个点 2.从下面看会看到一个圆 3.从侧面看会看到一个三角形
八、平面图形和立体图形的有关知识 名称特征计算公式长方形对边相等,四个角都是直角C=2(a+b) S=ab正方形四条边都相等,四个角都是直角C=4a S=a2梯形上底和下底互相平行,有四个角S=(a+b)h÷2平行四边形对边平行且相等,有四个角且对 角相等S=ah圆所有的半径都相等,直径都相等C=πd S=πr2长方体6个面,8个顶点,12条棱,对面相等S表=2(ab+ah+bh) V=abh正方体6个面,8个顶点,12条棱,6个面都相等S表=6a2 V=a3圆柱有3个面,上、下两个底面是大小相等的圆,侧面是曲面S侧=Ch V=Sh圆锥有2个面,一个底面是圆,一个侧面是曲面V=Sh
九、平面图形面积公式的推导 十、立体图形体积公式的推导 温馨提示: 线段有两个端点,线段可以量出长度。 射线有一个端点,射线无法量出长度。 直线没有端点,直线无法量出长度。 易错举例: 错例: 判断:直线比射线长。( ) 错误分析:直线没有端点,无法量出长度;射线有一个端点,也无法量出长度。因此两者不能比较,故本题说法错误。 正确答案: 温馨提示: 强调要在同一平面内,若不在同一平面内的两条直线,既不平行,又不相交,叫异面直线。 小贴士: 线段、射线的平行关系根据它所在的直线来确定,若它们所在的直线不相交,就平行;若所在的直线相交,就不平行。 特别提示: 角的大小与两边的长短无关,与两边叉开的大小有关。 易错举例: 错例: 判断:角的两边越长,角的度数越大。 (√) 正确答案: 温馨提示: 任意三角形都有三条高,锐角三角形的三条高都在三角形内部;钝角三角形有一条高在三角形内部,另外两条高在三角形的外部;直角三角形的一条高在三角形内部,另外两条高是三角形的两条边。 易错举例: 错例: 判断:三角形可以分为锐角三角形、直角三角形和等腰三角形。 (√) 错误分析:三角形的分类有两种,一是按角分,一是按边分,分类的标准不能混淆。 正确答案: 小贴士: 长方形是轴对称图形,它有2条对称轴;正方形是轴对称图形,它有4条对称轴;等腰梯形是轴对称图形,它有1条对称轴。 平行四边形不是轴对称图形。 温馨提示: 正方形是特殊的长方形;正方形和长方形都是特殊的平行四边形;等腰梯形和直角梯形都是特殊的梯形。 小贴士: 圆心到圆上任意一点的距离都相等;圆有无数条直径和半径。圆的周长与直径的比叫作圆周率,圆周率用“π”来表示。圆周率是一个无限不循环小数,π的值是3.141592652……,在计算时,一般保留两位小数,取它的近似值,即π≈3.14。 易错举例: 错例: 判断:直径等于半径的2倍。 (√) 错误分析:在同圆或等圆中,直径等于半径的2倍。 正确答案: 温馨提示: 从不同方向看长方体,一般都会看到长方形,特殊情况下是正方形。 从不同方向看正方体,都会看到一个正方形。 小贴士: 正方体是长、宽、高都相等的特殊的长方体。 立体图形的表面积:一个立体图形所有面的面积的总和,叫作这个图形的表面积。 易错举例: 错例: 判断:圆柱的体积等于圆锥体积的3倍。 (√) 错误分析:由圆锥的体积公式推导过程可知,圆柱的体积等于与之等底等高的圆锥体积的3倍。 正确答案: 平面图形与立体图形的关系是密不可分的,点动成线、线动成面、面动成体。 体积的意义: 物体所占空间的大小叫作物体的体积。 计量物体的体积要用体积单位。常见的体积单位有立方厘米、立方分米、立方米。 温馨提示: 一个容器所能容纳的物体的体积,叫作这个容器的容积。 计量液体的体积常用容积单位。常用的容积单位有升和毫升。升用字母“L”表示,毫升用字母“mL”表示。 小贴士: 长方体、正方体、圆柱的体积都可以用“底面积×高”来计算。 如果一个图形沿着一条直线对折,折痕两旁的图形能够完全重合,这个图形叫作轴对称图形,折痕所在的直线叫作对称轴。
(2)按边分。 名称不等边三角形等腰三角形图形特征三条边都不相等有两条边相等三条边都相等
(3)等边三角形是特殊的等腰三角形,它们之间的关系如图所示。 4.三角形的特殊性质:三角形具有稳定性。 5.三角形的内角和:三角形的内角和是180°。 6.三角形的三边关系:三角形的任意两边之和大于第三边。 五、四边形 1.四边形的定义:由四条线段首尾顺次连接围成的封闭图形叫四边形。 2.四边形的分类及特点。 名称图形特点名称图形特点两组对边分别平行且相等,四个角都是直角平行四 边形两组对边分别平行且相等,对角相等四条边都相等,四个角都是直角梯形只有一组对边平行且不相等
3.梯形的两种特殊形式及特点。 (1)等腰梯形:两腰相等。 (2)直角梯形:有两个角是直角,一条腰与两条底边垂直。 4.四边形的分类。 六、圆 1.圆:圆是一种封闭的曲线图形。 (1)圆的各部分的名称 圆中心的一点叫作圆心,圆心一般用字母O表示;圆心到圆上任意一点的线段叫作半径,半径用字母r表示;通过圆心并且两端都在圆上的线段叫作直径,直径用字母d表示。 (2)特征。 ①在同圆或等圆中,d=2r或r=。 ②圆是轴对称图形,圆的直径所在的直线都是它的对称轴,圆有无数条对称轴。 2.圆环(如右图)。 七、立体图形的认识 1.常见的立体图形有长方体、正方体、圆柱、圆锥、球。 2.长方体和正方体的特征。 (1)长方体的特征。 ①长方体有6个面,12条棱,8个顶点。 ②6个面一般都是长方形,特殊情况下可能有两个相对的面是正方形,相对的面的面积完全相等。 ③棱长 相对的棱的长度相等,长方体的棱长总和=4×(长+宽+高) (2)正方体的特征。 ①正方体有6个面,12条棱,8个顶点。 ②6个面 都是完全相同的正方形,6个面的面积都相等。 ③棱长 12条棱的长度都相等,正方体的棱长总和=12×棱长 (3)长、宽、高的意义。 相交于同一顶点的三条棱的长度分别叫作长方体的长、宽、高。 3.圆柱和圆锥的特征。 名称图形特征从不同方向看到 的图形圆柱1.圆柱有3个面,上、下两个底面是大小相等的圆,侧面是曲面 2.圆柱两个底面之间的距离叫作圆柱的高,圆柱有无数条高 3.圆柱的侧面沿高展开后是长方形或者正方形 4.以长方形或正方形的一边为轴旋转一周形成圆柱1.从上面或下面看,会看到一个圆 2.从侧面看会看到一个长方形或者正方形圆锥1.圆锥有2个面,它的底面是圆,侧面是曲面 2.圆锥的顶点到底面圆心的距离叫作圆锥的高,圆锥只有一条高 3.以三角形的一条直角边为轴旋转一周形成圆锥1.从上面看,会看到一个点 2.从下面看会看到一个圆 3.从侧面看会看到一个三角形
八、平面图形和立体图形的有关知识 名称特征计算公式长方形对边相等,四个角都是直角C=2(a+b) S=ab正方形四条边都相等,四个角都是直角C=4a S=a2梯形上底和下底互相平行,有四个角S=(a+b)h÷2平行四边形对边平行且相等,有四个角且对 角相等S=ah圆所有的半径都相等,直径都相等C=πd S=πr2长方体6个面,8个顶点,12条棱,对面相等S表=2(ab+ah+bh) V=abh正方体6个面,8个顶点,12条棱,6个面都相等S表=6a2 V=a3圆柱有3个面,上、下两个底面是大小相等的圆,侧面是曲面S侧=Ch V=Sh圆锥有2个面,一个底面是圆,一个侧面是曲面V=Sh
九、平面图形面积公式的推导 十、立体图形体积公式的推导 温馨提示: 线段有两个端点,线段可以量出长度。 射线有一个端点,射线无法量出长度。 直线没有端点,直线无法量出长度。 易错举例: 错例: 判断:直线比射线长。( ) 错误分析:直线没有端点,无法量出长度;射线有一个端点,也无法量出长度。因此两者不能比较,故本题说法错误。 正确答案: 温馨提示: 强调要在同一平面内,若不在同一平面内的两条直线,既不平行,又不相交,叫异面直线。 小贴士: 线段、射线的平行关系根据它所在的直线来确定,若它们所在的直线不相交,就平行;若所在的直线相交,就不平行。 特别提示: 角的大小与两边的长短无关,与两边叉开的大小有关。 易错举例: 错例: 判断:角的两边越长,角的度数越大。 (√) 正确答案: 温馨提示: 任意三角形都有三条高,锐角三角形的三条高都在三角形内部;钝角三角形有一条高在三角形内部,另外两条高在三角形的外部;直角三角形的一条高在三角形内部,另外两条高是三角形的两条边。 易错举例: 错例: 判断:三角形可以分为锐角三角形、直角三角形和等腰三角形。 (√) 错误分析:三角形的分类有两种,一是按角分,一是按边分,分类的标准不能混淆。 正确答案: 小贴士: 长方形是轴对称图形,它有2条对称轴;正方形是轴对称图形,它有4条对称轴;等腰梯形是轴对称图形,它有1条对称轴。 平行四边形不是轴对称图形。 温馨提示: 正方形是特殊的长方形;正方形和长方形都是特殊的平行四边形;等腰梯形和直角梯形都是特殊的梯形。 小贴士: 圆心到圆上任意一点的距离都相等;圆有无数条直径和半径。圆的周长与直径的比叫作圆周率,圆周率用“π”来表示。圆周率是一个无限不循环小数,π的值是3.141592652……,在计算时,一般保留两位小数,取它的近似值,即π≈3.14。 易错举例: 错例: 判断:直径等于半径的2倍。 (√) 错误分析:在同圆或等圆中,直径等于半径的2倍。 正确答案: 温馨提示: 从不同方向看长方体,一般都会看到长方形,特殊情况下是正方形。 从不同方向看正方体,都会看到一个正方形。 小贴士: 正方体是长、宽、高都相等的特殊的长方体。 立体图形的表面积:一个立体图形所有面的面积的总和,叫作这个图形的表面积。 易错举例: 错例: 判断:圆柱的体积等于圆锥体积的3倍。 (√) 错误分析:由圆锥的体积公式推导过程可知,圆柱的体积等于与之等底等高的圆锥体积的3倍。 正确答案: 平面图形与立体图形的关系是密不可分的,点动成线、线动成面、面动成体。 体积的意义: 物体所占空间的大小叫作物体的体积。 计量物体的体积要用体积单位。常见的体积单位有立方厘米、立方分米、立方米。 温馨提示: 一个容器所能容纳的物体的体积,叫作这个容器的容积。 计量液体的体积常用容积单位。常用的容积单位有升和毫升。升用字母“L”表示,毫升用字母“mL”表示。 小贴士: 长方体、正方体、圆柱的体积都可以用“底面积×高”来计算。 如果一个图形沿着一条直线对折,折痕两旁的图形能够完全重合,这个图形叫作轴对称图形,折痕所在的直线叫作对称轴。
