青岛版(五四制)数学五年级下册 《图形的认识与测量》 课件(共40张PPT)
文档属性
| 名称 | 青岛版(五四制)数学五年级下册 《图形的认识与测量》 课件(共40张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-27 12:47:18 | ||
图片预览





文档简介
(共40张PPT)
6.图形的认识与测量
第8单元回顾整理
学习目标
加深对长方形、正方形、平行四边形、梯形、三角形圆、长方体、正方体、圆柱、圆锥等平面图形、立体图形基本特征的认识,进一步理解这些图形之间的关系,完善认知结构。
进一步体会平面图形与现实生活的密切联系,积累学习有关平面图形知识的经验和方法,发展简单的推理能力,增强空间观念。
进一步感受空间与图形领域学习内容的趣味性和挑战性,产生继续探索学习的积极心态,增强学好数学的信心。
复习旧知
小学阶段我们学过哪些平面图形和立体图形?
长方形、正方形、三角形、平行四边、梯形、圆
长方体、正方体、圆柱、圆锥
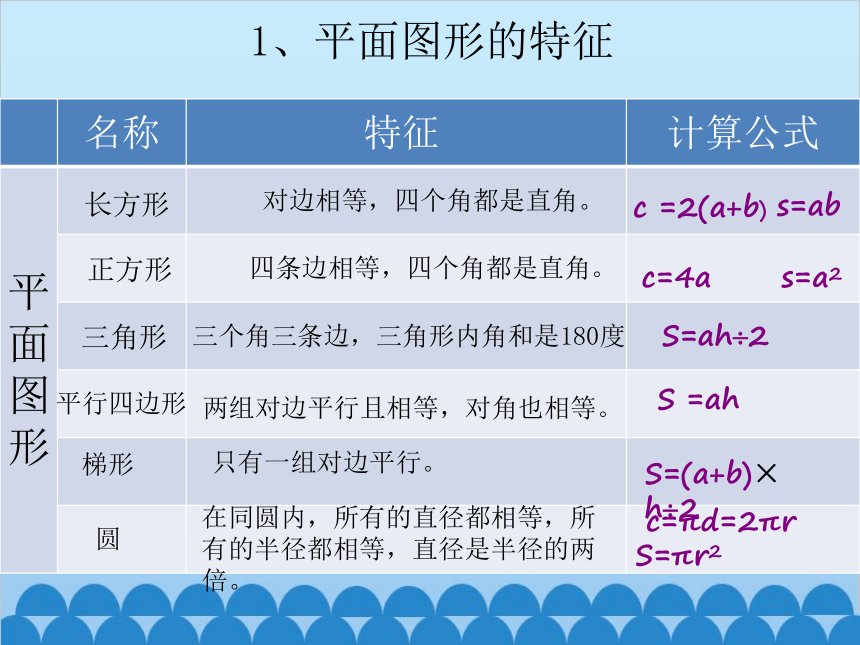
1、平面图形的特征
名称 特征 计算公式
平面图形
对边相等,四个角都是直角。
s=ab
c =2(a+b)
长方形
正方形
四条边相等,四个角都是直角。
s=a2
c=4a
三角形
三个角三条边,三角形内角和是180度
S=ah 2
平行四边形
两组对边平行且相等,对角也相等。
S =ah
梯形
只有一组对边平行。
S=(a+b)× h 2
圆
在同圆内,所有的直径都相等,所有的半径都相等,直径是半径的两倍。
c=πd=2πr
S=πr2
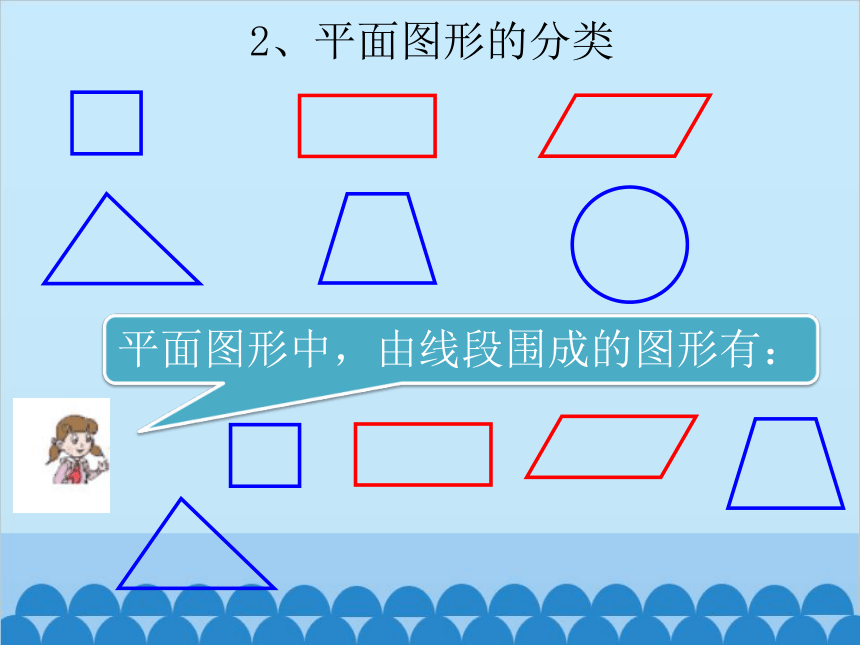
2、平面图形的分类
平面图形中,由线段围成的图形有:
3、长方体、正方体的特征
名称 特征 计算公式
立体图形
长方体
8个顶点,12条棱,相对的棱长相等。6个面,相对的面完全相同,特殊情况两个相对面为正方形。
s=2(ab+ah+bh)
v=abh或v=sh
正方体
8个顶点, 12条棱相等。6个面都是完全一样的正方形。
v=a3
s=a2
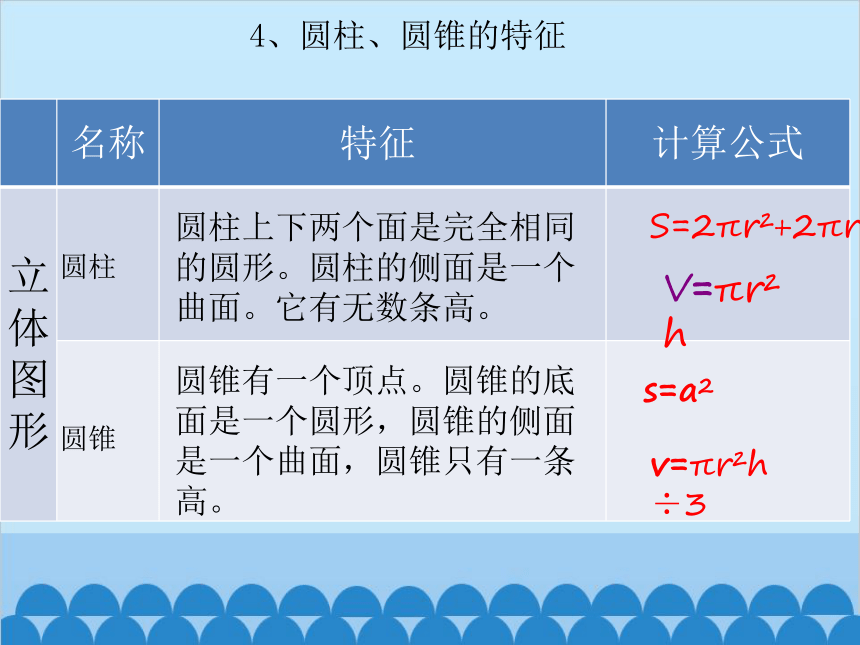
4、圆柱、圆锥的特征
名称 特征 计算公式
立体图形
圆柱
圆柱上下两个面是完全相同的圆形。圆柱的侧面是一个曲面。它有无数条高。
S=2πr +2πrh
V=πr h
圆锥
圆锥有一个顶点。圆锥的底面是一个圆形,圆锥的侧面是一个曲面,圆锥只有一条高。
v=πr h ÷3
s=a2
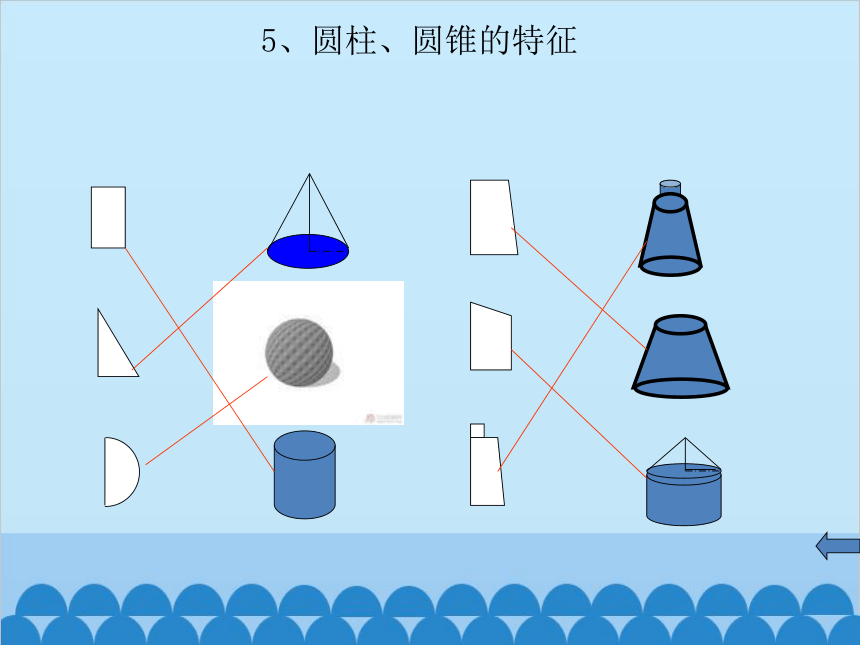
5、圆柱、圆锥的特征
我们学过的平面图形的面积计算公式是怎样推导出来的?它们之间有怎样的联系?
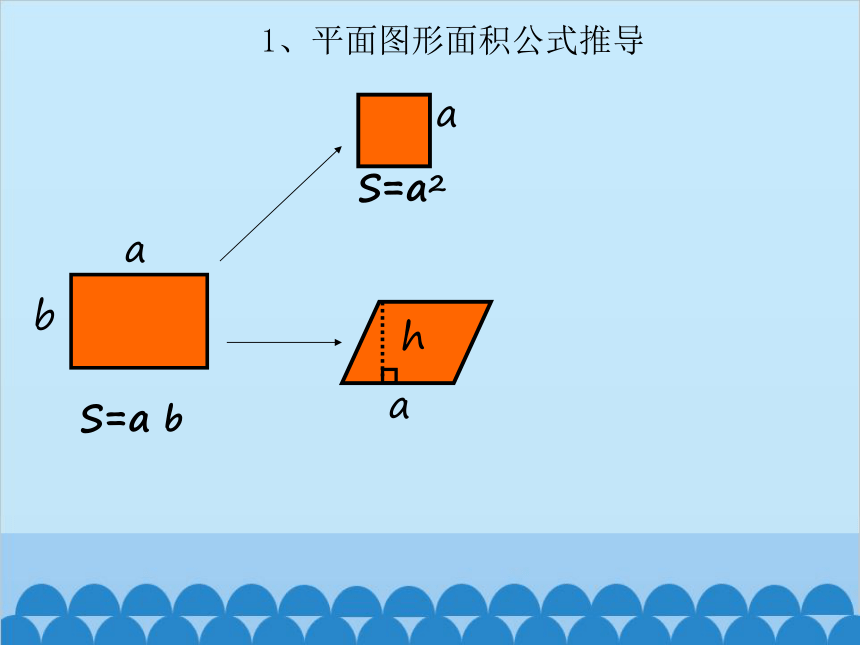
1、平面图形面积公式推导
a
b
S=a b
a
S=a2
a
h
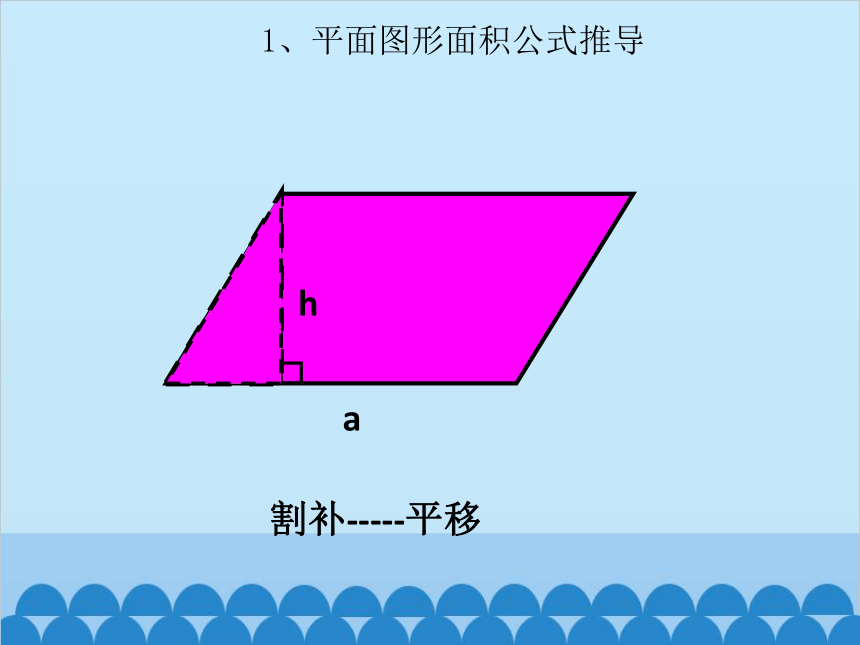
1、平面图形面积公式推导
h
a
割补-----平移
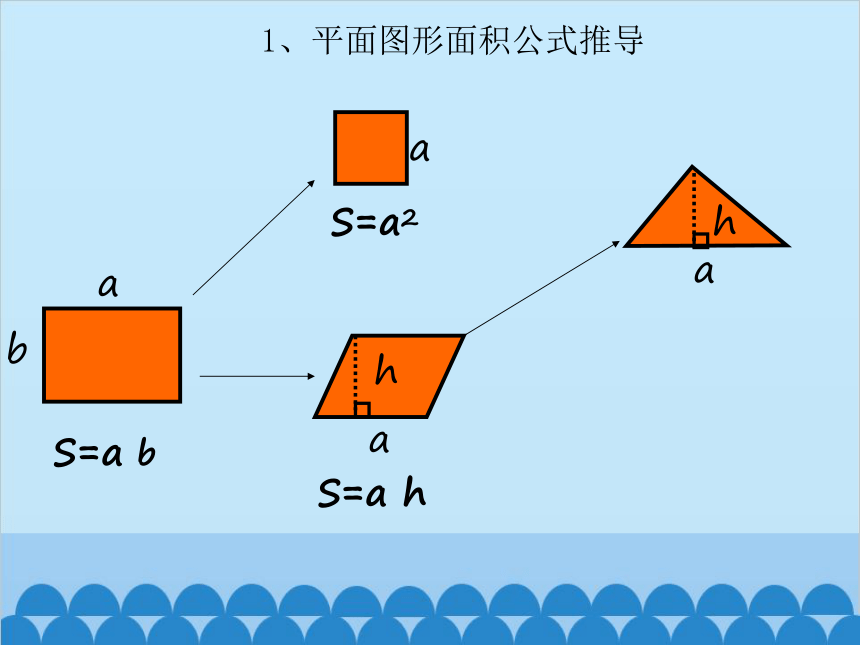
1、平面图形面积公式推导
a
b
S=a b
a
S=a2
a
h
S=a h
a
h
1、平面图形面积公式推导
a
h
旋转 ----- 平移 ----- 拼
1、平面图形面积公式推导
a
b
S=a b
a
S=a2
a
h
S=a h
a
h
S=a h÷2
a
b
h
1、平面图形面积公式推导
h
a
b
旋转----- 平移 ----- 拼
1、平面图形面积公式推导
a
b
S=a b
a
S=a2
a
h
S=a h
a
h
S=a h÷2
a
b
h
r
S=(a+b)h÷2
1、平面图形面积公式推导
r
πr
切拼
a
b
S=a b
a
S=a2
a
h
S=a h
a
h
S=a h÷2
a
b
h
r
S=(a+b)h÷2
S= π r
1、平面图形面积公式推导
2、立体图形体积公式推导
我们学过的立体图形的体积计算公式是怎样推导出来的?它们之间有怎样的联系?
ɑ
ɑ
b
h
h
r
S
h
V= ɑbh
V= ɑ
3
V= π r h
2
V= Sh
2、立体图形体积公式推导
ɑ
ɑ
b
h
h
r
S
h
V= ɑbh
V= ɑ
3
V= π r h
2
V= Sh
2、立体图形体积公式推导
ɑ
ɑ
b
h
h
r
S
h
V= ɑbh
V= ɑ
3
V= π r h
2
V= Sh
2、立体图形体积公式推导
ɑ
ɑ
b
h
h
r
S
h
V= ɑbh
V= ɑ
3
V= π r h
2
V= Sh
2、立体图形体积公式推导
ɑ
ɑ
b
h
h
r
S
h
V= ɑbh
V= ɑ
3
V= π r h
2
V= Sh
V=Sh
2、立体图形体积公式推导
选择下面的材料制作一个水桶,有几个方案?
底面可以是什么形状?侧面是什么形?
典题精讲
解题思路:
求小路的面积实际上就是求环形的面积,已知花坛的直径是16米,可以求出小圆的半径是16÷2=8(米),而外边大圆的半径是2+8=10(米),再根据求环形面积的公式就可以求出这条小路的面积是多少平方米。
在一个直径是16米的圆形花坛周围,修一条宽2米的小路,这条小路的面积是多少平方米
典题精讲
解答:
易错题型
易错分析:
错在将半圆的周长理解成周长的一半了,实际上半圆的周长是圆的周长的一半加上一条直径的长度。
易错题型
典题精讲
解题思路:
这道题是对观察物体这一知识点的运用,这是一个由6个小正方体组成的立体图形,从上面看分为前,后两排,每排各两个小正方形,从正面看分为上、下两层,上面一层有一个小正方形,下面一层有两个小正方形。
画出下面图形从上面、正面看到的立体图形的形状。
典题精讲
解答:
画出下面图形从上面、正面看到的立体图形的形状。
正面
上面
易错题型
如图,把一个棱长为3的正方体的每个面等分成9个小正方形,然后沿每个面正中心的一个正方形向里挖空(相当于挖去7个小正方体),所得到的几何体的表面积是(A)
A、78 B、72 C、54 D、48
易错分析:
如图所示,棱长为3的正方体的每个面等分成9个小正方形,那么每个小正方形的边长是1,所以每个小正方面的面积是1;正方体的一个面有9个小正方形,挖空后,这个面的表面积增加了4个小正方形,即:每个面有12个小正方形,6个面就是6×12=72个,那么几何体的表面积为72×1=72。
易错题型
如图,把一个棱长为3的正方体的每个面等分成9个小正方形,然后沿每个面正中心的一个正方形向里挖空(相当于挖去7个小正方体),所得到的几何体的表面积是(A)
A、78 B、72 C、54 D、48
正确解答:
解:如图所示,周边的六个挖空的正方体每个面增加4个正方形,则每个面的正方形个数为12个,则表面积为12×6×1=72。 故选B。
学以致用
1.A、B两镇位于河岸同侧,它们到
河岸的距离分别为AC、BD,现要在岸
边CD上建一水塔给两镇送水,问水塔
建在何处使水管最省?
A
B
C
D
A1
B1
F
G
E
E
学以致用
2.下面第一排中的平面图形,绕红线旋转一周能形成第二排的哪个立体图形?(连线)
学以致用
3.下面这个容器一共能装多少毫升水 (容器壁的厚度忽略不计)
学以致用
4.一条水渠长800米,横截面如下图。
(1)水渠的横截面积是多少平方米?
4×2.5=10(平方米)
答:水渠的横截面积是10平方米。
学以致用
4.一条水渠长800米,横截面如下图。
(2)水渠水深2米,水在水渠中每分流动20米,该水渠每时的水流量是多少立方米?
4×2.5×20×60=12000(立方米)
答:该水渠每时的水流量是12000立方米。
学以致用
5.学校修建花园需要40吨沙,这堆沙够用吗?(每立方米沙重1.8吨。)
底面周长12.56米。
高1.2米。
这节课,我们复面图形和立体图形的特征和相关的知识,你掌握了吗?
课堂小结
6.图形的认识与测量
第8单元回顾整理
学习目标
加深对长方形、正方形、平行四边形、梯形、三角形圆、长方体、正方体、圆柱、圆锥等平面图形、立体图形基本特征的认识,进一步理解这些图形之间的关系,完善认知结构。
进一步体会平面图形与现实生活的密切联系,积累学习有关平面图形知识的经验和方法,发展简单的推理能力,增强空间观念。
进一步感受空间与图形领域学习内容的趣味性和挑战性,产生继续探索学习的积极心态,增强学好数学的信心。
复习旧知
小学阶段我们学过哪些平面图形和立体图形?
长方形、正方形、三角形、平行四边、梯形、圆
长方体、正方体、圆柱、圆锥
1、平面图形的特征
名称 特征 计算公式
平面图形
对边相等,四个角都是直角。
s=ab
c =2(a+b)
长方形
正方形
四条边相等,四个角都是直角。
s=a2
c=4a
三角形
三个角三条边,三角形内角和是180度
S=ah 2
平行四边形
两组对边平行且相等,对角也相等。
S =ah
梯形
只有一组对边平行。
S=(a+b)× h 2
圆
在同圆内,所有的直径都相等,所有的半径都相等,直径是半径的两倍。
c=πd=2πr
S=πr2
2、平面图形的分类
平面图形中,由线段围成的图形有:
3、长方体、正方体的特征
名称 特征 计算公式
立体图形
长方体
8个顶点,12条棱,相对的棱长相等。6个面,相对的面完全相同,特殊情况两个相对面为正方形。
s=2(ab+ah+bh)
v=abh或v=sh
正方体
8个顶点, 12条棱相等。6个面都是完全一样的正方形。
v=a3
s=a2
4、圆柱、圆锥的特征
名称 特征 计算公式
立体图形
圆柱
圆柱上下两个面是完全相同的圆形。圆柱的侧面是一个曲面。它有无数条高。
S=2πr +2πrh
V=πr h
圆锥
圆锥有一个顶点。圆锥的底面是一个圆形,圆锥的侧面是一个曲面,圆锥只有一条高。
v=πr h ÷3
s=a2
5、圆柱、圆锥的特征
我们学过的平面图形的面积计算公式是怎样推导出来的?它们之间有怎样的联系?
1、平面图形面积公式推导
a
b
S=a b
a
S=a2
a
h
1、平面图形面积公式推导
h
a
割补-----平移
1、平面图形面积公式推导
a
b
S=a b
a
S=a2
a
h
S=a h
a
h
1、平面图形面积公式推导
a
h
旋转 ----- 平移 ----- 拼
1、平面图形面积公式推导
a
b
S=a b
a
S=a2
a
h
S=a h
a
h
S=a h÷2
a
b
h
1、平面图形面积公式推导
h
a
b
旋转----- 平移 ----- 拼
1、平面图形面积公式推导
a
b
S=a b
a
S=a2
a
h
S=a h
a
h
S=a h÷2
a
b
h
r
S=(a+b)h÷2
1、平面图形面积公式推导
r
πr
切拼
a
b
S=a b
a
S=a2
a
h
S=a h
a
h
S=a h÷2
a
b
h
r
S=(a+b)h÷2
S= π r
1、平面图形面积公式推导
2、立体图形体积公式推导
我们学过的立体图形的体积计算公式是怎样推导出来的?它们之间有怎样的联系?
ɑ
ɑ
b
h
h
r
S
h
V= ɑbh
V= ɑ
3
V= π r h
2
V= Sh
2、立体图形体积公式推导
ɑ
ɑ
b
h
h
r
S
h
V= ɑbh
V= ɑ
3
V= π r h
2
V= Sh
2、立体图形体积公式推导
ɑ
ɑ
b
h
h
r
S
h
V= ɑbh
V= ɑ
3
V= π r h
2
V= Sh
2、立体图形体积公式推导
ɑ
ɑ
b
h
h
r
S
h
V= ɑbh
V= ɑ
3
V= π r h
2
V= Sh
2、立体图形体积公式推导
ɑ
ɑ
b
h
h
r
S
h
V= ɑbh
V= ɑ
3
V= π r h
2
V= Sh
V=Sh
2、立体图形体积公式推导
选择下面的材料制作一个水桶,有几个方案?
底面可以是什么形状?侧面是什么形?
典题精讲
解题思路:
求小路的面积实际上就是求环形的面积,已知花坛的直径是16米,可以求出小圆的半径是16÷2=8(米),而外边大圆的半径是2+8=10(米),再根据求环形面积的公式就可以求出这条小路的面积是多少平方米。
在一个直径是16米的圆形花坛周围,修一条宽2米的小路,这条小路的面积是多少平方米
典题精讲
解答:
易错题型
易错分析:
错在将半圆的周长理解成周长的一半了,实际上半圆的周长是圆的周长的一半加上一条直径的长度。
易错题型
典题精讲
解题思路:
这道题是对观察物体这一知识点的运用,这是一个由6个小正方体组成的立体图形,从上面看分为前,后两排,每排各两个小正方形,从正面看分为上、下两层,上面一层有一个小正方形,下面一层有两个小正方形。
画出下面图形从上面、正面看到的立体图形的形状。
典题精讲
解答:
画出下面图形从上面、正面看到的立体图形的形状。
正面
上面
易错题型
如图,把一个棱长为3的正方体的每个面等分成9个小正方形,然后沿每个面正中心的一个正方形向里挖空(相当于挖去7个小正方体),所得到的几何体的表面积是(A)
A、78 B、72 C、54 D、48
易错分析:
如图所示,棱长为3的正方体的每个面等分成9个小正方形,那么每个小正方形的边长是1,所以每个小正方面的面积是1;正方体的一个面有9个小正方形,挖空后,这个面的表面积增加了4个小正方形,即:每个面有12个小正方形,6个面就是6×12=72个,那么几何体的表面积为72×1=72。
易错题型
如图,把一个棱长为3的正方体的每个面等分成9个小正方形,然后沿每个面正中心的一个正方形向里挖空(相当于挖去7个小正方体),所得到的几何体的表面积是(A)
A、78 B、72 C、54 D、48
正确解答:
解:如图所示,周边的六个挖空的正方体每个面增加4个正方形,则每个面的正方形个数为12个,则表面积为12×6×1=72。 故选B。
学以致用
1.A、B两镇位于河岸同侧,它们到
河岸的距离分别为AC、BD,现要在岸
边CD上建一水塔给两镇送水,问水塔
建在何处使水管最省?
A
B
C
D
A1
B1
F
G
E
E
学以致用
2.下面第一排中的平面图形,绕红线旋转一周能形成第二排的哪个立体图形?(连线)
学以致用
3.下面这个容器一共能装多少毫升水 (容器壁的厚度忽略不计)
学以致用
4.一条水渠长800米,横截面如下图。
(1)水渠的横截面积是多少平方米?
4×2.5=10(平方米)
答:水渠的横截面积是10平方米。
学以致用
4.一条水渠长800米,横截面如下图。
(2)水渠水深2米,水在水渠中每分流动20米,该水渠每时的水流量是多少立方米?
4×2.5×20×60=12000(立方米)
答:该水渠每时的水流量是12000立方米。
学以致用
5.学校修建花园需要40吨沙,这堆沙够用吗?(每立方米沙重1.8吨。)
底面周长12.56米。
高1.2米。
这节课,我们复面图形和立体图形的特征和相关的知识,你掌握了吗?
课堂小结
