沪科版数学七年级下8.3完全平方公式与平方差公式(第1课时,完全平方公式)课件(共26张PPT)
文档属性
| 名称 | 沪科版数学七年级下8.3完全平方公式与平方差公式(第1课时,完全平方公式)课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 676.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 00:00:00 | ||
图片预览




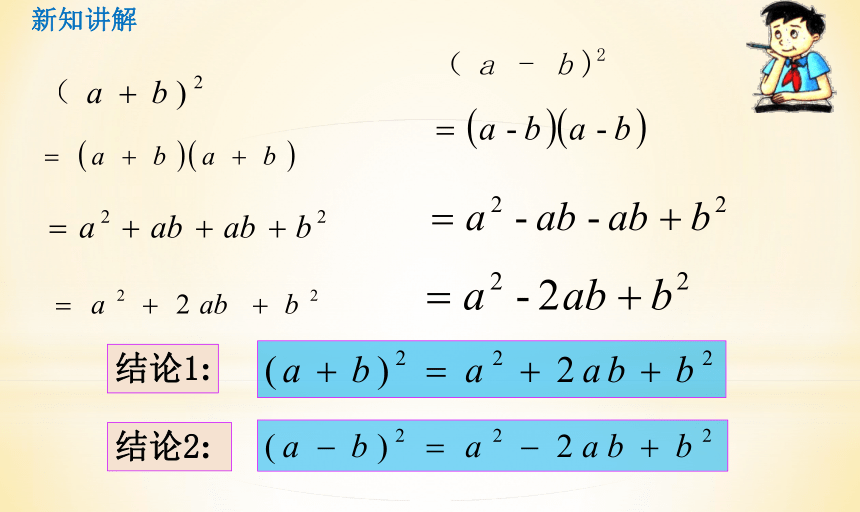


文档简介
(共26张PPT)
8.3完全平方公式与平方差公式
第一课时 完全平方公式
沪科版数学七年级下
1、多项式乘以多项式的 依据是什么?
2、如何进行多项式与多项式乘法运算?
3、 运用多项式乘法法则,要有序地逐项相乘,不要漏乘,并注意项的符号.
4、最后的计算结果要化简 ̄ ̄ ̄
合并同类项.
(m+b)(n+a)=
mn
+ ma
+ bn
+ ba
知识回顾
——分配率
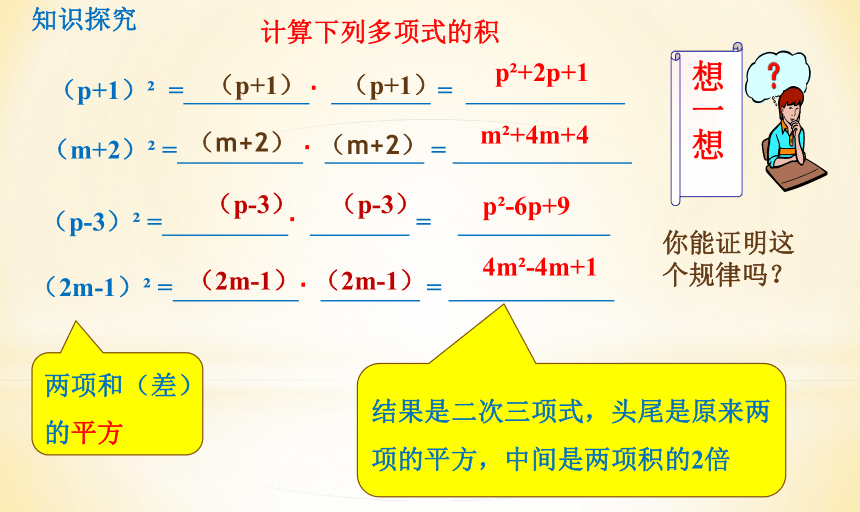
计算下列多项式的积
知识回顾
(p+1) = =
(m+2) = =
(2m-1) = =
(p-3) = =
p +2p+1
(p+1)
(p+1)
(m+2)
(m+2)
m +4m+4
(p-3)
(p-3)
p -6p+9
(2m-1)
(2m-1)
4m -4m+1
计算下列多项式的积
知识回顾
(p+1) = =
(m+2) = =
(2m-1) = =
(p-3) = =
p +2p+1
(p+1)
(p+1)
(m+2)
(m+2)
m +4m+4
(p-3)
(p-3)
p -6p+9
(2m-1)
(2m-1)
4m -4m+1
想一想
需要计算的算式有什么特征?
结果是几项式,有什么特征?
你能发现计算规律吗?
计算下列多项式的积
知识探究
(p+1) = =
(m+2) = =
(2m-1) = =
(p-3) = =
p +2p+1
(p+1)
(p+1)
(m+2)
(m+2)
m +4m+4
(p-3)
(p-3)
p -6p+9
(2m-1)
(2m-1)
4m -4m+1
想一想
两项和(差)的平方
结果是二次三项式,头尾是原来两项的平方,中间是两项积的2倍
你能证明这个规律吗?
新知讲解
结论1:
结论2:
完全平方公式
两数和的平方,等于这两数的平方和加上这两数积的两倍。
你能用语言描述这两个公式吗?
两数差的平方,等于这两数的平方和,减去这两数的积的两倍。
新知讲解
b
b
a
a
(a+b)
a
b
ab
ab
+
+
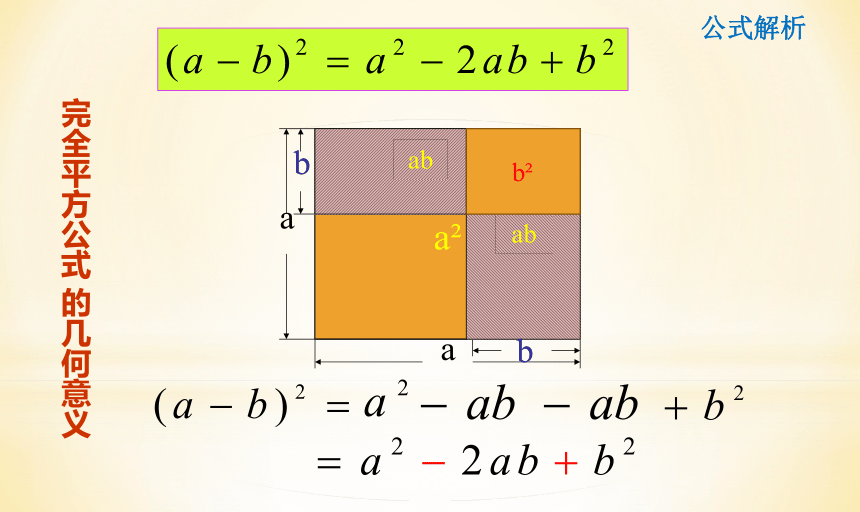
完全平方公式 的几何意义
公式解析
a
a
b
b
(a-b)
a
ab
ab
b
b
完全平方公式 的几何意义
b
公式解析
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
完全平方公式
首平方,尾平方,首尾两倍中间放
(首±尾)2=首2±2×首×尾+尾2
公式特征:
注意:1、积为二次三项式;
2、公式中的字母a,b不仅可以表示数,单个字母,也可以表示单项式或多项式.
公式解析
( x + 2y)2=
计算: (x+2y)2
( a + b)2=a2 + 2 a b + b2
x2
+
2· x ·2y
+
(2y)2
=x2 + 4xy+4y2
公式理解
解:
( x - 2y )2 =
计算: (x -2 y)2
( a - b)2=a2 - 2 a b + b2
x2
-
2· x ·2y
+
(2y)2
=x2 - 4xy+4y2
公式理解
解:
例1.运用完全平方公式计算:
(1)(4a-b)2 (2)(y+ )2
解:1) (4a-b)2 = (4a)2-2·4a·b+b2
= 16a2-8ab+b2
2) (y+ )2
= y2+y+
=y2+2·y· +( )2
(3)(x+2y)2; (4)(2a-5)2
(3)原式=x2+2·x·2y+(2y)2
=x2+4xy+4y2
(4)原式=(2a)2-2·2a·5+52
=4a2-20a+25
注意每一项系数
公式应用
(2)(-2x-1)2 =[-(2x+1)]2
=(2x+1)2
= (2x)2+2·2x·1+1
=4x2+4x+1
例2.运用完全平方公式计算:
(1)(-2s+t)2 (2) (-2x-1)2
例题讲解
注意每一项的符号与公式中“+”、“-”的意义区别
(2)(-2x-1)2
=[(-2x)-1)]2
= (-2x)2-2·(-2x)·1+1
=4x2+4x+1
解:
(1) (-2s+t)2
=(-2s)2+2(-2s)t+t2
=4s2-4st+t2
(1)(-2s+t)2= (t-2s)
= t -2·2s·t +(2s)2
=t2-4st+4s2
1.下面各式的计算结果是否正确?如果不正确,应当怎样改正?
错
错
错
错
(x +y)2 =x2+2xy +y2
(x -y)2 =x2 -2xy +y2
(x -y)2 =x2 -2xy +y2
(x +y)2 =x2+2xy +y2
(x+y)2=x2 +y2
(2)(x -y)2 =x2 -y2
(3) (x -y)2 =x2+2xy +y2
(4) (x+y)2 =x2 +xy +y2
公式辨析
(2) (a - b)2 与 (b - a)2
(1) (-a -b)2 与(a+b)2
2、比较下列各式之间的关系:
相等
相等
(3)(-b +a)2 与(-a +b)2
相等
互为相反数的两式的完全平方结果一样。
公式辨析
例3:利用完全平方公式计算:
(1) 0.982 (2) 10012
解:(1) 原式 = ( 1 0.02)2
= 12 2 ×1×0.02 + 0.022
= 1 0.04 + 0.0004
= 0.9604
(2)原式 = ( 1000 + 1 )2
= 10002 + 2 × 1000×1 + 12
= 1000000 + 2000 + 1
=1002001
例4、要给一边长为a米的正方形桌子辅上正方形的桌布,桌布的四周均超出桌面0.1米,问需要多大面积的桌布.
解:由题意知,桌布是边长为(a+0.2)米的正方形,故面积为:
(a+0.2 )2
= a2 +0.4a+0.04(平方米)
答:所需桌布的面积为a2 +0.4a+0.04(平方米)
公式应用
巩固练习
(1)
(2)
(3)
(4)
(5)
(6)
思考: (1)完全平方展开有几项?
(2)每一项的符号特征?
相信你能行
1、计算:
课堂练习:
(3)(-2a-3y)
解:
(3)(-2a-3y) =( 2a+3y ) =4a +12ay+9y
三项组合为两相和
运用完全平方公式计算:
1) 1022 2) 1992 3) 4982 4) 79.82
1) 1022=(100+2)2
=1002+2×100×2+22
= 10000+400+4 =10404
2) 1992 = (200-1)2
= 2002-2×200×1+12
= 40000-200+1 =39801
提升练习
3) 4982 = (500-2)2
= 5002-2×500×2+22
= 250000-2000+4 = 248004
4)79.82 = (80-0.2)2
=802-2×80×0.2+0.22
= 6400-32+0.04
= 6368.04
解:
拓展练习:
1. 2022 -2×2022×2021+2021 =_______;
2.若x +2kx+9 是一个完全平方公式,则k=_______
1
3.若 x +8x+k 是一个完全平方公式,则 k= _______;
=(2022-2-21)
x +2kx+9= x +2kx+(±3)
x +8x+k = x + 2.x.4 + k
4、知(a+b)2=11,ab=1,求(a-b)2的值.
解:
∴(a-b)2
=a -2ab+b
=a +b -2ab
=9-2
=7
∵(a+b)2=11
∴a +2ab+b =11
∵ab=1
∴a +b
=11-2×1
=9
∴a +b =11-2ab
整体代换
课堂小结: 完全平方公式
口诀:首平方,尾平方,首尾两倍中间放
在解题过程中要准确确定a和b、对照公式原形的两边, 做到不丢项、不弄错符号、2ab时不少乘2;
8.3完全平方公式与平方差公式
第一课时 完全平方公式
沪科版数学七年级下
1、多项式乘以多项式的 依据是什么?
2、如何进行多项式与多项式乘法运算?
3、 运用多项式乘法法则,要有序地逐项相乘,不要漏乘,并注意项的符号.
4、最后的计算结果要化简 ̄ ̄ ̄
合并同类项.
(m+b)(n+a)=
mn
+ ma
+ bn
+ ba
知识回顾
——分配率
计算下列多项式的积
知识回顾
(p+1) = =
(m+2) = =
(2m-1) = =
(p-3) = =
p +2p+1
(p+1)
(p+1)
(m+2)
(m+2)
m +4m+4
(p-3)
(p-3)
p -6p+9
(2m-1)
(2m-1)
4m -4m+1
计算下列多项式的积
知识回顾
(p+1) = =
(m+2) = =
(2m-1) = =
(p-3) = =
p +2p+1
(p+1)
(p+1)
(m+2)
(m+2)
m +4m+4
(p-3)
(p-3)
p -6p+9
(2m-1)
(2m-1)
4m -4m+1
想一想
需要计算的算式有什么特征?
结果是几项式,有什么特征?
你能发现计算规律吗?
计算下列多项式的积
知识探究
(p+1) = =
(m+2) = =
(2m-1) = =
(p-3) = =
p +2p+1
(p+1)
(p+1)
(m+2)
(m+2)
m +4m+4
(p-3)
(p-3)
p -6p+9
(2m-1)
(2m-1)
4m -4m+1
想一想
两项和(差)的平方
结果是二次三项式,头尾是原来两项的平方,中间是两项积的2倍
你能证明这个规律吗?
新知讲解
结论1:
结论2:
完全平方公式
两数和的平方,等于这两数的平方和加上这两数积的两倍。
你能用语言描述这两个公式吗?
两数差的平方,等于这两数的平方和,减去这两数的积的两倍。
新知讲解
b
b
a
a
(a+b)
a
b
ab
ab
+
+
完全平方公式 的几何意义
公式解析
a
a
b
b
(a-b)
a
ab
ab
b
b
完全平方公式 的几何意义
b
公式解析
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
完全平方公式
首平方,尾平方,首尾两倍中间放
(首±尾)2=首2±2×首×尾+尾2
公式特征:
注意:1、积为二次三项式;
2、公式中的字母a,b不仅可以表示数,单个字母,也可以表示单项式或多项式.
公式解析
( x + 2y)2=
计算: (x+2y)2
( a + b)2=a2 + 2 a b + b2
x2
+
2· x ·2y
+
(2y)2
=x2 + 4xy+4y2
公式理解
解:
( x - 2y )2 =
计算: (x -2 y)2
( a - b)2=a2 - 2 a b + b2
x2
-
2· x ·2y
+
(2y)2
=x2 - 4xy+4y2
公式理解
解:
例1.运用完全平方公式计算:
(1)(4a-b)2 (2)(y+ )2
解:1) (4a-b)2 = (4a)2-2·4a·b+b2
= 16a2-8ab+b2
2) (y+ )2
= y2+y+
=y2+2·y· +( )2
(3)(x+2y)2; (4)(2a-5)2
(3)原式=x2+2·x·2y+(2y)2
=x2+4xy+4y2
(4)原式=(2a)2-2·2a·5+52
=4a2-20a+25
注意每一项系数
公式应用
(2)(-2x-1)2 =[-(2x+1)]2
=(2x+1)2
= (2x)2+2·2x·1+1
=4x2+4x+1
例2.运用完全平方公式计算:
(1)(-2s+t)2 (2) (-2x-1)2
例题讲解
注意每一项的符号与公式中“+”、“-”的意义区别
(2)(-2x-1)2
=[(-2x)-1)]2
= (-2x)2-2·(-2x)·1+1
=4x2+4x+1
解:
(1) (-2s+t)2
=(-2s)2+2(-2s)t+t2
=4s2-4st+t2
(1)(-2s+t)2= (t-2s)
= t -2·2s·t +(2s)2
=t2-4st+4s2
1.下面各式的计算结果是否正确?如果不正确,应当怎样改正?
错
错
错
错
(x +y)2 =x2+2xy +y2
(x -y)2 =x2 -2xy +y2
(x -y)2 =x2 -2xy +y2
(x +y)2 =x2+2xy +y2
(x+y)2=x2 +y2
(2)(x -y)2 =x2 -y2
(3) (x -y)2 =x2+2xy +y2
(4) (x+y)2 =x2 +xy +y2
公式辨析
(2) (a - b)2 与 (b - a)2
(1) (-a -b)2 与(a+b)2
2、比较下列各式之间的关系:
相等
相等
(3)(-b +a)2 与(-a +b)2
相等
互为相反数的两式的完全平方结果一样。
公式辨析
例3:利用完全平方公式计算:
(1) 0.982 (2) 10012
解:(1) 原式 = ( 1 0.02)2
= 12 2 ×1×0.02 + 0.022
= 1 0.04 + 0.0004
= 0.9604
(2)原式 = ( 1000 + 1 )2
= 10002 + 2 × 1000×1 + 12
= 1000000 + 2000 + 1
=1002001
例4、要给一边长为a米的正方形桌子辅上正方形的桌布,桌布的四周均超出桌面0.1米,问需要多大面积的桌布.
解:由题意知,桌布是边长为(a+0.2)米的正方形,故面积为:
(a+0.2 )2
= a2 +0.4a+0.04(平方米)
答:所需桌布的面积为a2 +0.4a+0.04(平方米)
公式应用
巩固练习
(1)
(2)
(3)
(4)
(5)
(6)
思考: (1)完全平方展开有几项?
(2)每一项的符号特征?
相信你能行
1、计算:
课堂练习:
(3)(-2a-3y)
解:
(3)(-2a-3y) =( 2a+3y ) =4a +12ay+9y
三项组合为两相和
运用完全平方公式计算:
1) 1022 2) 1992 3) 4982 4) 79.82
1) 1022=(100+2)2
=1002+2×100×2+22
= 10000+400+4 =10404
2) 1992 = (200-1)2
= 2002-2×200×1+12
= 40000-200+1 =39801
提升练习
3) 4982 = (500-2)2
= 5002-2×500×2+22
= 250000-2000+4 = 248004
4)79.82 = (80-0.2)2
=802-2×80×0.2+0.22
= 6400-32+0.04
= 6368.04
解:
拓展练习:
1. 2022 -2×2022×2021+2021 =_______;
2.若x +2kx+9 是一个完全平方公式,则k=_______
1
3.若 x +8x+k 是一个完全平方公式,则 k= _______;
=(2022-2-21)
x +2kx+9= x +2kx+(±3)
x +8x+k = x + 2.x.4 + k
4、知(a+b)2=11,ab=1,求(a-b)2的值.
解:
∴(a-b)2
=a -2ab+b
=a +b -2ab
=9-2
=7
∵(a+b)2=11
∴a +2ab+b =11
∵ab=1
∴a +b
=11-2×1
=9
∴a +b =11-2ab
整体代换
课堂小结: 完全平方公式
口诀:首平方,尾平方,首尾两倍中间放
在解题过程中要准确确定a和b、对照公式原形的两边, 做到不丢项、不弄错符号、2ab时不少乘2;
