19.2.2 第2课时一次函数解析式的求法 课件(共19页)
文档属性
| 名称 | 19.2.2 第2课时一次函数解析式的求法 课件(共19页) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-27 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
人教版八下数学
精品同步教学课件
19.2.2 一次函数
第2课时 一次函数解析式的求法
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础水平的学生使用。课件包括以下环节:
新知引入
典例分析
自主学习
随堂练习
拓展提高
课堂小结
备选习题
前面,我们学习了一次函数及其图象和性质,你能写出两个具体的一次函数解析式吗?如何画出它们的图象?
思考:
反过来,已知一个一次函数的图象经过两个具体的点,你能求出它的解析式吗?
两点法——两点确定一条直线
问题引入
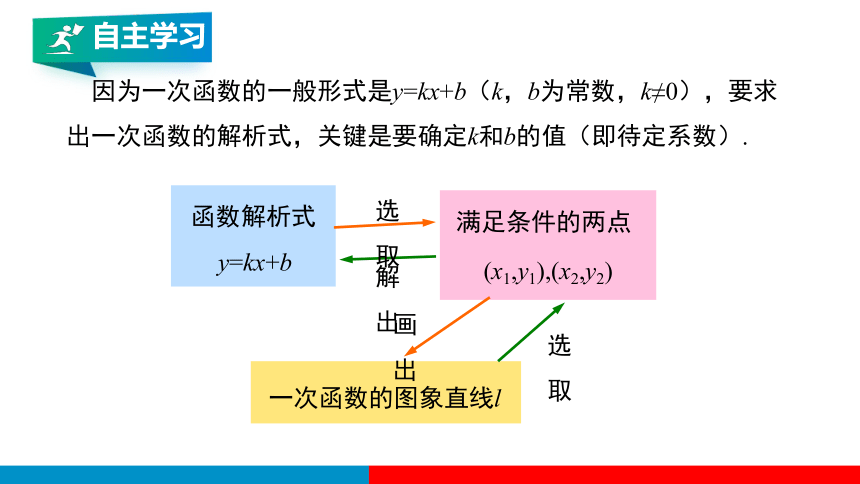
因为一次函数的一般形式是y=kx+b(k,b为常数,k≠0),要求出一次函数的解析式,关键是要确定k和b的值(即待定系数).
函数解析式
y=kx+b
满足条件的两点
(x1,y1),(x2,y2)
一次函数的图象直线l
选取
解出
画出
选取
自主学习
例 1
已知一次函数的图象过点(3, 5)与(-4,-9),求这个一次函数的解析式.
求一次函数y=kx+b的解析式,关 键是求出k,b的值.
从已知条件可以列出关于k,b的二元一次方程组,并求
出k,b.
分析:
设这个一次函数的解析式为y=kx+b(k≠0).
因为y=kx+b的图象过点(3, 5)与(-4,-9),
所以 解方程组得
这个一次函数的解析式为y=2x-1.
解:
典例分析
(1)设:设一次函数的一般形式 ;
(2)列:把图象上的点 , 代入一次函数的解析式,组成_________方程组;
(3)解:解二元一次方程组得k,b;
(4)还原:把k,b的值代入一次函数的解析式.
求一次函数解析式的步骤:
y=kx+b(k≠0)
二元一次
自主学习
1.
已知一次函数的图象经过点(9,0)和点(24,20),
写出函数解析式.
设一次函数解析式为y=kx+b.
则 解得
所以一次函数解析式为y= x-12.
解:
课堂练习
2.
若一次函数y=kx+b的图象经过点(0,2)和(1,0),则这个函数的解析式是( )
A.y=2x+3 B.y=3x+2
C.y=x+2 D.y=-2x+2
D
课堂练习
用图形变换法求一次函数的解析式
2
已知一次函数y=kx+b的图象经过点(-2,5),并且与y轴交于点P.直线y= 与y轴交于点Q,点Q恰与点P关于x轴对称.求这个一次函数的解析式.
要确定这个一次函数的解析式,关键是求出点P的
坐标.
导引:
例2
典例分析
∵点Q是直线 y= 与y轴的交点,
∴点Q的坐标为(0,3).
又∵点P与点Q关于x轴对称,
∴点P的坐标为(0,-3).
∴直线y=kx+b过(-2,5),(0,-3)两点,
∴这个一次函数的解析式为y=-4x-3.
解:
典例分析
归 纳
用待定系数法确定函数解析式时,应注意结合
题目信息,根据不同情况选择相应方法:
(1)如果已知图象经过点的坐标,那么可直接构造方
程(组)求解;
(2)当直线经过的点的坐标未知时,结合题意,先确
定直线经过的点的坐标,再构造方程(组)求解.
自主学习
1.
【中考·湖州】已知y是x的一次函数,当x=3时,y=1;当x=-2时,y=-4.求这个一次函数的解析式.
设这个一次函数的解析式为y=kx+b(k≠0),
将x=3,y=1和x=-2,y=-4分别代入上式
得 解得
所以这个一次函数的解析式为y=x-2.
解:
课堂练习
2.
已知y+2与x-1成正比例,且当x=3时,y=4.
(1)求y与x之间的函数解析式;
(2)当y=1时,求x的值.
(1)设y+2=k(x-1)(k≠0),把x=3,y=4代入,
得4+2=k(3-1),解得k=3.
则y与x之间的函数解析式是y+2=3(x-1),
即y=3x-5.
(2)当y=1时,3x-5=1,解得x=2.
解:
课堂练习
3.
根据下列条件,分别确定y关于x的函数解析式.
(1)y与x成正比例,且当x=9时,y=16;
(2)已知一次函数y=kx+b,当x=3时,y=2;
当x=-2时,y=1.
(1)设y=k′x(k′≠0),把x=9,y=16代入,
得16=9k′,k′= ,所以y= x.
解:
课堂练习
(2)把x=3,y=2和x=-2,y=1分别代入y=kx+b,
得 解得
所以y= x+ .
课堂练习
一次函数解
析式的求法
1.具备条件:一次函数y=kx+b中有两个不确定的系
数k,b,需要两个独立的条件确定两个关于k,b的
方程,求得k,b的值.这两个条件通常是两个点的
坐标或两对x,y的值.
2.确定方法:将两对已知变量的对应值分别代入
y=kx+b中,建立关于k,b的两个方程,通过解这
两个方程,求出k,b,从而确定其解析式.
课堂小结
一次函数解
析式的求法
用待定系数法求一次函数解析式的步骤:
(1)设:设解析式为y=kx+b;
(2)代:将已知的值代入所设的解析式, 得到关于k,
b的方程;
(3)解:解方程组求k,b的值;
(4)写:将k,b的值代回解析式中.并写出解析式.
课堂小结
https://www.21cnjy.com/help/help_extract.php
人教版八下数学
精品同步教学课件
19.2.2 一次函数
第2课时 一次函数解析式的求法
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础水平的学生使用。课件包括以下环节:
新知引入
典例分析
自主学习
随堂练习
拓展提高
课堂小结
备选习题
前面,我们学习了一次函数及其图象和性质,你能写出两个具体的一次函数解析式吗?如何画出它们的图象?
思考:
反过来,已知一个一次函数的图象经过两个具体的点,你能求出它的解析式吗?
两点法——两点确定一条直线
问题引入
因为一次函数的一般形式是y=kx+b(k,b为常数,k≠0),要求出一次函数的解析式,关键是要确定k和b的值(即待定系数).
函数解析式
y=kx+b
满足条件的两点
(x1,y1),(x2,y2)
一次函数的图象直线l
选取
解出
画出
选取
自主学习
例 1
已知一次函数的图象过点(3, 5)与(-4,-9),求这个一次函数的解析式.
求一次函数y=kx+b的解析式,关 键是求出k,b的值.
从已知条件可以列出关于k,b的二元一次方程组,并求
出k,b.
分析:
设这个一次函数的解析式为y=kx+b(k≠0).
因为y=kx+b的图象过点(3, 5)与(-4,-9),
所以 解方程组得
这个一次函数的解析式为y=2x-1.
解:
典例分析
(1)设:设一次函数的一般形式 ;
(2)列:把图象上的点 , 代入一次函数的解析式,组成_________方程组;
(3)解:解二元一次方程组得k,b;
(4)还原:把k,b的值代入一次函数的解析式.
求一次函数解析式的步骤:
y=kx+b(k≠0)
二元一次
自主学习
1.
已知一次函数的图象经过点(9,0)和点(24,20),
写出函数解析式.
设一次函数解析式为y=kx+b.
则 解得
所以一次函数解析式为y= x-12.
解:
课堂练习
2.
若一次函数y=kx+b的图象经过点(0,2)和(1,0),则这个函数的解析式是( )
A.y=2x+3 B.y=3x+2
C.y=x+2 D.y=-2x+2
D
课堂练习
用图形变换法求一次函数的解析式
2
已知一次函数y=kx+b的图象经过点(-2,5),并且与y轴交于点P.直线y= 与y轴交于点Q,点Q恰与点P关于x轴对称.求这个一次函数的解析式.
要确定这个一次函数的解析式,关键是求出点P的
坐标.
导引:
例2
典例分析
∵点Q是直线 y= 与y轴的交点,
∴点Q的坐标为(0,3).
又∵点P与点Q关于x轴对称,
∴点P的坐标为(0,-3).
∴直线y=kx+b过(-2,5),(0,-3)两点,
∴这个一次函数的解析式为y=-4x-3.
解:
典例分析
归 纳
用待定系数法确定函数解析式时,应注意结合
题目信息,根据不同情况选择相应方法:
(1)如果已知图象经过点的坐标,那么可直接构造方
程(组)求解;
(2)当直线经过的点的坐标未知时,结合题意,先确
定直线经过的点的坐标,再构造方程(组)求解.
自主学习
1.
【中考·湖州】已知y是x的一次函数,当x=3时,y=1;当x=-2时,y=-4.求这个一次函数的解析式.
设这个一次函数的解析式为y=kx+b(k≠0),
将x=3,y=1和x=-2,y=-4分别代入上式
得 解得
所以这个一次函数的解析式为y=x-2.
解:
课堂练习
2.
已知y+2与x-1成正比例,且当x=3时,y=4.
(1)求y与x之间的函数解析式;
(2)当y=1时,求x的值.
(1)设y+2=k(x-1)(k≠0),把x=3,y=4代入,
得4+2=k(3-1),解得k=3.
则y与x之间的函数解析式是y+2=3(x-1),
即y=3x-5.
(2)当y=1时,3x-5=1,解得x=2.
解:
课堂练习
3.
根据下列条件,分别确定y关于x的函数解析式.
(1)y与x成正比例,且当x=9时,y=16;
(2)已知一次函数y=kx+b,当x=3时,y=2;
当x=-2时,y=1.
(1)设y=k′x(k′≠0),把x=9,y=16代入,
得16=9k′,k′= ,所以y= x.
解:
课堂练习
(2)把x=3,y=2和x=-2,y=1分别代入y=kx+b,
得 解得
所以y= x+ .
课堂练习
一次函数解
析式的求法
1.具备条件:一次函数y=kx+b中有两个不确定的系
数k,b,需要两个独立的条件确定两个关于k,b的
方程,求得k,b的值.这两个条件通常是两个点的
坐标或两对x,y的值.
2.确定方法:将两对已知变量的对应值分别代入
y=kx+b中,建立关于k,b的两个方程,通过解这
两个方程,求出k,b,从而确定其解析式.
课堂小结
一次函数解
析式的求法
用待定系数法求一次函数解析式的步骤:
(1)设:设解析式为y=kx+b;
(2)代:将已知的值代入所设的解析式, 得到关于k,
b的方程;
(3)解:解方程组求k,b的值;
(4)写:将k,b的值代回解析式中.并写出解析式.
课堂小结
https://www.21cnjy.com/help/help_extract.php
