19.2.2 第3课时一次函数图象的应用 课件(共22页)
文档属性
| 名称 | 19.2.2 第3课时一次函数图象的应用 课件(共22页) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-27 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
人教版八下数学
精品同步教学课件
19.2.2 一次函数
第3课时 一次函数图象的应用
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础水平的学生使用。课件包括以下环节:
新知引入
典例分析
自主学习
随堂练习
拓展提高
课堂小结
备选习题
从数量关系中获取信息的应用
1
1.利用函数方法解决实际问题,关键是分析题中的
数量关系,联系实际生活及以前学过的内容,将
实际问题抽象、升华为一次函数模型,即建模,
再利用函数的性质解决问题.一次函数的应用主
要有两种类型:
自主学习
(1)给出了一次函数关系式,直接应用一次函数的
性质解决问题;
(2)只用语言叙述或用表格、图象提供一次函数的
情境时,应先求出关系式,进而利用函数性质
解决问题.
自主学习
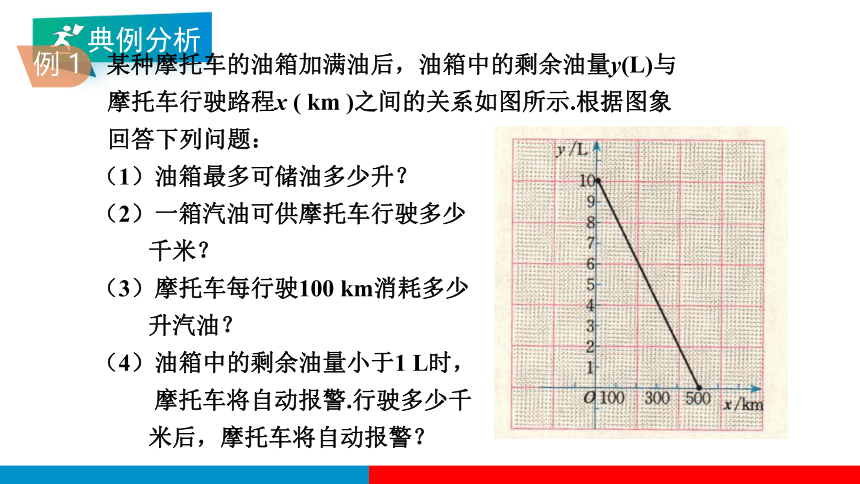
例 1
某种摩托车的油箱加满油后,油箱中的剩余油量y(L)与
摩托车行驶路程x ( km )之间的关系如图所示.根据图象
回答下列问题:
(1)油箱最多可储油多少升?
(2)一箱汽油可供摩托车行驶多少
千米?
(3)摩托车每行驶100 km消耗多少
升汽油?
(4)油箱中的剩余油量小于1 L时,
摩托车将自动报警.行驶多少千
米后,摩托车将自动报警?
典例分析
解:观察图象,得
(1)当x = 0时,y=10.因此,油箱最多可储油10L.
(2)当y = 0时,x = 500.因此,一箱汽油可供摩托车行
驶500 km.
(3) x从0增加到100时,y从10减少到8,减少了 2,因此
摩托车每行驶100 km消耗2 L汽油.
当y=1时, x= 450.因此,行驶450km后,摩托车将
自动报警.
典例分析
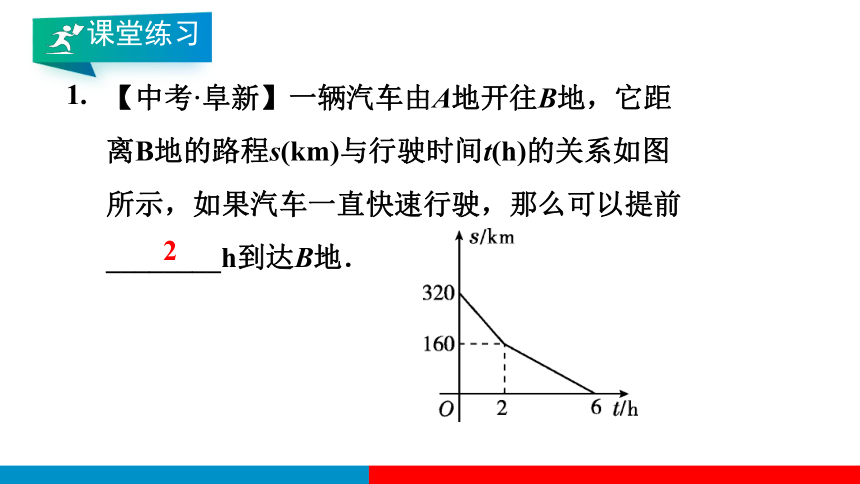
1.
【中考·阜新】一辆汽车由A地开往B地,它距离B地的路程s(km)与行驶时间t(h)的关系如图所示,如果汽车一直快速行驶,那么可以提前________h到达B地.
2
课堂练习
例2
某移动公司采用分段计费的方法
来计算话费,月通话时间x(min)
与相应话费y(元)之间的函数图象
如图.
(1)分别求出当0≤x<100和x≥100
时,y与x之间的函数解析式.
(2)月通话为280 min时,应交话费多少元?
从图像中获取信息的应用
2
典例分析
(1)当0≤x<100时,设y1=k1x(k1≠0),
将(100,40)代入得100k1=40,解得k1=
所以正比例函数的解析式为
当x≥100时,设y2=k2x+b(k2≠0),
将(100,40)及(200,60)分别代入得
所以一次函数解析式为
解:
典例分析
因为280>100,
所以将x=280代入 中,得
即月通话时间为280 min时,应交话费76元.
解:
(2)月通话为280 min时,应交话费多少元?
典例分析
购买种子 数量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额/元 …
例3 “黄金1号”玉米种子的价格为5 元/kg,如果一次购买2 kg 以上的种子,超过2 kg 部分的种子的价格打8 折.
(1)填写下表:
2.5
5
7.5
10
12
14
16
18
典例分析
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
分析:从题目可知,种子的价格与 有关.
若购买种子量为x>2时,种子价格y为:
.
若购买种子量为0≤x≤2时,种子价格y为: .
购买种子量
y=5x
y=4(x-2)+10=4x+2
典例分析
解:设购买量为x千克,付款金额为y元.
当x>2时,y=4(x-2)+10=4x+2.
当0≤x≤2时,y=5x;
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
叫做分段函数.
注意:1.它是一个函数;
2.要写明自变量取值范围.
y =
5x(0≤x≤2)
4x+2(x>2)
{
典例分析
y=5x(0≤x≤2)
y=4x+2(x>2)
y
x
O
1
2
10
3
14
的函数图象为:
y =
5x(0≤x≤2)
4x+2(x>2)
{
典例分析
思考:
你能由上面的函数解析式或函数图象解决以下问题吗?
(1)一次购买1.5 kg 种子,需付款多少元?
(2)30元最多能购买多少种子?
典例分析
归 纳
分段函数中,自变量在不同的取值范围内的解
析式不同,在解决问题时,要特别注意自变量的取
值范围的变化.分段函数的应用面广,在水费、电
费、商品促销等领域都有广泛应用.本题考查一次
函数及识图能力,体现了数形结合思想.解决问题
的关键是由图象挖掘出有用的信息,利用待定系数
法先求出函数解析式,再解决问题.
1.
【中考·哈尔滨】明君社区有一块空地需要绿化,
某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
A.300 m2 B.150 m2
C.330 m2 D.450 m2
B
课堂练习
某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(小时)的变化情况如图所示,当成年人按规定剂量服药后.
(1)服药后______小时,血液中含药量最高,达到每毫升_______毫克,接着逐步衰弱.
(2)服药5小时,血液中含药量为
每毫升____毫克.
x/小时
y/毫克
6
3
2
5
O
2
6
3
拓展提升
(3)当x≤2时y与x之间的函数解析式是___________.
(4)当x≥2时y与x之间的函数解析式是___________.
(5)如果每毫升血液中含药量3毫克或3毫克以上时,治疗疾病最有效,那么这个有效时间是______小时.
y=3x
y=-x+8
4
x/小时
y/毫克
6
3
2
5
O
拓展提升
一次函数图象的应用
运用一次函数解决实际问题的方法:
在日常生活和生产实践中有不少问题的数量关系可以
用一次函数来刻画.在运用一次函数解决实际问题时,
首先判断问题中的两个变量之间是不是一次函数关系,
当确定是一次函数关系时,求出函数解析式,并运用
一次函数的图象和性质进一步求得所需的结果.
课堂小结
https://www.21cnjy.com/help/help_extract.php
人教版八下数学
精品同步教学课件
19.2.2 一次函数
第3课时 一次函数图象的应用
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础水平的学生使用。课件包括以下环节:
新知引入
典例分析
自主学习
随堂练习
拓展提高
课堂小结
备选习题
从数量关系中获取信息的应用
1
1.利用函数方法解决实际问题,关键是分析题中的
数量关系,联系实际生活及以前学过的内容,将
实际问题抽象、升华为一次函数模型,即建模,
再利用函数的性质解决问题.一次函数的应用主
要有两种类型:
自主学习
(1)给出了一次函数关系式,直接应用一次函数的
性质解决问题;
(2)只用语言叙述或用表格、图象提供一次函数的
情境时,应先求出关系式,进而利用函数性质
解决问题.
自主学习
例 1
某种摩托车的油箱加满油后,油箱中的剩余油量y(L)与
摩托车行驶路程x ( km )之间的关系如图所示.根据图象
回答下列问题:
(1)油箱最多可储油多少升?
(2)一箱汽油可供摩托车行驶多少
千米?
(3)摩托车每行驶100 km消耗多少
升汽油?
(4)油箱中的剩余油量小于1 L时,
摩托车将自动报警.行驶多少千
米后,摩托车将自动报警?
典例分析
解:观察图象,得
(1)当x = 0时,y=10.因此,油箱最多可储油10L.
(2)当y = 0时,x = 500.因此,一箱汽油可供摩托车行
驶500 km.
(3) x从0增加到100时,y从10减少到8,减少了 2,因此
摩托车每行驶100 km消耗2 L汽油.
当y=1时, x= 450.因此,行驶450km后,摩托车将
自动报警.
典例分析
1.
【中考·阜新】一辆汽车由A地开往B地,它距离B地的路程s(km)与行驶时间t(h)的关系如图所示,如果汽车一直快速行驶,那么可以提前________h到达B地.
2
课堂练习
例2
某移动公司采用分段计费的方法
来计算话费,月通话时间x(min)
与相应话费y(元)之间的函数图象
如图.
(1)分别求出当0≤x<100和x≥100
时,y与x之间的函数解析式.
(2)月通话为280 min时,应交话费多少元?
从图像中获取信息的应用
2
典例分析
(1)当0≤x<100时,设y1=k1x(k1≠0),
将(100,40)代入得100k1=40,解得k1=
所以正比例函数的解析式为
当x≥100时,设y2=k2x+b(k2≠0),
将(100,40)及(200,60)分别代入得
所以一次函数解析式为
解:
典例分析
因为280>100,
所以将x=280代入 中,得
即月通话时间为280 min时,应交话费76元.
解:
(2)月通话为280 min时,应交话费多少元?
典例分析
购买种子 数量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额/元 …
例3 “黄金1号”玉米种子的价格为5 元/kg,如果一次购买2 kg 以上的种子,超过2 kg 部分的种子的价格打8 折.
(1)填写下表:
2.5
5
7.5
10
12
14
16
18
典例分析
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
分析:从题目可知,种子的价格与 有关.
若购买种子量为x>2时,种子价格y为:
.
若购买种子量为0≤x≤2时,种子价格y为: .
购买种子量
y=5x
y=4(x-2)+10=4x+2
典例分析
解:设购买量为x千克,付款金额为y元.
当x>2时,y=4(x-2)+10=4x+2.
当0≤x≤2时,y=5x;
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
叫做分段函数.
注意:1.它是一个函数;
2.要写明自变量取值范围.
y =
5x(0≤x≤2)
4x+2(x>2)
{
典例分析
y=5x(0≤x≤2)
y=4x+2(x>2)
y
x
O
1
2
10
3
14
的函数图象为:
y =
5x(0≤x≤2)
4x+2(x>2)
{
典例分析
思考:
你能由上面的函数解析式或函数图象解决以下问题吗?
(1)一次购买1.5 kg 种子,需付款多少元?
(2)30元最多能购买多少种子?
典例分析
归 纳
分段函数中,自变量在不同的取值范围内的解
析式不同,在解决问题时,要特别注意自变量的取
值范围的变化.分段函数的应用面广,在水费、电
费、商品促销等领域都有广泛应用.本题考查一次
函数及识图能力,体现了数形结合思想.解决问题
的关键是由图象挖掘出有用的信息,利用待定系数
法先求出函数解析式,再解决问题.
1.
【中考·哈尔滨】明君社区有一块空地需要绿化,
某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
A.300 m2 B.150 m2
C.330 m2 D.450 m2
B
课堂练习
某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(小时)的变化情况如图所示,当成年人按规定剂量服药后.
(1)服药后______小时,血液中含药量最高,达到每毫升_______毫克,接着逐步衰弱.
(2)服药5小时,血液中含药量为
每毫升____毫克.
x/小时
y/毫克
6
3
2
5
O
2
6
3
拓展提升
(3)当x≤2时y与x之间的函数解析式是___________.
(4)当x≥2时y与x之间的函数解析式是___________.
(5)如果每毫升血液中含药量3毫克或3毫克以上时,治疗疾病最有效,那么这个有效时间是______小时.
y=3x
y=-x+8
4
x/小时
y/毫克
6
3
2
5
O
拓展提升
一次函数图象的应用
运用一次函数解决实际问题的方法:
在日常生活和生产实践中有不少问题的数量关系可以
用一次函数来刻画.在运用一次函数解决实际问题时,
首先判断问题中的两个变量之间是不是一次函数关系,
当确定是一次函数关系时,求出函数解析式,并运用
一次函数的图象和性质进一步求得所需的结果.
课堂小结
https://www.21cnjy.com/help/help_extract.php
