人教版六年级数学下册 6.4.1 数学思考(1) 上课课件(共26张PPT)
文档属性
| 名称 | 人教版六年级数学下册 6.4.1 数学思考(1) 上课课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
整理和复习
6
4. 数学思考
第1课时 数学思考(1)
人教版六年级数学下册 上课课件
学习目标
1.使学生通过画图,由简到繁,发现规律,总结规律,进一步巩固、发展学生找规律的能力,体会找规律对解决问题的重要性。
2.体会一些数学思想、方法在解决问题中的作用,掌握一些数学思想和数学方法,会用一些数学思想和方法解决生活中的问题。
3.进一步体验充满着探索与创造的数学活动,激发学生学习数学、探索规律的兴趣。
学习重点 难点
学生通过画图,由简到繁,发现规律,总结规律。
1、根据数的变化规律填数。
13、11、9、( )、( )、( )。
2、根据珠子的排列规律,接着画出。
7
5
3
3、1+2+3+4+5+6+……15+16+17+18+19+20 =
210
( 1 + 20 ) ×20 ÷ 2 = 210
你是怎么算的?还有更简便的算法吗?
( 1 + 20 ) ×20 ÷ 2 = 210
(首数+尾数)×个数÷2
同学们,课前我们来做一个游戏吧,请你们拿出纸和笔在纸上任意点上8个点,并将它们每两点连成一条线,再数一数,看看连成了多少条线段。
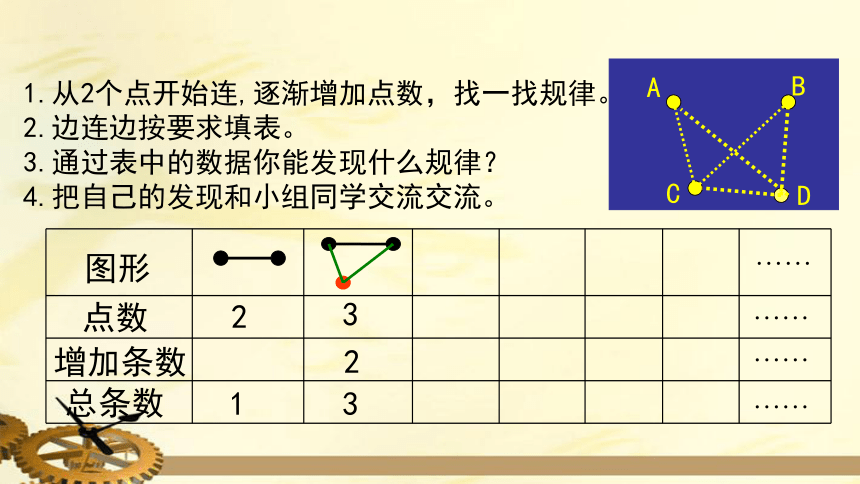
1.从2个点开始连,逐渐增加点数,找一找规律。
2.边连边按要求填表。
3.通过表中的数据你能发现什么规律?
4.把自己的发现和小组同学交流交流。
A
B
C
D
图形
点数
增加条数
总条数
2
1
3
2
3
……
……
……
……
C
D
A
B
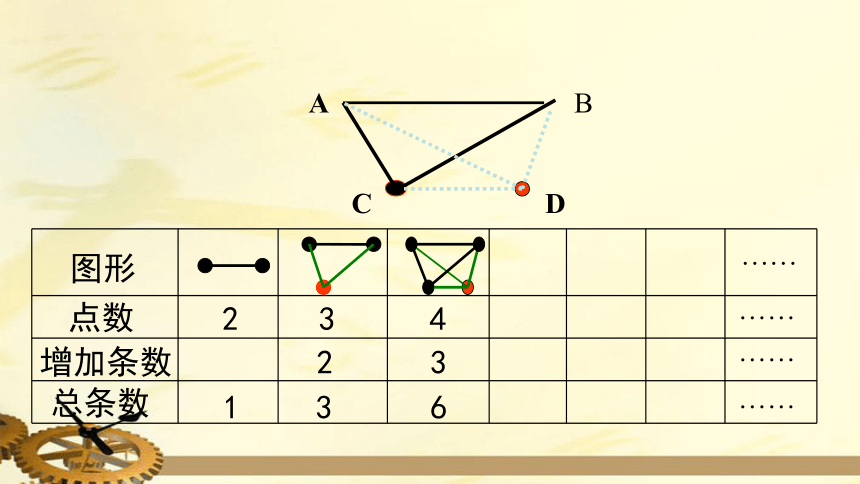
图形
点数
增加条数
总条数
……
……
……
……
2
1
3
2
3
4
3
6
2
1
3
2
3
4
3
6
5
4
10
A
B
C
D
图形
点数
增加条数
总条数
……
……
……
……
2
1
3
2
3
4
3
6
5
4
10
6
5
15
A
B
C
D
图形
点数
增加条数
总条数
……
……
……
……
仔细观察表格,你能发现哪些信息 有什么规律?
2
1
3
2
3
4
3
6
5
4
10
6
5
15
1 + 2 + 3 + 4 + 5 + 6 + …… +(点数— 1)= 总条数
点数×(点数-1) ÷ 2 = 总条数
点数×增加条数÷2=总条数
7
6
21
图形
点数
增加条数
总条数
……
……
……
……
考虑到重复的线段,会得到什么结论?
A
E
D
C
B
5
×
(5-1)
÷2
=10
我们用5个点来探讨以上规律。
n ×(n-1) ÷2 即:点数×(点数-1)÷2
=(1+11)+(2+10)+(3+9)+(4+8)
+(5+7)+6
问题:按照简单的方法计算,你发现了什么?
1+2+3+4+5+6+7+8+9+10+11
=66(条)……12个点
=12×5+6
根据规律,你知道12个点、20个点能连多少条线段吗?
1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19
=(1+19)+(2+18)+(3+17)
+……+(8+12)+(9+11)+10
=20×9+10
=190(条)……20个点
根据规律,你知道12个点、20个点能连多少条线段吗?
同学们,在我们生活中有许多看似复杂的问题,我们都可以尝试从简单问题去思考,逐步找到其中的规律,从而来解决复杂的问题。
想一想 算一算:
寒假过去了,10个好朋友见面了,每两位好朋友握手一次,请同学们帮忙算算,他们一共握了多少次手?
1+2+3+4+5+6+7+8+9=45(次)
答:一共握了45次手。
10×(10 - 1)÷2=45(次)
(1+9)×9÷2=45(次)
摆一摆,找一找。
1、第6个图形是什么图形?
2、摆第7个图形需要用多少根小棒?
答:第六个图形是平形四边形
答: 2 × 7 + 1 = 15 (根)
------
------
------
多边形
边数
内角和
3
4
5
6
720
1、多边形内角和与它的边数有什么关系?
2、一个九边形的内角和是多少度?
看表格观察思考:
180
360
540
180
×
( n - 2 ) = 多边形内角和
180
×
(9-2) = 1260°
问题:1. 你想怎样解决这个问题?
2. 从最简单的数据开始,数一数每幅图各有多少个棋子?
3. 在数的过程中,你发现了什么?
每行的棋子数×行数=棋子总数
1×1 2×2 3×3 4×4
1 4 9 16
观察下图,想一想。
(1)第7幅图有多少个棋子?第15幅图呢?
问题:1. 第7幅图每行有几个棋子?有几行?共有几个棋子?
3. 第15幅图共有几个棋子?
7×7=49(个)
15×15=225(个)
2. 每边的棋子数与图形的序号有什么关系?
观察下图,想一想。
(1)第7幅图有多少个棋子?第15幅图呢?
观察下图,想一想。
(2)第n幅图有多少个棋子?
问题:第n幅图每边有多少个棋子?一共有多少个棋子?
每行的棋子数×行数=棋子总数
n×n=棋子总数
n2=棋子总数
问题:遇到复杂的问题,你可以怎样思考?
3. 有序思考
2. 画图、枚举
1. 化繁为简
4. 探究规律
为迎接学校运动会,昨天下午校领导15人到会场开会。开会前,两两进行握手,问一共可以握手几次?
15× ( 15-1) ÷ 2 = 105 (次)
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
整理和复习
6
4. 数学思考
第1课时 数学思考(1)
人教版六年级数学下册 上课课件
学习目标
1.使学生通过画图,由简到繁,发现规律,总结规律,进一步巩固、发展学生找规律的能力,体会找规律对解决问题的重要性。
2.体会一些数学思想、方法在解决问题中的作用,掌握一些数学思想和数学方法,会用一些数学思想和方法解决生活中的问题。
3.进一步体验充满着探索与创造的数学活动,激发学生学习数学、探索规律的兴趣。
学习重点 难点
学生通过画图,由简到繁,发现规律,总结规律。
1、根据数的变化规律填数。
13、11、9、( )、( )、( )。
2、根据珠子的排列规律,接着画出。
7
5
3
3、1+2+3+4+5+6+……15+16+17+18+19+20 =
210
( 1 + 20 ) ×20 ÷ 2 = 210
你是怎么算的?还有更简便的算法吗?
( 1 + 20 ) ×20 ÷ 2 = 210
(首数+尾数)×个数÷2
同学们,课前我们来做一个游戏吧,请你们拿出纸和笔在纸上任意点上8个点,并将它们每两点连成一条线,再数一数,看看连成了多少条线段。
1.从2个点开始连,逐渐增加点数,找一找规律。
2.边连边按要求填表。
3.通过表中的数据你能发现什么规律?
4.把自己的发现和小组同学交流交流。
A
B
C
D
图形
点数
增加条数
总条数
2
1
3
2
3
……
……
……
……
C
D
A
B
图形
点数
增加条数
总条数
……
……
……
……
2
1
3
2
3
4
3
6
2
1
3
2
3
4
3
6
5
4
10
A
B
C
D
图形
点数
增加条数
总条数
……
……
……
……
2
1
3
2
3
4
3
6
5
4
10
6
5
15
A
B
C
D
图形
点数
增加条数
总条数
……
……
……
……
仔细观察表格,你能发现哪些信息 有什么规律?
2
1
3
2
3
4
3
6
5
4
10
6
5
15
1 + 2 + 3 + 4 + 5 + 6 + …… +(点数— 1)= 总条数
点数×(点数-1) ÷ 2 = 总条数
点数×增加条数÷2=总条数
7
6
21
图形
点数
增加条数
总条数
……
……
……
……
考虑到重复的线段,会得到什么结论?
A
E
D
C
B
5
×
(5-1)
÷2
=10
我们用5个点来探讨以上规律。
n ×(n-1) ÷2 即:点数×(点数-1)÷2
=(1+11)+(2+10)+(3+9)+(4+8)
+(5+7)+6
问题:按照简单的方法计算,你发现了什么?
1+2+3+4+5+6+7+8+9+10+11
=66(条)……12个点
=12×5+6
根据规律,你知道12个点、20个点能连多少条线段吗?
1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19
=(1+19)+(2+18)+(3+17)
+……+(8+12)+(9+11)+10
=20×9+10
=190(条)……20个点
根据规律,你知道12个点、20个点能连多少条线段吗?
同学们,在我们生活中有许多看似复杂的问题,我们都可以尝试从简单问题去思考,逐步找到其中的规律,从而来解决复杂的问题。
想一想 算一算:
寒假过去了,10个好朋友见面了,每两位好朋友握手一次,请同学们帮忙算算,他们一共握了多少次手?
1+2+3+4+5+6+7+8+9=45(次)
答:一共握了45次手。
10×(10 - 1)÷2=45(次)
(1+9)×9÷2=45(次)
摆一摆,找一找。
1、第6个图形是什么图形?
2、摆第7个图形需要用多少根小棒?
答:第六个图形是平形四边形
答: 2 × 7 + 1 = 15 (根)
------
------
------
多边形
边数
内角和
3
4
5
6
720
1、多边形内角和与它的边数有什么关系?
2、一个九边形的内角和是多少度?
看表格观察思考:
180
360
540
180
×
( n - 2 ) = 多边形内角和
180
×
(9-2) = 1260°
问题:1. 你想怎样解决这个问题?
2. 从最简单的数据开始,数一数每幅图各有多少个棋子?
3. 在数的过程中,你发现了什么?
每行的棋子数×行数=棋子总数
1×1 2×2 3×3 4×4
1 4 9 16
观察下图,想一想。
(1)第7幅图有多少个棋子?第15幅图呢?
问题:1. 第7幅图每行有几个棋子?有几行?共有几个棋子?
3. 第15幅图共有几个棋子?
7×7=49(个)
15×15=225(个)
2. 每边的棋子数与图形的序号有什么关系?
观察下图,想一想。
(1)第7幅图有多少个棋子?第15幅图呢?
观察下图,想一想。
(2)第n幅图有多少个棋子?
问题:第n幅图每边有多少个棋子?一共有多少个棋子?
每行的棋子数×行数=棋子总数
n×n=棋子总数
n2=棋子总数
问题:遇到复杂的问题,你可以怎样思考?
3. 有序思考
2. 画图、枚举
1. 化繁为简
4. 探究规律
为迎接学校运动会,昨天下午校领导15人到会场开会。开会前,两两进行握手,问一共可以握手几次?
15× ( 15-1) ÷ 2 = 105 (次)
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
