第十章 概率章末综合练习-2021-2022学年高一下学期数学人教A版(2019)必修第二册(word版含解析)
文档属性
| 名称 | 第十章 概率章末综合练习-2021-2022学年高一下学期数学人教A版(2019)必修第二册(word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 498.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 00:00:00 | ||
图片预览




文档简介
第十章 概率 章末综合练习
一、单选题
1.抛掷两枚均匀的骰子,记录正面朝上的点数,则下列选项的两个事件中,互斥但不对立的是( )
A.事件“点数之和为奇数”与事件“点数之和为9”
B.事件“点数之和为偶数”与事件“点数之和为奇数”
C.事件“点数之和为6”与事件“点数之和为9”
D.事件“点数之和不小于9”与事件“点数之和小于等于8”
2.5张卡片上分别写有数字0,1,2,3,4,从中任意抽取一张,抽到的卡片上的数字为奇数的概率是( )
A. B.
C. D.
3.某社区防疫志愿者中有2人的工作是负责测量体温,有3人的工作是负责查验行程码.若则这5人中任选2人参加优秀志愿者评选,则选取的2人负责不同工作的概率为( )
A. B. C. D.
4.某大学的“篮球”“无人机”“戏剧”三个社团考核挑选新社员,已知大一某新生对这三个社团都很感兴趣,决定三个考核都参加,假设他通过“篮球”“无人机”“戏剧”三个社团考核的概率依次为、、,且他通过每个考核相互独立,若三个社团考核他都能通过的概率为,至少通过一个社团考核的概率为,则( )
A. B. C. D.
5.先后次抛掷一枚骰子,将得到的点数分别记为、,两次点数互不影响,设三条线段的长分别为、和,求这三条线段能围成等腰三角形(含等边三角形)的概率为( )
A. B. C. D.
6.甲乙两队进行羽毛球决赛,甲队只要再胜一局就获得冠军,乙队需要再胜两局才能获得冠军,若每局甲队获胜的概率为,则甲队获得冠军的概率为( )
A. B. C. D.
7.已知集合,.从集合A中任取一个元素m,则的概率为( )
A. B. C. D.
8.米接力赛是田径运动中的集体项目.一根小小的木棒,要四个人共同打造一个信念,一起拼搏,每次交接都是信任的传递.甲 乙 丙 丁四位同学将代表高一年级参加校运会米接力赛,教练组根据训练情况,安排了四人的交接棒组合.已知该组合三次交接棒失误的概率分别是,,,假设三次交接棒相互独立,则此次比赛中该组合交接棒没有失误的概率是( )
A. B.
C. D.
二、多选题
9.甲、乙两人做游戏,下列游戏中公平的是( )
A.抛一枚骰子,向上的点数为奇数则甲胜,向上的点数为偶数则乙胜
B.同时抛两枚相同的骰子,向上的点数之和大于7则甲胜,否则乙胜
C.从一副不含大、小王的扑克牌中抽一张,扑克牌是红色则甲胜,是黑色则乙胜
D.甲、乙两人各写一个数字,若是同奇或同偶则甲胜,否则乙胜
10.对于事件,,下列命题正确的是 ( )
A.如果,互斥,那么与也互斥
B.如果,对立,那么与也对立
C.如果,独立,那么与也独立
D.如果,不独立,那么与也不独立
11.已知事件A,B相互独立,且,,则( )
A. B.
C. D.
12.从甲袋中摸出一个红球的概率是,从乙袋中摸出一个红球的概率是,从两袋各摸出一个球,下列结论正确的是( )
A.2个球都是红球的概率为 B.2个球中恰有1个红球的概率为
C.至少有1个红球的概率为 D.2个球不都是红球的概率为
三、填空题
13.现从3男3女共6名学生中随机抽取2人进行座谈,则这2人中至少有一名女生的概率为___________.
14.已知甲、乙、丙三人去参加某公司面试,他们被该公司录取的概率分别是,且三人录取结果相互之间没有影响,则他们三人中恰有两人被录取的概率为_
15.甲、乙两校共有5名教师报名支援边远贫困地区教育,其中甲校2男1女,乙校1男1女,现选出2名教师去支援边远贫困地区教育,则选出的2名教师来自同一学校的概率为______.
16.高一(11)班班主任准备安排A,B,C三位同学参与某一周的班级值日工作,其中周一周二安排一位同学,周三周四安排一位同学,周五安排一位同学,周六周日不安排,则A同学周三在值日的可能性是___________.
四、解答题
17.从0,1,2这3个数字中,不放回地取两次,每次取一个,构成数对,x为第一次取到的数字,y为第二次取到的数字.
(1)写出这个试验的样本空间;
(2)求出这个试验基本事件的总数;
(3)写出“第一次取出的数字是2”这一事件.
18.某电视台要招聘两名播音员,现在有三名符合条件的女士和两名符合条件的男士前来应聘,如果每个应聘人员被录用的概率相同,计算下列事件的概率:
(1)一名男士和一名女士被录用;
(2)两名男士被录用;
(3)两名女士被录用.
19.袋中装有质地均匀的红、白色球各一个,每次任取一个,有放回地抽取三次,写出所有的样本点,并计算下列事件的概率:
(1)三次中恰有两个球同色;
(2)三次抽取的球颜色相同;
(3)三次抽取的球中红色球出现的次数多于白色球出现的次数.
20.甲、乙两人玩射击游戏,甲、乙射击命中与否是相互独立事件.规则如下:若射击一次命中,则原射击人继续射击;若射击一次不中,就由对方接替射击,已知甲、乙两人射击一次命中的概率均为,且第一次由甲开始射击.
(1)求前3次射击中甲恰好命中2次的概率;
(2)求第4次由甲射击的概率.
21.2022年新冠肺炎仍在世界好多国家肆虐,尽管我国抗疫取得了很大的成绩,疫情也得到了很好的遏制,但由于整个国际环境的影响,时而也会出现一些散发病例,故而抗疫形势依然艰巨.我市某小区为了防止疫情在小区出现,严防外来人员进入小区,切实保障居民正常生活,设置“特殊值班岗”.现有包含甲、乙在内的4名志愿者参与该工作,每人安排一天,每4天一轮.在一轮的“特殊值班岗”安排中,求:
(1)甲、乙两人相邻值班的概率;
(2)甲或乙被安排在前2天值班的概率.
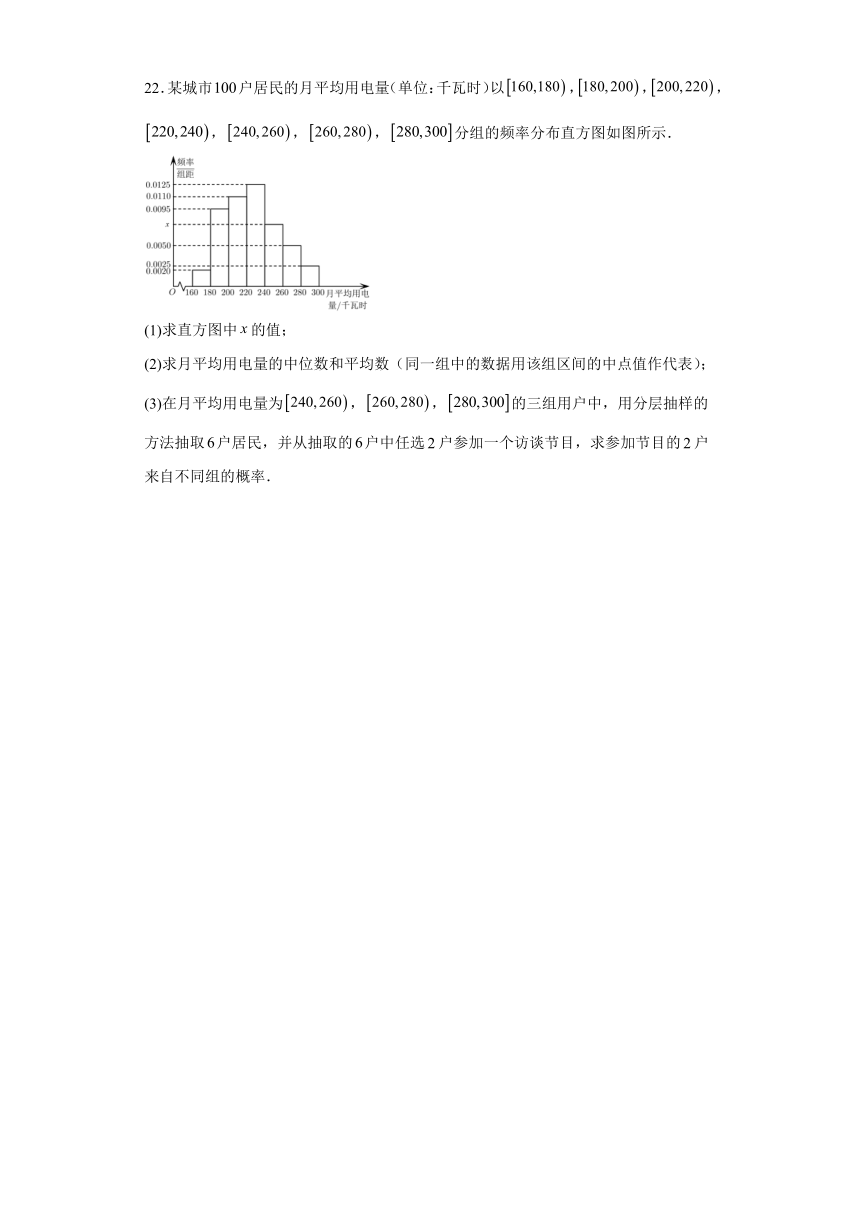
22.某城市户居民的月平均用电量(单位:千瓦时)以,,,,,,分组的频率分布直方图如图所示.
(1)求直方图中的值;
(2)求月平均用电量的中位数和平均数(同一组中的数据用该组区间的中点值作代表);
(3)在月平均用电量为,,的三组用户中,用分层抽样的方法抽取户居民,并从抽取的户中任选户参加一个访谈节目,求参加节目的户来自不同组的概率.
试卷第1页,共3页
参考答案:
1.C
【解析】对于,二者能同时发生,不是互斥事件,故错误;
对于,二者不能同时发生,也不能同时不发生,是对立事件,故错误;
对于,二者不能同时发生,但能同时不发生,是互斥但不对立事件,故正确;
对于,二者不能同时发生,也不能同时不发生,是对立事件,故错误.
故选:.
2.C
【解析】5张卡片中卡片上的数字为奇数的有张,从中任意抽取一张,抽到的卡片上的数字为奇数的概率是;故选:C
3.C
【解析】设负责测量体温的志愿者分别为,负责查验行程码的志愿者分别为,
则从中选2人的情况有,共10种,
其中2人负责不同工作的情况有,共6种,所以所求概率.
故选:C
4.D
【解析】因为三个社团考核他都能通过的概率为,至少通过一个社团考核的概率为,
所以,即,解得.故选: D.
5.B
【解析】先后次抛掷一枚骰子,将得到的点数分别记为、,以为一个基本事件,所有的基本事件个数为,
其中,“三条线段的长分别为、和,这三条线段能围成等腰三角形(含等边三角形)”所包含的基本事件有:、、、、、、、、、、,共个,故所求事件的概率为.故选:B.
6.D
【解析】由已知得甲对获胜可能以下分为两种情况:
①第一局甲队获胜,此时的概率为;
②第一局乙队获胜,第二局甲队获胜,此时的概率为,
综上所述,甲队获胜的概率为,故选:D.
7.B
【解析】集合A中的元素有共7个元素,
其中属于集合的有共3个元素,
故从集合A中任取一个元素m,则的概率为.故选:B
8.C
【解析】由题意,三次交接棒不失误的概率分别为:,则该组合不失误的概率为:.故选:C.
9.ACD
【解析】对于选项A,甲胜和乙胜的概率都是,所以游戏是公平的;
对于选项B,点数之和大于7和点数之和小于7的概率相等,但点数等于7时乙胜,所以甲胜的概率小,所以游戏不公平;
对于选项C,甲胜和乙胜的概率都是,所以游戏是公平的;
对于选项D,甲胜的概率是,乙胜的概率是,所以游戏是公平的.
故选:ACD
10.BCD
【解析】A.如果,互斥,由互斥事件的定义得与不一定互斥,故错误;
B.如果,对立,由对立事件的定义得与也对立,故正确;
C.如果,独立,由相互独立事件的定义得与也独立,故正确;
D.如果,不独立,由相互独立事件的定义得与也不独立,故正确;
故答案为:BCD
11.ACD
【解析】∵事件A,B相互独立,且,,
∴,故A正确;
,故B错误;
,故C正确;
,故D正确.
故选:ACD.
12.AB
【解析】记从甲袋中摸出一个红球的事件为A,从乙袋中摸出一个红球的事件为B,则,,A,B相互独立,
2个球都是红球的事件为AB,则有,A正确;
2个球中恰有1个红球的事件为,则,B正确;
至少有1个红球的事件的对立事件是,则,所以至少有1个红球的概率为,C不正确;
2个球不都是红球的事件是事件AB的对立事件,其概率为,D不正确.
故选:AB
13.【解析】记男生为,女生为,
从中任取人有:,共种方法.
其中至少有名女生的有:,共种,
所以这2人中至少有一名女生的概率为.
14.【解析】因为甲、乙、丙三人被该公司录取的概率分别是,且三人录取结果相互之间没有影响,甲和乙被录取的概率为,
甲和丙被录取的概率为,
乙和丙被录取的概率为
则他们三人中恰有两人被录取的概率为,
15.【解析】来自甲校的教师设为a,b,c,来自乙校的教师设为1,2,则全部情况为:,共有10种情况,其中4种符合要求,为,故选出的2名教师来自同一学校的概率为.
16.【解析】周一周二安排一位同学,周三周四安排一位同学,周五安排一位同学,周六周日不安排共有
周一周二,周三周四,周五;
周一周二,周三周四,周五;
周一周二,周三周四,周五;
周一周二,周三周四,周五;
周一周二,周三周四,周五;
周一周二,周三周四,周五,种方法,
其中A同学在周三值日有
周一周二,周三周四,周五;
周一周二,周三周四,周五,种方法,
则A同学周三在值日的可能性是.
17.【解析】(1)样本空间:;
(2)由(1)知基本事件总数为6.
(3)由(1)得:.
18.【解析】(1)记三名女播音员分别为A,B,C,两名男播音员分别为a,b,录用两名播音员的试验的不同结果:
AB,AC,Aa,Ab,BC,Ba,Bb,Ca,Cb,ab,共10个不同结果,它们等可能,
一名男士和一名女士被录用的事件M的不同结果为:Aa,Ab,Ba,Bb,Ca,Cb,共6个,,
所以一名男士和一名女士被录用的概率为.
(2)由(1)知,两名男士被录用的事件N的结果为:ab,有1个,,
所以两名男士被录用的概率为.
(3)由(1)知,两名女士被录用的事件Q的结果为:AB,AC,BC,共3个,,
所以两名女士被录用的概率为.
19.【解析】(1)袋中装有质地均匀的红、白色球各一个,每次任取一个,有放回地抽取三次,记整个事件空间为,则(红,红,红),(红,红,白),(红,白,红),(白,红,红),(红,白,白),(白,红,白),(白,白,红),(白,白,白),其中(红,白,红)表示第一次抽到红球,第二次抽到白球,第三次抽到红球,共有8个样本点
记三次中恰有两个球同色为事件,
则(红,红,白),(红,白,红),(白,红,红),(红,白,白),(白,红,白),(白,白,红),共有6个样本点
由古典概型的概率公式
(2)记三次抽取的球颜色相同为事件,
则(红,红,红),(白,白,白),共有2个样本点
由古典概型的概率公式
(3)记三次抽取的球中红色球出现的次数多于白色球出现的次数为事件,
则(红,红,红),(红,红,白),(红,白,红),(白,红,红),共有4个样本点
由古典概型的概率公式
20.【解析】(1)由题意,前3次射击中甲恰好击中2次,即前2次甲都击中目标,
但第3次没有击中目标,所以它的概率为.
(2)根据题意,分为4种情况:
第3次由甲射击包括甲连续射击3次且都击中;
第1次甲射击击中,但第2次没有击中,第3次由乙射击没有击中;
第1次甲射击没有击中,且乙射击第二次击中,但第3次没有击中;
第1次甲没有击中,且乙射击第2次没有击中,第3次甲射击击中,
所以这件事的概率为.
21.【解析】(1)由题意,设4名志愿者为甲,乙,丙,丁,4天一轮的值班安排所有可能的结果是:(甲,乙,丙,丁),(甲,乙,丁,丙),(甲,丙,乙,丁),(甲,丙,丁,乙),(甲,丁,乙,丙),(甲,丁,丙,乙),(乙,甲,丙,丁),(乙,甲丁,丙),
(乙,丙,甲,丁),(乙,丙,丁,甲),(乙,丁,甲,丙),(乙,丁,丙,甲),
(丙,甲,乙,丁),(丙,甲,丁,乙),(丙,乙,甲,丁),(丙,乙,丁,甲),
(丙,丁,乙,甲),(丙,丁,甲,乙),(丁,甲,乙,丙),(丁,甲,丙,乙),
(丁,乙,甲,丙),(丁,乙,丙,甲),(丁,丙,乙,甲),(丁,丙,甲,乙),
共24个样本点
设甲乙相邻为事件A,则事件A包含:(甲,乙,丙,丁),(甲,乙,丁,丙),
(乙,甲,丙,丁),(乙,甲,丁,丙),(丙,甲,乙,丁),(丙,乙,甲,丁),(丙,丁,乙,甲),(丙,丁,甲,乙),(丁,甲,乙,丙),(丁,乙,甲,丙),(丁,丙,乙,甲),(丁,丙,甲,乙),
共12个样本点,故
(2)设甲或乙被安排在前两天值班的为事件B.
则事件B包含:(甲,乙,丙,丁),(甲,乙,丁,丙),(甲,丙,乙,丁),(甲,丙,丁,乙),(甲,丁,乙,丙),(甲,丁,丙,乙),(乙,甲,丙,丁),(乙,甲,丁,丙),(乙,丙,甲,丁),(乙,丙,丁,甲),(乙,丁,甲,丙),(乙,丁,丙,甲),(丙,甲,乙,丁),(丙,甲,丁,乙),(丙,乙,甲,丁),(丙,乙,丁,甲),(丁,甲,乙,丙),(丁,甲,丙,乙),(丁,乙,甲,丙),(丁,乙,丙,甲),
共20个样本点,故.
22.【解析】(1)由,
得,所以直方图中的值是;
(2)中位数:因为,
且,
所以月平均用电量的中位数在内,设中位数为,由,解得,
所以月平均用电量的中位数是.
平均数:;
(3)月平均用电量在的用户有户,
月平均用电量在的用户有户,
月平均用电量在的用户有户.
抽样方法为分层抽样,在,,中的用户比为,
所以在,,中分别抽取户、户和户.
设参加节目的户来自不同组为事件,将来自的用户记为,,,来自的用户记为,,来自的用户记为,在户中随机抽取户,,
共包含个样本点,其中,包含的样本点个数为,
故参加节目的户来自不同组的概率.
答案第1页,共2页
一、单选题
1.抛掷两枚均匀的骰子,记录正面朝上的点数,则下列选项的两个事件中,互斥但不对立的是( )
A.事件“点数之和为奇数”与事件“点数之和为9”
B.事件“点数之和为偶数”与事件“点数之和为奇数”
C.事件“点数之和为6”与事件“点数之和为9”
D.事件“点数之和不小于9”与事件“点数之和小于等于8”
2.5张卡片上分别写有数字0,1,2,3,4,从中任意抽取一张,抽到的卡片上的数字为奇数的概率是( )
A. B.
C. D.
3.某社区防疫志愿者中有2人的工作是负责测量体温,有3人的工作是负责查验行程码.若则这5人中任选2人参加优秀志愿者评选,则选取的2人负责不同工作的概率为( )
A. B. C. D.
4.某大学的“篮球”“无人机”“戏剧”三个社团考核挑选新社员,已知大一某新生对这三个社团都很感兴趣,决定三个考核都参加,假设他通过“篮球”“无人机”“戏剧”三个社团考核的概率依次为、、,且他通过每个考核相互独立,若三个社团考核他都能通过的概率为,至少通过一个社团考核的概率为,则( )
A. B. C. D.
5.先后次抛掷一枚骰子,将得到的点数分别记为、,两次点数互不影响,设三条线段的长分别为、和,求这三条线段能围成等腰三角形(含等边三角形)的概率为( )
A. B. C. D.
6.甲乙两队进行羽毛球决赛,甲队只要再胜一局就获得冠军,乙队需要再胜两局才能获得冠军,若每局甲队获胜的概率为,则甲队获得冠军的概率为( )
A. B. C. D.
7.已知集合,.从集合A中任取一个元素m,则的概率为( )
A. B. C. D.
8.米接力赛是田径运动中的集体项目.一根小小的木棒,要四个人共同打造一个信念,一起拼搏,每次交接都是信任的传递.甲 乙 丙 丁四位同学将代表高一年级参加校运会米接力赛,教练组根据训练情况,安排了四人的交接棒组合.已知该组合三次交接棒失误的概率分别是,,,假设三次交接棒相互独立,则此次比赛中该组合交接棒没有失误的概率是( )
A. B.
C. D.
二、多选题
9.甲、乙两人做游戏,下列游戏中公平的是( )
A.抛一枚骰子,向上的点数为奇数则甲胜,向上的点数为偶数则乙胜
B.同时抛两枚相同的骰子,向上的点数之和大于7则甲胜,否则乙胜
C.从一副不含大、小王的扑克牌中抽一张,扑克牌是红色则甲胜,是黑色则乙胜
D.甲、乙两人各写一个数字,若是同奇或同偶则甲胜,否则乙胜
10.对于事件,,下列命题正确的是 ( )
A.如果,互斥,那么与也互斥
B.如果,对立,那么与也对立
C.如果,独立,那么与也独立
D.如果,不独立,那么与也不独立
11.已知事件A,B相互独立,且,,则( )
A. B.
C. D.
12.从甲袋中摸出一个红球的概率是,从乙袋中摸出一个红球的概率是,从两袋各摸出一个球,下列结论正确的是( )
A.2个球都是红球的概率为 B.2个球中恰有1个红球的概率为
C.至少有1个红球的概率为 D.2个球不都是红球的概率为
三、填空题
13.现从3男3女共6名学生中随机抽取2人进行座谈,则这2人中至少有一名女生的概率为___________.
14.已知甲、乙、丙三人去参加某公司面试,他们被该公司录取的概率分别是,且三人录取结果相互之间没有影响,则他们三人中恰有两人被录取的概率为_
15.甲、乙两校共有5名教师报名支援边远贫困地区教育,其中甲校2男1女,乙校1男1女,现选出2名教师去支援边远贫困地区教育,则选出的2名教师来自同一学校的概率为______.
16.高一(11)班班主任准备安排A,B,C三位同学参与某一周的班级值日工作,其中周一周二安排一位同学,周三周四安排一位同学,周五安排一位同学,周六周日不安排,则A同学周三在值日的可能性是___________.
四、解答题
17.从0,1,2这3个数字中,不放回地取两次,每次取一个,构成数对,x为第一次取到的数字,y为第二次取到的数字.
(1)写出这个试验的样本空间;
(2)求出这个试验基本事件的总数;
(3)写出“第一次取出的数字是2”这一事件.
18.某电视台要招聘两名播音员,现在有三名符合条件的女士和两名符合条件的男士前来应聘,如果每个应聘人员被录用的概率相同,计算下列事件的概率:
(1)一名男士和一名女士被录用;
(2)两名男士被录用;
(3)两名女士被录用.
19.袋中装有质地均匀的红、白色球各一个,每次任取一个,有放回地抽取三次,写出所有的样本点,并计算下列事件的概率:
(1)三次中恰有两个球同色;
(2)三次抽取的球颜色相同;
(3)三次抽取的球中红色球出现的次数多于白色球出现的次数.
20.甲、乙两人玩射击游戏,甲、乙射击命中与否是相互独立事件.规则如下:若射击一次命中,则原射击人继续射击;若射击一次不中,就由对方接替射击,已知甲、乙两人射击一次命中的概率均为,且第一次由甲开始射击.
(1)求前3次射击中甲恰好命中2次的概率;
(2)求第4次由甲射击的概率.
21.2022年新冠肺炎仍在世界好多国家肆虐,尽管我国抗疫取得了很大的成绩,疫情也得到了很好的遏制,但由于整个国际环境的影响,时而也会出现一些散发病例,故而抗疫形势依然艰巨.我市某小区为了防止疫情在小区出现,严防外来人员进入小区,切实保障居民正常生活,设置“特殊值班岗”.现有包含甲、乙在内的4名志愿者参与该工作,每人安排一天,每4天一轮.在一轮的“特殊值班岗”安排中,求:
(1)甲、乙两人相邻值班的概率;
(2)甲或乙被安排在前2天值班的概率.
22.某城市户居民的月平均用电量(单位:千瓦时)以,,,,,,分组的频率分布直方图如图所示.
(1)求直方图中的值;
(2)求月平均用电量的中位数和平均数(同一组中的数据用该组区间的中点值作代表);
(3)在月平均用电量为,,的三组用户中,用分层抽样的方法抽取户居民,并从抽取的户中任选户参加一个访谈节目,求参加节目的户来自不同组的概率.
试卷第1页,共3页
参考答案:
1.C
【解析】对于,二者能同时发生,不是互斥事件,故错误;
对于,二者不能同时发生,也不能同时不发生,是对立事件,故错误;
对于,二者不能同时发生,但能同时不发生,是互斥但不对立事件,故正确;
对于,二者不能同时发生,也不能同时不发生,是对立事件,故错误.
故选:.
2.C
【解析】5张卡片中卡片上的数字为奇数的有张,从中任意抽取一张,抽到的卡片上的数字为奇数的概率是;故选:C
3.C
【解析】设负责测量体温的志愿者分别为,负责查验行程码的志愿者分别为,
则从中选2人的情况有,共10种,
其中2人负责不同工作的情况有,共6种,所以所求概率.
故选:C
4.D
【解析】因为三个社团考核他都能通过的概率为,至少通过一个社团考核的概率为,
所以,即,解得.故选: D.
5.B
【解析】先后次抛掷一枚骰子,将得到的点数分别记为、,以为一个基本事件,所有的基本事件个数为,
其中,“三条线段的长分别为、和,这三条线段能围成等腰三角形(含等边三角形)”所包含的基本事件有:、、、、、、、、、、,共个,故所求事件的概率为.故选:B.
6.D
【解析】由已知得甲对获胜可能以下分为两种情况:
①第一局甲队获胜,此时的概率为;
②第一局乙队获胜,第二局甲队获胜,此时的概率为,
综上所述,甲队获胜的概率为,故选:D.
7.B
【解析】集合A中的元素有共7个元素,
其中属于集合的有共3个元素,
故从集合A中任取一个元素m,则的概率为.故选:B
8.C
【解析】由题意,三次交接棒不失误的概率分别为:,则该组合不失误的概率为:.故选:C.
9.ACD
【解析】对于选项A,甲胜和乙胜的概率都是,所以游戏是公平的;
对于选项B,点数之和大于7和点数之和小于7的概率相等,但点数等于7时乙胜,所以甲胜的概率小,所以游戏不公平;
对于选项C,甲胜和乙胜的概率都是,所以游戏是公平的;
对于选项D,甲胜的概率是,乙胜的概率是,所以游戏是公平的.
故选:ACD
10.BCD
【解析】A.如果,互斥,由互斥事件的定义得与不一定互斥,故错误;
B.如果,对立,由对立事件的定义得与也对立,故正确;
C.如果,独立,由相互独立事件的定义得与也独立,故正确;
D.如果,不独立,由相互独立事件的定义得与也不独立,故正确;
故答案为:BCD
11.ACD
【解析】∵事件A,B相互独立,且,,
∴,故A正确;
,故B错误;
,故C正确;
,故D正确.
故选:ACD.
12.AB
【解析】记从甲袋中摸出一个红球的事件为A,从乙袋中摸出一个红球的事件为B,则,,A,B相互独立,
2个球都是红球的事件为AB,则有,A正确;
2个球中恰有1个红球的事件为,则,B正确;
至少有1个红球的事件的对立事件是,则,所以至少有1个红球的概率为,C不正确;
2个球不都是红球的事件是事件AB的对立事件,其概率为,D不正确.
故选:AB
13.【解析】记男生为,女生为,
从中任取人有:,共种方法.
其中至少有名女生的有:,共种,
所以这2人中至少有一名女生的概率为.
14.【解析】因为甲、乙、丙三人被该公司录取的概率分别是,且三人录取结果相互之间没有影响,甲和乙被录取的概率为,
甲和丙被录取的概率为,
乙和丙被录取的概率为
则他们三人中恰有两人被录取的概率为,
15.【解析】来自甲校的教师设为a,b,c,来自乙校的教师设为1,2,则全部情况为:,共有10种情况,其中4种符合要求,为,故选出的2名教师来自同一学校的概率为.
16.【解析】周一周二安排一位同学,周三周四安排一位同学,周五安排一位同学,周六周日不安排共有
周一周二,周三周四,周五;
周一周二,周三周四,周五;
周一周二,周三周四,周五;
周一周二,周三周四,周五;
周一周二,周三周四,周五;
周一周二,周三周四,周五,种方法,
其中A同学在周三值日有
周一周二,周三周四,周五;
周一周二,周三周四,周五,种方法,
则A同学周三在值日的可能性是.
17.【解析】(1)样本空间:;
(2)由(1)知基本事件总数为6.
(3)由(1)得:.
18.【解析】(1)记三名女播音员分别为A,B,C,两名男播音员分别为a,b,录用两名播音员的试验的不同结果:
AB,AC,Aa,Ab,BC,Ba,Bb,Ca,Cb,ab,共10个不同结果,它们等可能,
一名男士和一名女士被录用的事件M的不同结果为:Aa,Ab,Ba,Bb,Ca,Cb,共6个,,
所以一名男士和一名女士被录用的概率为.
(2)由(1)知,两名男士被录用的事件N的结果为:ab,有1个,,
所以两名男士被录用的概率为.
(3)由(1)知,两名女士被录用的事件Q的结果为:AB,AC,BC,共3个,,
所以两名女士被录用的概率为.
19.【解析】(1)袋中装有质地均匀的红、白色球各一个,每次任取一个,有放回地抽取三次,记整个事件空间为,则(红,红,红),(红,红,白),(红,白,红),(白,红,红),(红,白,白),(白,红,白),(白,白,红),(白,白,白),其中(红,白,红)表示第一次抽到红球,第二次抽到白球,第三次抽到红球,共有8个样本点
记三次中恰有两个球同色为事件,
则(红,红,白),(红,白,红),(白,红,红),(红,白,白),(白,红,白),(白,白,红),共有6个样本点
由古典概型的概率公式
(2)记三次抽取的球颜色相同为事件,
则(红,红,红),(白,白,白),共有2个样本点
由古典概型的概率公式
(3)记三次抽取的球中红色球出现的次数多于白色球出现的次数为事件,
则(红,红,红),(红,红,白),(红,白,红),(白,红,红),共有4个样本点
由古典概型的概率公式
20.【解析】(1)由题意,前3次射击中甲恰好击中2次,即前2次甲都击中目标,
但第3次没有击中目标,所以它的概率为.
(2)根据题意,分为4种情况:
第3次由甲射击包括甲连续射击3次且都击中;
第1次甲射击击中,但第2次没有击中,第3次由乙射击没有击中;
第1次甲射击没有击中,且乙射击第二次击中,但第3次没有击中;
第1次甲没有击中,且乙射击第2次没有击中,第3次甲射击击中,
所以这件事的概率为.
21.【解析】(1)由题意,设4名志愿者为甲,乙,丙,丁,4天一轮的值班安排所有可能的结果是:(甲,乙,丙,丁),(甲,乙,丁,丙),(甲,丙,乙,丁),(甲,丙,丁,乙),(甲,丁,乙,丙),(甲,丁,丙,乙),(乙,甲,丙,丁),(乙,甲丁,丙),
(乙,丙,甲,丁),(乙,丙,丁,甲),(乙,丁,甲,丙),(乙,丁,丙,甲),
(丙,甲,乙,丁),(丙,甲,丁,乙),(丙,乙,甲,丁),(丙,乙,丁,甲),
(丙,丁,乙,甲),(丙,丁,甲,乙),(丁,甲,乙,丙),(丁,甲,丙,乙),
(丁,乙,甲,丙),(丁,乙,丙,甲),(丁,丙,乙,甲),(丁,丙,甲,乙),
共24个样本点
设甲乙相邻为事件A,则事件A包含:(甲,乙,丙,丁),(甲,乙,丁,丙),
(乙,甲,丙,丁),(乙,甲,丁,丙),(丙,甲,乙,丁),(丙,乙,甲,丁),(丙,丁,乙,甲),(丙,丁,甲,乙),(丁,甲,乙,丙),(丁,乙,甲,丙),(丁,丙,乙,甲),(丁,丙,甲,乙),
共12个样本点,故
(2)设甲或乙被安排在前两天值班的为事件B.
则事件B包含:(甲,乙,丙,丁),(甲,乙,丁,丙),(甲,丙,乙,丁),(甲,丙,丁,乙),(甲,丁,乙,丙),(甲,丁,丙,乙),(乙,甲,丙,丁),(乙,甲,丁,丙),(乙,丙,甲,丁),(乙,丙,丁,甲),(乙,丁,甲,丙),(乙,丁,丙,甲),(丙,甲,乙,丁),(丙,甲,丁,乙),(丙,乙,甲,丁),(丙,乙,丁,甲),(丁,甲,乙,丙),(丁,甲,丙,乙),(丁,乙,甲,丙),(丁,乙,丙,甲),
共20个样本点,故.
22.【解析】(1)由,
得,所以直方图中的值是;
(2)中位数:因为,
且,
所以月平均用电量的中位数在内,设中位数为,由,解得,
所以月平均用电量的中位数是.
平均数:;
(3)月平均用电量在的用户有户,
月平均用电量在的用户有户,
月平均用电量在的用户有户.
抽样方法为分层抽样,在,,中的用户比为,
所以在,,中分别抽取户、户和户.
设参加节目的户来自不同组为事件,将来自的用户记为,,,来自的用户记为,,来自的用户记为,在户中随机抽取户,,
共包含个样本点,其中,包含的样本点个数为,
故参加节目的户来自不同组的概率.
答案第1页,共2页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
