2022年华师大版九年级数学下册一课一练:26.2二次函数的图象与性质习题(Word版 含答案)
文档属性
| 名称 | 2022年华师大版九年级数学下册一课一练:26.2二次函数的图象与性质习题(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 200.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 00:00:00 | ||
图片预览



文档简介
26.2《二次函数的图象与性质》习题4
一、填空题
1.抛物线y=-x2+15有最______点,其坐标是______.
2.若抛物线y=x2-2x-2的顶点为A,与y轴的交点为B,则过A,B两点的直线的解析式为____________.
3.若抛物线y=ax2+bx+c(a≠0)的图象与抛物线y=x2-4x+3的图象关于y轴对称,则函数y=ax2+bx+c的解析式为______.
4.若抛物线y=x2+bx+c与y轴交于点A,与x轴正半轴交于B,C两点,且BC=2,S△ABC=3,则b=______.
5.二次函数y=x2-6x+c的图象的顶点与原点的距离为5,则c=______.
6.二次函数的图象在坐标平面内绕顶点旋转180°,再向左平移3个单位,向上平移5个单位后图象对应的二次函数解析式为_______.
二、选择题
7.把二次函数的图象向右平移2个单位后,再向上平移3个单位,所得的函数图象顶点是( )
A.(-5,1) B.(1,-5)
C.(-1,1) D.(-1,3)
8.若点(2,5),(4,5)在抛物线y=ax2+bx+c上,则它的对称轴是( )
A. B.x=1 C.x=2 D.x=3
9.已知函数,当函数值y随x的增大而减小时,x的取值范围是( )
A.x<1 B.x>1 C.x>-2 D.-2<x<4
10.二次函数y=a(x+k)2+k,当k取不同的实数值时,图象顶点所在的直线是( )
A.y=x B.x轴 C.y=-x D.y轴
11.图中有相同对称轴的两条抛物线,下列关系不正确的是( )
A.h=m B.k>n
C.k=n D.h>0,k>0
12.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①abc>0;②a+b+c=2;;④b<1.其中正确的结论是( )
A.①② B.②③
C.②④ D.③④
13.下列命题中,正确的是( )
①若a+b+c=0,则b2-4ac<0;
②若b=2a+3c,则一元二次方程ax2+bx+c=0有两个不相等的实数根;
③若b2-4ac>0,则二次函数y=ax2+bx+c的图象与坐标轴的公共点的个数是2或3;
④若b>a+c,则一元二次方程ax2+bx+c=0,有两个不相等的实数根.
A.②④ B.①③ C.②③ D.③④
三、解答题
14.把二次函数配方成y=a(x-k)2+h的形式,并求出它的图象的顶点坐标、对称轴方程,y<0时x的取值范围,并画出图象.
15.已知二次函数y=ax2+bx+c(a≠0)的图象经过一次函数的图象与x轴、y轴的交点,并也经过(1,1)点.求这个二次函数解析式,并求x为何值时,有最大(最小)值,这个值是什么
16.已知抛物线y=-x2+bx+c与x轴的两个交点分别为A(m,0),B(n,0),且,
(1)求此抛物线的解析式;
(2)设此抛物线与y轴的交点为C,过C作一条平行x轴的直线交抛物线于另一点P,求△ACP的面积.
17.已知抛物线y=ax2+bx+c经过点A(-1,0),且经过直线y=x-3与x轴的交点B及与y轴的交点C.
(1)求抛物线的解析式;
(2)求抛物线的顶点坐标;
(3)若点M在第四象限内的抛物线上,且OM⊥BC,垂足为D,求点M的坐标.
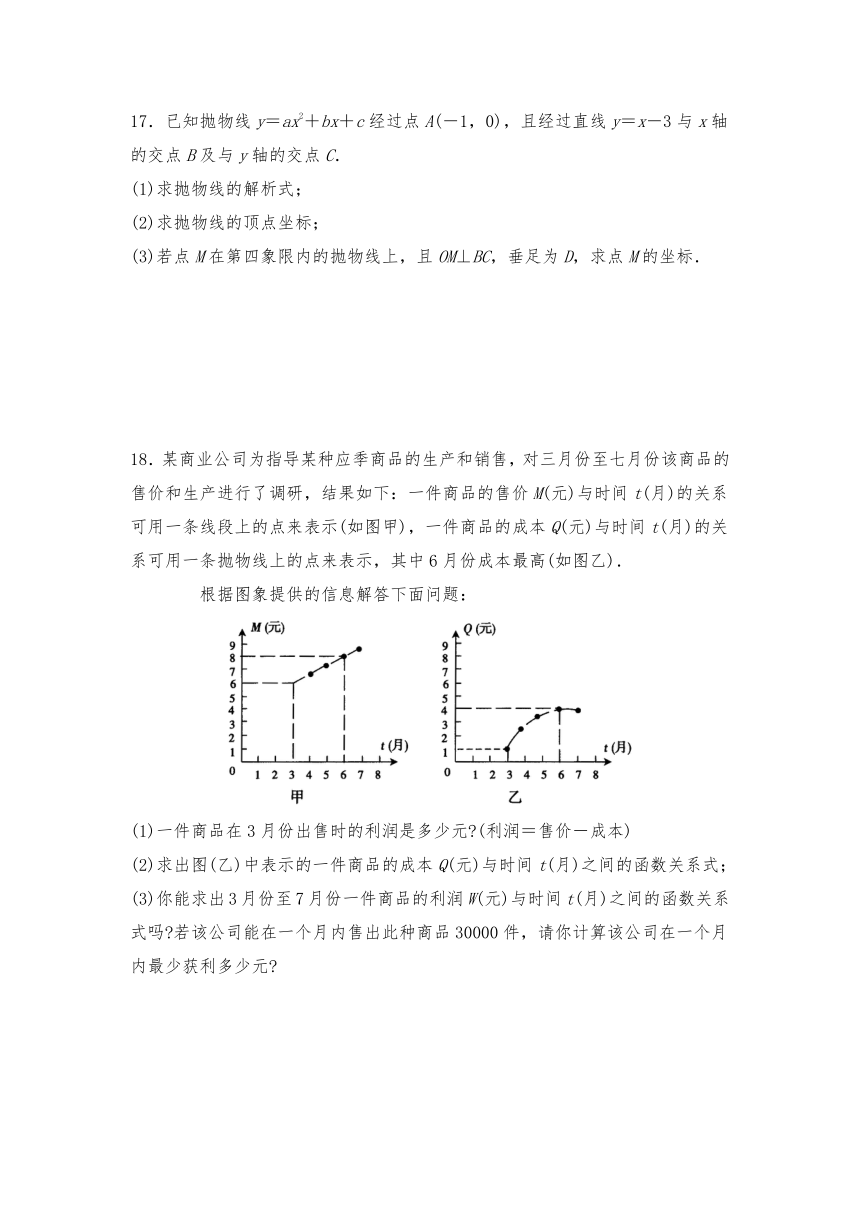
18.某商业公司为指导某种应季商品的生产和销售,对三月份至七月份该商品的售价和生产进行了调研,结果如下:一件商品的售价M(元)与时间t(月)的关系可用一条线段上的点来表示(如图甲),一件商品的成本Q(元)与时间t(月)的关系可用一条抛物线上的点来表示,其中6月份成本最高(如图乙).
根据图象提供的信息解答下面问题:
(1)一件商品在3月份出售时的利润是多少元 (利润=售价-成本)
(2)求出图(乙)中表示的一件商品的成本Q(元)与时间t(月)之间的函数关系式;
(3)你能求出3月份至7月份一件商品的利润W(元)与时间t(月)之间的函数关系式吗 若该公司能在一个月内售出此种商品30000件,请你计算该公司在一个月内最少获利多少元
四、附加题
19.如图甲,Rt△PMN中,∠P=90°,PM=PN,MN=8cm,矩形ABCD的长和宽分别为8cm和2cm,C点和M点重合,BC和MN在一条直线上,令Rt△PMN不动,矩形ABCD沿MN所在直线向右以每秒1cm的速度移动(如图乙),直到C点与N点重合为止.设移动x秒后,矩形ABCD与△PMN重叠部分的面积为ycm2.求y与x之间的函数关系式.
参考答案
1.高,(0,15). 2.y=-x-2. 3.y=x2+4x+3. 4.b=-4.
5.c=5或13. 6.
7.C. 8.D. 9.A. 10.C. 11.C. 12.B. 13.C.
14.顶点坐标,对称轴方程x=3,当y<0时,2<x<4,
图略.
15.当时,
16.(1)由得m=1,n=3.∴y=-x2+4x-3;
(2)S△ACP=6.
17.(1)直线y=x-3与坐标轴的交点坐标分别为B(3,0),C(0,-3),以A、B、C三点的坐标分别代入抛物线y=ax2+bx+c中,得解
得
∴所求抛物线的解析式是y=x2-2x-3.
(2)y=x2-2x-3=(x-1)2-4,
∴抛物线的顶点坐标为(1,-4).
(3)经过原点且与直线y=x-3垂直的直线OM的方程为y=-x,设M(x,-x),
因为M点在抛物线上,∴x2-2x-3=-x.
因点M在第四象限,取
18.解:(1)一件商品在3月份出售时利润为:6-1=5(元).
(2)由图象可知,一件商品的成本Q(元)是时间t(月)的二次函数,由图象可知,
抛物线的顶点为(6,4),
∴可设Q=a(t-6)2+4.
又∵图象过点(3,1),
∴1=a(3-6)2+4,解之
由题知t=3,4,5,6,7.
(3)由图象可知,M(元)是t(月)的一次函数,
∴可设M=kt+b.
∵点(3,6),(6,8)在直线上,
解之
其中t=3,4,5,6,7.
∴当t=5时,元
∴该公司在一月份内最少获利元.
19.解:在Rt△PMN中,∵PM=PN,∠P=90°,
∴∠PMN=∠PNM=45°.延长AD分别交PM、PN于点G、H,过G作GF⊥MN于F,过H作HT⊥MN于T.
∵DC=2cm,∴MF=GF=2cm,TN=HT=2cm.
∵MN=8cm,
∴MT=6cm,因此,矩形ABCD以每秒1cm的速度由开始向右移动到停止,和
Rt△PMN重叠部分的形状,可分为下列三种情况:
(1)当C点由M点运动到F点的过程中(0≤x≤2),如图①所示,设CD与PM交于点E,则重叠部分图形是Rt△MCE,且MC=EC=x,
,即
图①
(2)当C点由F点运动到T点的过程中(2<x≤6),如图②所示,重叠部分图形是直角梯形MCDG.
图②
∵MC=x,MF=2,
∴FC=DG=x-2,且DC=2,
(3)当C点由T点运动到N点的过程中(6<x≤8),如图③所示,设CD与PN交于点Q,则重叠部分图形是五边形MCQHG.
图③
∵MC=x,∴CN=CQ=8-x,且DC=2,
一、填空题
1.抛物线y=-x2+15有最______点,其坐标是______.
2.若抛物线y=x2-2x-2的顶点为A,与y轴的交点为B,则过A,B两点的直线的解析式为____________.
3.若抛物线y=ax2+bx+c(a≠0)的图象与抛物线y=x2-4x+3的图象关于y轴对称,则函数y=ax2+bx+c的解析式为______.
4.若抛物线y=x2+bx+c与y轴交于点A,与x轴正半轴交于B,C两点,且BC=2,S△ABC=3,则b=______.
5.二次函数y=x2-6x+c的图象的顶点与原点的距离为5,则c=______.
6.二次函数的图象在坐标平面内绕顶点旋转180°,再向左平移3个单位,向上平移5个单位后图象对应的二次函数解析式为_______.
二、选择题
7.把二次函数的图象向右平移2个单位后,再向上平移3个单位,所得的函数图象顶点是( )
A.(-5,1) B.(1,-5)
C.(-1,1) D.(-1,3)
8.若点(2,5),(4,5)在抛物线y=ax2+bx+c上,则它的对称轴是( )
A. B.x=1 C.x=2 D.x=3
9.已知函数,当函数值y随x的增大而减小时,x的取值范围是( )
A.x<1 B.x>1 C.x>-2 D.-2<x<4
10.二次函数y=a(x+k)2+k,当k取不同的实数值时,图象顶点所在的直线是( )
A.y=x B.x轴 C.y=-x D.y轴
11.图中有相同对称轴的两条抛物线,下列关系不正确的是( )
A.h=m B.k>n
C.k=n D.h>0,k>0
12.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①abc>0;②a+b+c=2;;④b<1.其中正确的结论是( )
A.①② B.②③
C.②④ D.③④
13.下列命题中,正确的是( )
①若a+b+c=0,则b2-4ac<0;
②若b=2a+3c,则一元二次方程ax2+bx+c=0有两个不相等的实数根;
③若b2-4ac>0,则二次函数y=ax2+bx+c的图象与坐标轴的公共点的个数是2或3;
④若b>a+c,则一元二次方程ax2+bx+c=0,有两个不相等的实数根.
A.②④ B.①③ C.②③ D.③④
三、解答题
14.把二次函数配方成y=a(x-k)2+h的形式,并求出它的图象的顶点坐标、对称轴方程,y<0时x的取值范围,并画出图象.
15.已知二次函数y=ax2+bx+c(a≠0)的图象经过一次函数的图象与x轴、y轴的交点,并也经过(1,1)点.求这个二次函数解析式,并求x为何值时,有最大(最小)值,这个值是什么
16.已知抛物线y=-x2+bx+c与x轴的两个交点分别为A(m,0),B(n,0),且,
(1)求此抛物线的解析式;
(2)设此抛物线与y轴的交点为C,过C作一条平行x轴的直线交抛物线于另一点P,求△ACP的面积.
17.已知抛物线y=ax2+bx+c经过点A(-1,0),且经过直线y=x-3与x轴的交点B及与y轴的交点C.
(1)求抛物线的解析式;
(2)求抛物线的顶点坐标;
(3)若点M在第四象限内的抛物线上,且OM⊥BC,垂足为D,求点M的坐标.
18.某商业公司为指导某种应季商品的生产和销售,对三月份至七月份该商品的售价和生产进行了调研,结果如下:一件商品的售价M(元)与时间t(月)的关系可用一条线段上的点来表示(如图甲),一件商品的成本Q(元)与时间t(月)的关系可用一条抛物线上的点来表示,其中6月份成本最高(如图乙).
根据图象提供的信息解答下面问题:
(1)一件商品在3月份出售时的利润是多少元 (利润=售价-成本)
(2)求出图(乙)中表示的一件商品的成本Q(元)与时间t(月)之间的函数关系式;
(3)你能求出3月份至7月份一件商品的利润W(元)与时间t(月)之间的函数关系式吗 若该公司能在一个月内售出此种商品30000件,请你计算该公司在一个月内最少获利多少元
四、附加题
19.如图甲,Rt△PMN中,∠P=90°,PM=PN,MN=8cm,矩形ABCD的长和宽分别为8cm和2cm,C点和M点重合,BC和MN在一条直线上,令Rt△PMN不动,矩形ABCD沿MN所在直线向右以每秒1cm的速度移动(如图乙),直到C点与N点重合为止.设移动x秒后,矩形ABCD与△PMN重叠部分的面积为ycm2.求y与x之间的函数关系式.
参考答案
1.高,(0,15). 2.y=-x-2. 3.y=x2+4x+3. 4.b=-4.
5.c=5或13. 6.
7.C. 8.D. 9.A. 10.C. 11.C. 12.B. 13.C.
14.顶点坐标,对称轴方程x=3,当y<0时,2<x<4,
图略.
15.当时,
16.(1)由得m=1,n=3.∴y=-x2+4x-3;
(2)S△ACP=6.
17.(1)直线y=x-3与坐标轴的交点坐标分别为B(3,0),C(0,-3),以A、B、C三点的坐标分别代入抛物线y=ax2+bx+c中,得解
得
∴所求抛物线的解析式是y=x2-2x-3.
(2)y=x2-2x-3=(x-1)2-4,
∴抛物线的顶点坐标为(1,-4).
(3)经过原点且与直线y=x-3垂直的直线OM的方程为y=-x,设M(x,-x),
因为M点在抛物线上,∴x2-2x-3=-x.
因点M在第四象限,取
18.解:(1)一件商品在3月份出售时利润为:6-1=5(元).
(2)由图象可知,一件商品的成本Q(元)是时间t(月)的二次函数,由图象可知,
抛物线的顶点为(6,4),
∴可设Q=a(t-6)2+4.
又∵图象过点(3,1),
∴1=a(3-6)2+4,解之
由题知t=3,4,5,6,7.
(3)由图象可知,M(元)是t(月)的一次函数,
∴可设M=kt+b.
∵点(3,6),(6,8)在直线上,
解之
其中t=3,4,5,6,7.
∴当t=5时,元
∴该公司在一月份内最少获利元.
19.解:在Rt△PMN中,∵PM=PN,∠P=90°,
∴∠PMN=∠PNM=45°.延长AD分别交PM、PN于点G、H,过G作GF⊥MN于F,过H作HT⊥MN于T.
∵DC=2cm,∴MF=GF=2cm,TN=HT=2cm.
∵MN=8cm,
∴MT=6cm,因此,矩形ABCD以每秒1cm的速度由开始向右移动到停止,和
Rt△PMN重叠部分的形状,可分为下列三种情况:
(1)当C点由M点运动到F点的过程中(0≤x≤2),如图①所示,设CD与PM交于点E,则重叠部分图形是Rt△MCE,且MC=EC=x,
,即
图①
(2)当C点由F点运动到T点的过程中(2<x≤6),如图②所示,重叠部分图形是直角梯形MCDG.
图②
∵MC=x,MF=2,
∴FC=DG=x-2,且DC=2,
(3)当C点由T点运动到N点的过程中(6<x≤8),如图③所示,设CD与PN交于点Q,则重叠部分图形是五边形MCQHG.
图③
∵MC=x,∴CN=CQ=8-x,且DC=2,
