华师大九年级数学下册26.2《二次函数的图象与性质》习题2- 一课一练试题(word版,含答案)
文档属性
| 名称 | 华师大九年级数学下册26.2《二次函数的图象与性质》习题2- 一课一练试题(word版,含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 512.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 00:00:00 | ||
图片预览




文档简介
26.2《二次函数的图象与性质》习题2
一、选择题
1.函数y=x2-4的图象与y轴的交点坐标是( )
A.(2,0) B.(-2,0) C.(0,4) D.(0,-4)
2.(2008年上海市)在平面直角坐标系中,抛物线与轴的交点的个数是( )
A.3 B.2 C.1 D.0
3.抛物线经过第一、三、四象限,则抛物线的顶点必在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.二次函数的图象与轴有交点,则的取值范围是( )
A. B. C. D.
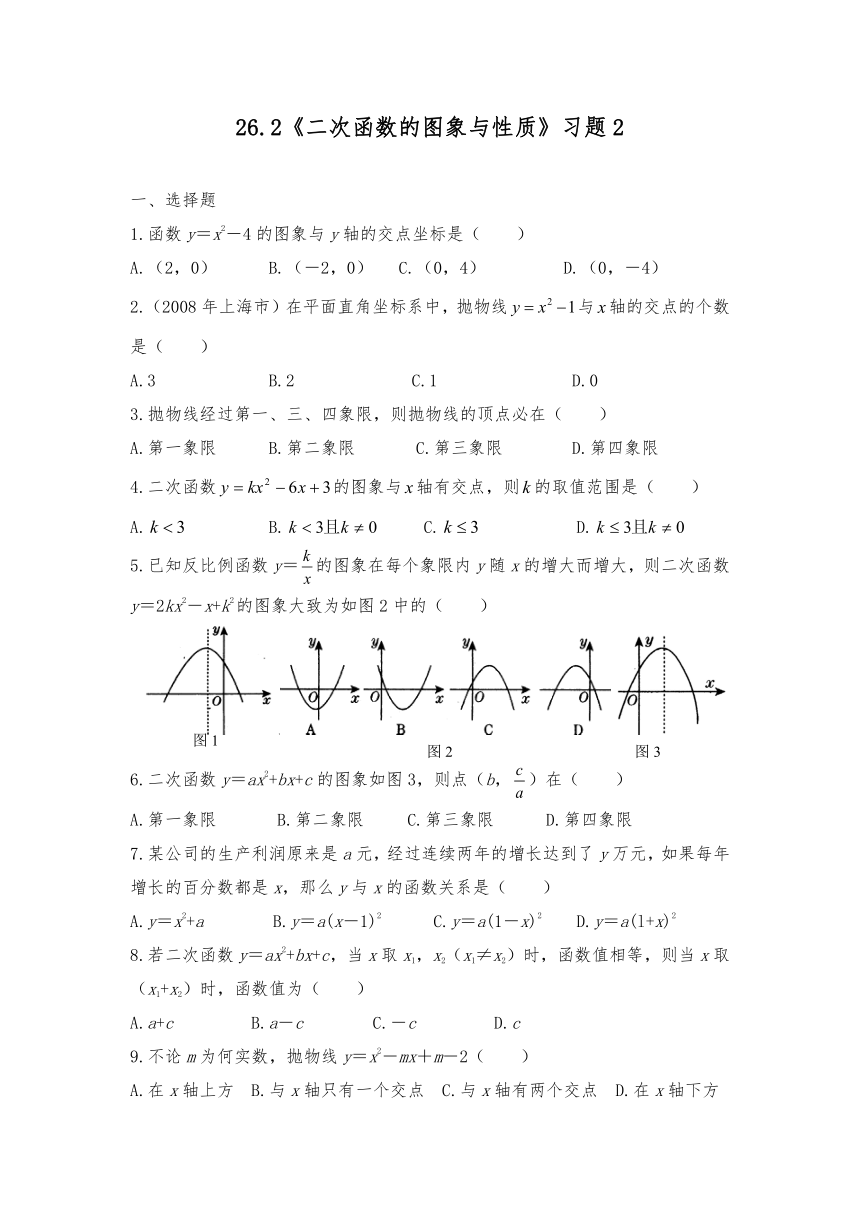
5.已知反比例函数y=的图象在每个象限内y随x的增大而增大,则二次函数y=2kx2-x+k2的图象大致为如图2中的( )
6.二次函数y=ax2+bx+c的图象如图3,则点(b,)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.某公司的生产利润原来是a元,经过连续两年的增长达到了y万元,如果每年增长的百分数都是x,那么y与x的函数关系是( )
A.y=x2+a B.y=a(x-1)2 C.y=a(1-x)2 D.y=a(l+x)2
8.若二次函数y=ax2+bx+c,当x取x1,x2(x1≠x2)时,函数值相等,则当x取(x1+x2)时,函数值为( )
A.a+c B.a-c C.-c D.c
9.不论m为何实数,抛物线y=x2-mx+m-2( )
A.在x轴上方 B.与x轴只有一个交点 C.与x轴有两个交点 D.在x轴下方
10.若二次函数y=x2-x与y=-x2+k的图象的顶点重合,则下列结论不正确的是( )
A.这两个函数图象有相同的对称轴 B.这两个函数图象的开口方向相反
C.方程-x2+k=0没有实数根 D.二次函数y=-x2+k的最大值为
二、填空题
11.顶点为(-2,-5)且过点(1,-14)的抛物线的解析式为 .
12.若点A(2,m)在抛物线y=x2上,则点A关于y轴对称点的坐标是 .
13.二次函数y=2x2+bx+c的顶点坐标是(1,-2).则b= ,c= .
14.已知二次函数y=ax2+bx+c (a≠0)与一次函数y=kx+m(k≠0)的图象相交于点A(-2,4),B(8,2),如图4所示,能使y1>y2成立的x取值范围是 .
15.小王利用计算机设计了一个计算程序,输入和输出的数据如下表:
输入 … 1 2 3 4 5 …
输出 … 2 5 10 17 26 …
若输入的数据是x时,输出的数据是y,y是x的二次函数,则y与x 的函数表达式为 .
16.平移抛物线y=x2+2x-8,使它经过原点,写出平移后抛物线的一个解析式 .
17.抛物线y=ax2+bx+c中,已知a∶b∶c=l∶2∶3,最小值为6,则此抛物线的解析式为 .
18.把一根长100cm的铁丝分为两部分,每一部分均弯曲成一个正方形,它们的面积和最小是 .
三、解答题
19.利用二次函数的图象求下列方程的近似根:
(1)x2+x-12=0;(2)2x2-x-3=0.
20.已知抛物线与x轴交于点(1,0)和(2,0)且过点 (3,4).求抛物线的解析式.
21.已知二次函数y=x2-6x+8.求:
(1)抛物线与x轴和y轴相交的交点坐标;
(2)抛物线的顶点坐标;
(3)画出此抛物线图象,利用图象回答下列问题:
①方程x2-6x+8=0的解是什么?
②x取什么值时,函数值大于0?
③x取什么值时,函数值小于0?
22.当 x=4时,函数y=ax2+bx+c的最小值为-8,抛物线过点(6,0).求:
(1)顶点坐标和对称轴;
(2)函数的表达式;
(3)x取什么值时,y随x的增大而增大;x取什么值时,y随x增大而减小.
23.已知抛物线y=x2-2x-8.
(1)求证:该抛物线与x轴一定有两个交点;
(2)若该抛物线与x轴的两个交点分别为A、B,且它的顶点为P,求△ABP的面积.
24.如图5,宜昌西陵长江大桥属于抛物线形悬索桥,桥面(视为水平的)与主悬钢索之间用垂直钢拉索连接.桥两端主塔塔顶的海拔高度均是187.5米,桥的单孔跨度(即两主塔之间的距离)900米,这里水面的海拔高度是74米.若过主塔塔顶的主悬钢索(视为抛物线)最低点离桥面(视为直线)的高度为0.5米,桥面离水面的高度为19米.请你计算距离桥两端主塔100米处垂直钢拉索的长(结果精确到0.1米).
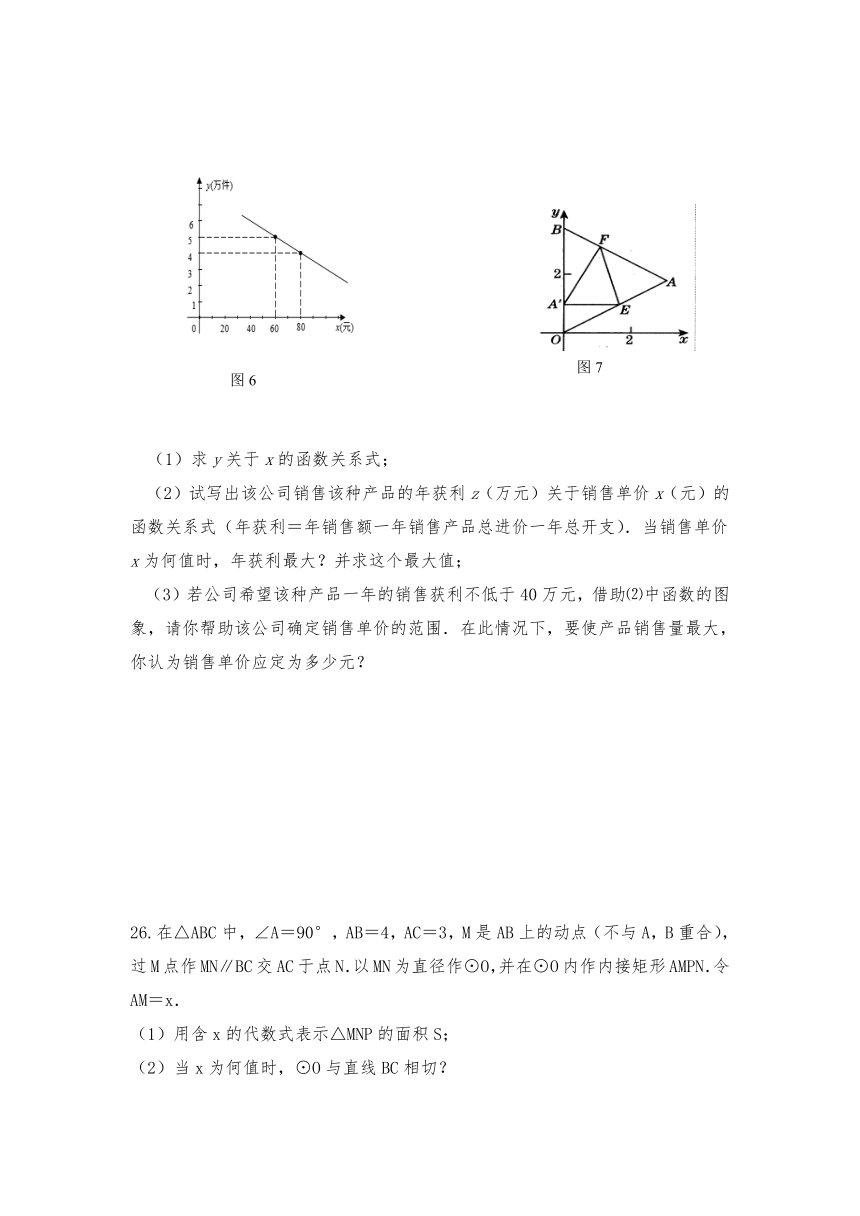
某通讯器材公司销售一种市场需求较大的新型通讯产品.已知每件产品的进价为40元,每年销售该种产品的总开支(不含进价)总计120万元.在销售过程中发现,年销售量y(万件)与销售单价x(元)之问存在着如图6所示的一次函数关系.
(1)求y关于x的函数关系式;
(2)试写出该公司销售该种产品的年获利z(万元)关于销售单价x(元)的函数关系式(年获利=年销售额一年销售产品总进价一年总开支).当销售单价x为何值时,年获利最大?并求这个最大值;
(3)若公司希望该种产品一年的销售获利不低于40万元,借助⑵中函数的图象,请你帮助该公司确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?
26.在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.
(1)用含x的代数式表示△MNP的面积S;
(2)当x为何值时,⊙O与直线BC相切?
(3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?
参考答案
一、1.D; 2.B; 3.A; 4.D; 5.D; 6.D; 7.D; 8.D.9.C; 10.C.
二、11.y=-x2-4x-9;
12. (-2,4);
13.-4、0;
14.x<-2或x>8;
15.y=x2+1;
16.答案不惟一,如,y=x2+2x;
17.y=3x2+6x+9;
18.312.5cm2.
三、19.函数y=ax2+bx+c与x轴的两个交点的横坐标就是方程ax2+bx+c=的解;
20.y=2x2-6x+4;
21.(1)由题意,得x2-6x+8=0.则(x-2) (x-4)=0,x1=2,x2=4.所以与x轴交点为(2,0)和(4,0),当x=0时,y=8.所以抛物线与y轴交点为(0,8),(2)抛物线的顶点坐标为(3,-1),(3)如图1所示.①由图象知,x2-6x+8=0的解为x1=2,x2=4.②当x<2或x>4时,函数值大于0;③当2<x<4时,函数值小于0;
22.(1)(4,-8),x=4,(2)y=2x2-16x+24,(3)x>4时,y随x的增大而增大,x<4时,y随x的增大而减小;
23.(1)证明:因为对于方程x2-2x-8=0,有x1=2,x2=4,即所以方程x2-2x-8=0有两个实根,抛物线y=x2-2x-8与x轴一定有两个交点;(2)解:因为方程x2-2x-8=0有两个根为x1=2,x2=4,所以AB=| x1-x2|=6.又抛物线顶点P的纵坐标yP==-9,所以SΔABP=×AB×|yP|=27;
24.如图2,以桥面上位于主悬钢索最低点的正下方一点坐标原点,以桥面所在的直线为x轴建立平面直角坐标系,则A(0,0.5),B(-450, 94.5),C(450,94.5).由题意,设抛物线为:y=ax2+0.5. 将C(450,94.5)代入求得:或.所以.当x=350时,y=57.4;当x=400时,y=74.8.所以,离桥两端主塔100米处竖直钢拉索的长都约为57.4米,离桥两端主塔50米处竖直钢拉索的长都约为74.8米.
25.(1)由图象中提供的信息可设y=kx+b,此时的图象过点(60,5),(80,4),于是,有解得所以y关于x的函数关系式是y=-x+8.
(2)z=yx-40y-120=(-x+8)(x-40)=-x2+10x-440,所以当x=100元时,最大年获得为60万元.
(3)依题意可画出(2)中的图象,如图3,令z=40,得40=-x2+10x-440,整理,得x2-200x+9600=0,解得x1=80,x2=120. 由图象可知,要使年获利不低于40万元,销售单价应在80元到120元之间.又因为销售单价越低,销售量越大,所以要使销售量最大,又要使年获利不低于40万元,销售单价应定为80元.
26.解:(1)∵MN∥BC,∴∠AMN=∠B,∠ANM=∠C.
∴ △AMN ∽ △ABC.
∴ ,即.
∴ AN=x.
∴ =.(0<<4)
(2)
如图2,设直线BC与⊙O相切于点D,连结AO,OD,则AO =OD =MN.
在Rt△ABC中,BC ==5.
由(1)知 △AMN ∽ △ABC.
∴ ,即.
∴ ,
∴ .
过M点作MQ⊥BC 于Q,则.
在Rt△BMQ与Rt△BCA中,∠B是公共角,
∴ △BMQ∽△BCA.
∴ .
∴ ,.
∴ x=.
∴ 当x=时,⊙O与直线BC相切.
(3)随点M的运动,当P点落在直线BC上时,连结AP,则O点为AP的中点.
∵ MN∥BC,∴ ∠AMN=∠B,∠AOM=∠APC.
∴ △AMO ∽ △ABP.
∴ . AM=MB=2.
故以下分两种情况讨论:
① 当0<≤2时,.
∴ 当=2时,
② 当2<<4时,设PM,PN分别交BC于E,F.
∵ 四边形AMPN是矩形,
∴ PN∥AM,PN=AM=x.
又∵ MN∥BC,
∴ 四边形MBFN是平行四边形.
∴ FN=BM=4-x.
∴ .
又△PEF ∽ △ACB.
∴ .
∴ .
=.
当2<<4时,.
∴ 当时,满足2<<4,.
综上所述,当时,值最大,最大值是2.
一、选择题
1.函数y=x2-4的图象与y轴的交点坐标是( )
A.(2,0) B.(-2,0) C.(0,4) D.(0,-4)
2.(2008年上海市)在平面直角坐标系中,抛物线与轴的交点的个数是( )
A.3 B.2 C.1 D.0
3.抛物线经过第一、三、四象限,则抛物线的顶点必在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.二次函数的图象与轴有交点,则的取值范围是( )
A. B. C. D.
5.已知反比例函数y=的图象在每个象限内y随x的增大而增大,则二次函数y=2kx2-x+k2的图象大致为如图2中的( )
6.二次函数y=ax2+bx+c的图象如图3,则点(b,)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.某公司的生产利润原来是a元,经过连续两年的增长达到了y万元,如果每年增长的百分数都是x,那么y与x的函数关系是( )
A.y=x2+a B.y=a(x-1)2 C.y=a(1-x)2 D.y=a(l+x)2
8.若二次函数y=ax2+bx+c,当x取x1,x2(x1≠x2)时,函数值相等,则当x取(x1+x2)时,函数值为( )
A.a+c B.a-c C.-c D.c
9.不论m为何实数,抛物线y=x2-mx+m-2( )
A.在x轴上方 B.与x轴只有一个交点 C.与x轴有两个交点 D.在x轴下方
10.若二次函数y=x2-x与y=-x2+k的图象的顶点重合,则下列结论不正确的是( )
A.这两个函数图象有相同的对称轴 B.这两个函数图象的开口方向相反
C.方程-x2+k=0没有实数根 D.二次函数y=-x2+k的最大值为
二、填空题
11.顶点为(-2,-5)且过点(1,-14)的抛物线的解析式为 .
12.若点A(2,m)在抛物线y=x2上,则点A关于y轴对称点的坐标是 .
13.二次函数y=2x2+bx+c的顶点坐标是(1,-2).则b= ,c= .
14.已知二次函数y=ax2+bx+c (a≠0)与一次函数y=kx+m(k≠0)的图象相交于点A(-2,4),B(8,2),如图4所示,能使y1>y2成立的x取值范围是 .
15.小王利用计算机设计了一个计算程序,输入和输出的数据如下表:
输入 … 1 2 3 4 5 …
输出 … 2 5 10 17 26 …
若输入的数据是x时,输出的数据是y,y是x的二次函数,则y与x 的函数表达式为 .
16.平移抛物线y=x2+2x-8,使它经过原点,写出平移后抛物线的一个解析式 .
17.抛物线y=ax2+bx+c中,已知a∶b∶c=l∶2∶3,最小值为6,则此抛物线的解析式为 .
18.把一根长100cm的铁丝分为两部分,每一部分均弯曲成一个正方形,它们的面积和最小是 .
三、解答题
19.利用二次函数的图象求下列方程的近似根:
(1)x2+x-12=0;(2)2x2-x-3=0.
20.已知抛物线与x轴交于点(1,0)和(2,0)且过点 (3,4).求抛物线的解析式.
21.已知二次函数y=x2-6x+8.求:
(1)抛物线与x轴和y轴相交的交点坐标;
(2)抛物线的顶点坐标;
(3)画出此抛物线图象,利用图象回答下列问题:
①方程x2-6x+8=0的解是什么?
②x取什么值时,函数值大于0?
③x取什么值时,函数值小于0?
22.当 x=4时,函数y=ax2+bx+c的最小值为-8,抛物线过点(6,0).求:
(1)顶点坐标和对称轴;
(2)函数的表达式;
(3)x取什么值时,y随x的增大而增大;x取什么值时,y随x增大而减小.
23.已知抛物线y=x2-2x-8.
(1)求证:该抛物线与x轴一定有两个交点;
(2)若该抛物线与x轴的两个交点分别为A、B,且它的顶点为P,求△ABP的面积.
24.如图5,宜昌西陵长江大桥属于抛物线形悬索桥,桥面(视为水平的)与主悬钢索之间用垂直钢拉索连接.桥两端主塔塔顶的海拔高度均是187.5米,桥的单孔跨度(即两主塔之间的距离)900米,这里水面的海拔高度是74米.若过主塔塔顶的主悬钢索(视为抛物线)最低点离桥面(视为直线)的高度为0.5米,桥面离水面的高度为19米.请你计算距离桥两端主塔100米处垂直钢拉索的长(结果精确到0.1米).
某通讯器材公司销售一种市场需求较大的新型通讯产品.已知每件产品的进价为40元,每年销售该种产品的总开支(不含进价)总计120万元.在销售过程中发现,年销售量y(万件)与销售单价x(元)之问存在着如图6所示的一次函数关系.
(1)求y关于x的函数关系式;
(2)试写出该公司销售该种产品的年获利z(万元)关于销售单价x(元)的函数关系式(年获利=年销售额一年销售产品总进价一年总开支).当销售单价x为何值时,年获利最大?并求这个最大值;
(3)若公司希望该种产品一年的销售获利不低于40万元,借助⑵中函数的图象,请你帮助该公司确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?
26.在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.
(1)用含x的代数式表示△MNP的面积S;
(2)当x为何值时,⊙O与直线BC相切?
(3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?
参考答案
一、1.D; 2.B; 3.A; 4.D; 5.D; 6.D; 7.D; 8.D.9.C; 10.C.
二、11.y=-x2-4x-9;
12. (-2,4);
13.-4、0;
14.x<-2或x>8;
15.y=x2+1;
16.答案不惟一,如,y=x2+2x;
17.y=3x2+6x+9;
18.312.5cm2.
三、19.函数y=ax2+bx+c与x轴的两个交点的横坐标就是方程ax2+bx+c=的解;
20.y=2x2-6x+4;
21.(1)由题意,得x2-6x+8=0.则(x-2) (x-4)=0,x1=2,x2=4.所以与x轴交点为(2,0)和(4,0),当x=0时,y=8.所以抛物线与y轴交点为(0,8),(2)抛物线的顶点坐标为(3,-1),(3)如图1所示.①由图象知,x2-6x+8=0的解为x1=2,x2=4.②当x<2或x>4时,函数值大于0;③当2<x<4时,函数值小于0;
22.(1)(4,-8),x=4,(2)y=2x2-16x+24,(3)x>4时,y随x的增大而增大,x<4时,y随x的增大而减小;
23.(1)证明:因为对于方程x2-2x-8=0,有x1=2,x2=4,即所以方程x2-2x-8=0有两个实根,抛物线y=x2-2x-8与x轴一定有两个交点;(2)解:因为方程x2-2x-8=0有两个根为x1=2,x2=4,所以AB=| x1-x2|=6.又抛物线顶点P的纵坐标yP==-9,所以SΔABP=×AB×|yP|=27;
24.如图2,以桥面上位于主悬钢索最低点的正下方一点坐标原点,以桥面所在的直线为x轴建立平面直角坐标系,则A(0,0.5),B(-450, 94.5),C(450,94.5).由题意,设抛物线为:y=ax2+0.5. 将C(450,94.5)代入求得:或.所以.当x=350时,y=57.4;当x=400时,y=74.8.所以,离桥两端主塔100米处竖直钢拉索的长都约为57.4米,离桥两端主塔50米处竖直钢拉索的长都约为74.8米.
25.(1)由图象中提供的信息可设y=kx+b,此时的图象过点(60,5),(80,4),于是,有解得所以y关于x的函数关系式是y=-x+8.
(2)z=yx-40y-120=(-x+8)(x-40)=-x2+10x-440,所以当x=100元时,最大年获得为60万元.
(3)依题意可画出(2)中的图象,如图3,令z=40,得40=-x2+10x-440,整理,得x2-200x+9600=0,解得x1=80,x2=120. 由图象可知,要使年获利不低于40万元,销售单价应在80元到120元之间.又因为销售单价越低,销售量越大,所以要使销售量最大,又要使年获利不低于40万元,销售单价应定为80元.
26.解:(1)∵MN∥BC,∴∠AMN=∠B,∠ANM=∠C.
∴ △AMN ∽ △ABC.
∴ ,即.
∴ AN=x.
∴ =.(0<<4)
(2)
如图2,设直线BC与⊙O相切于点D,连结AO,OD,则AO =OD =MN.
在Rt△ABC中,BC ==5.
由(1)知 △AMN ∽ △ABC.
∴ ,即.
∴ ,
∴ .
过M点作MQ⊥BC 于Q,则.
在Rt△BMQ与Rt△BCA中,∠B是公共角,
∴ △BMQ∽△BCA.
∴ .
∴ ,.
∴ x=.
∴ 当x=时,⊙O与直线BC相切.
(3)随点M的运动,当P点落在直线BC上时,连结AP,则O点为AP的中点.
∵ MN∥BC,∴ ∠AMN=∠B,∠AOM=∠APC.
∴ △AMO ∽ △ABP.
∴ . AM=MB=2.
故以下分两种情况讨论:
① 当0<≤2时,.
∴ 当=2时,
② 当2<<4时,设PM,PN分别交BC于E,F.
∵ 四边形AMPN是矩形,
∴ PN∥AM,PN=AM=x.
又∵ MN∥BC,
∴ 四边形MBFN是平行四边形.
∴ FN=BM=4-x.
∴ .
又△PEF ∽ △ACB.
∴ .
∴ .
=.
当2<<4时,.
∴ 当时,满足2<<4,.
综上所述,当时,值最大,最大值是2.
