2021-2022学年人教版九年级数学下册第二十九章 投影与视图 定向测评试卷(word版 含解析)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册第二十九章 投影与视图 定向测评试卷(word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 437.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 13:46:20 | ||
图片预览

文档简介
人教版九年级数学下册第二十九章-投影与视图定向测评
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、下面图形是某几何体的三视图(其中主视图也称正视图,左视图也称侧视图),则这个几何体是( )
A.四棱柱 B.四棱锥 C.圆柱 D.圆锥
2、如图是由几个大小相同的小正方体搭成的几何体,若去掉1号小正方体,则下列说法正确的是( )
A.左视图和俯视图不变 B.主视图和左视图不变
C.主视图和俯视图不变 D.都不变
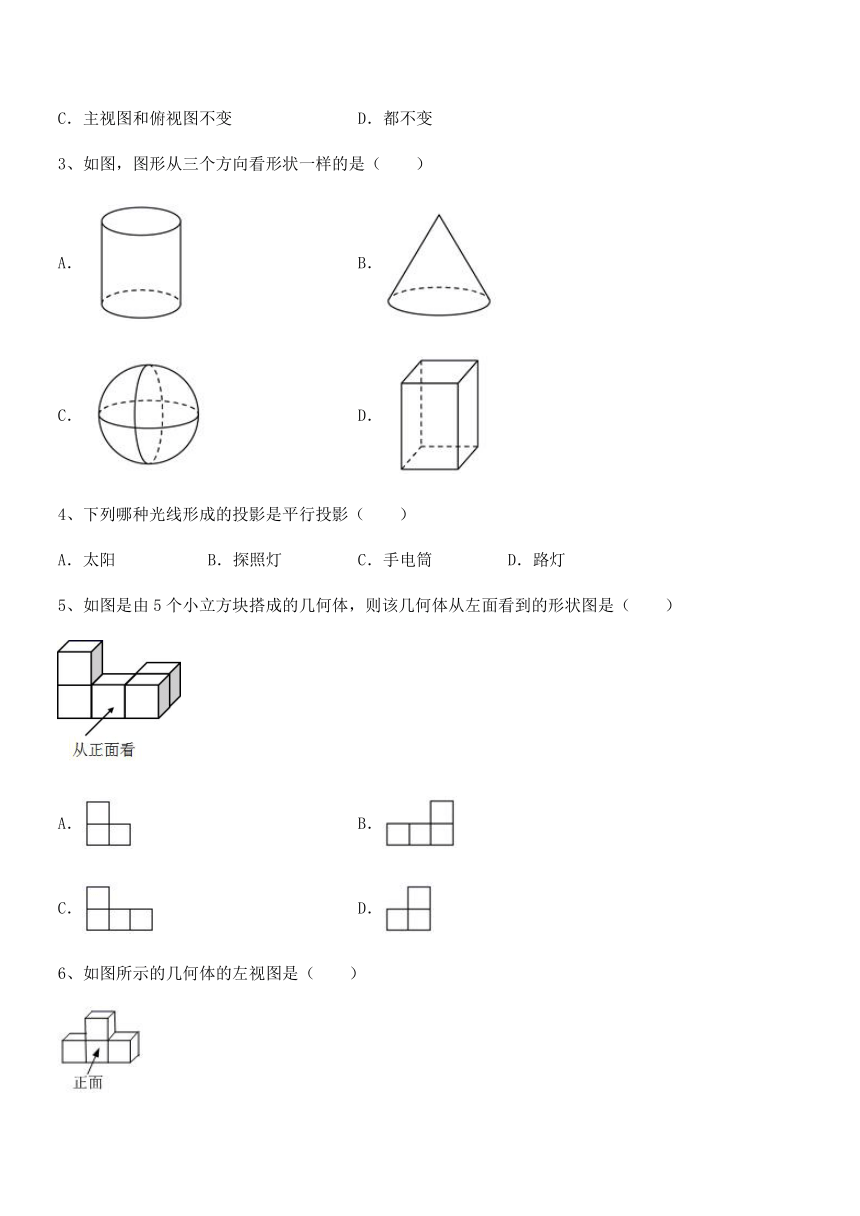
3、如图,图形从三个方向看形状一样的是( )
A. B.
C. D.
4、下列哪种光线形成的投影是平行投影( )
A.太阳 B.探照灯 C.手电筒 D.路灯
5、如图是由5个小立方块搭成的几何体,则该几何体从左面看到的形状图是( )
A. B.
C. D.
6、如图所示的几何体的左视图是( )
A. B. C. D.
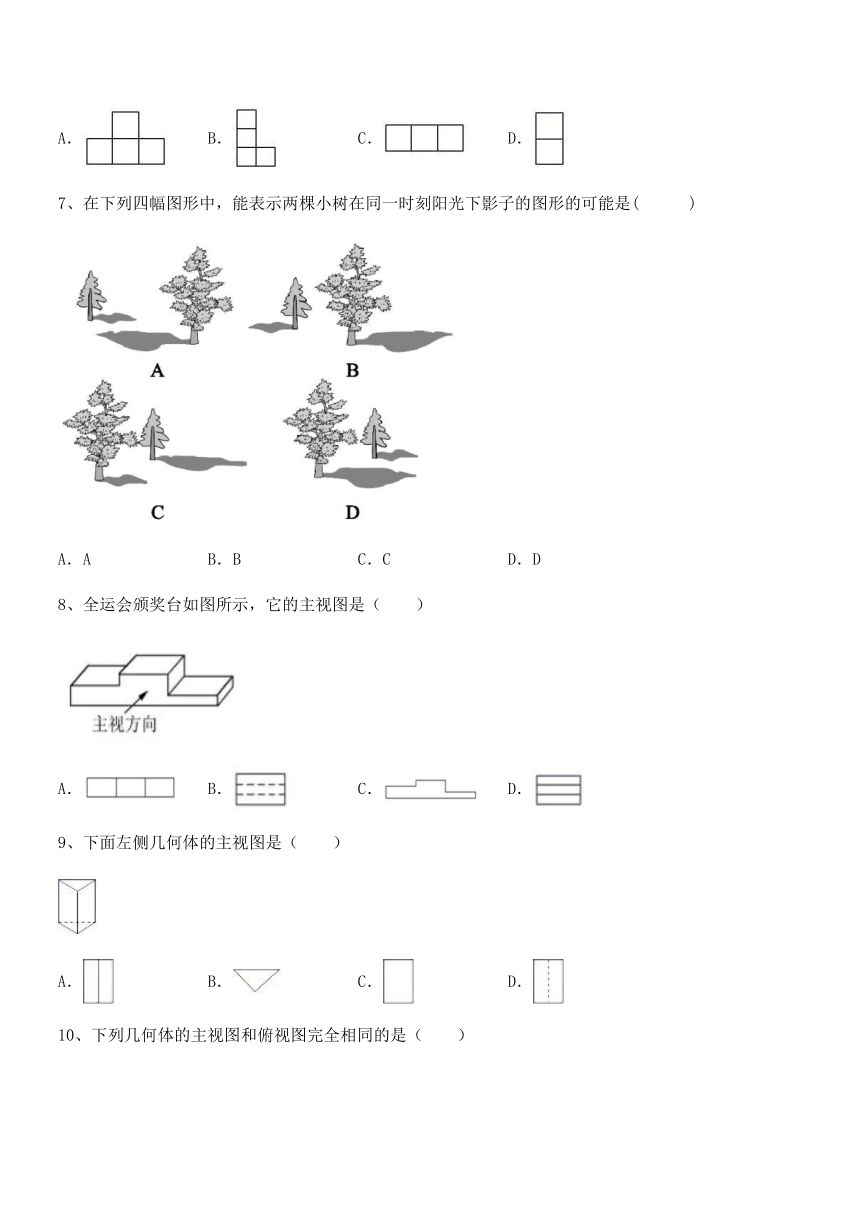
7、在下列四幅图形中,能表示两棵小树在同一时刻阳光下影子的图形的可能是( )
A.A B.B C.C D.D
8、全运会颁奖台如图所示,它的主视图是( )
A. B. C. D.
9、下面左侧几何体的主视图是( )
A. B. C. D.
10、下列几何体的主视图和俯视图完全相同的是( )
A. B. C. D.
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
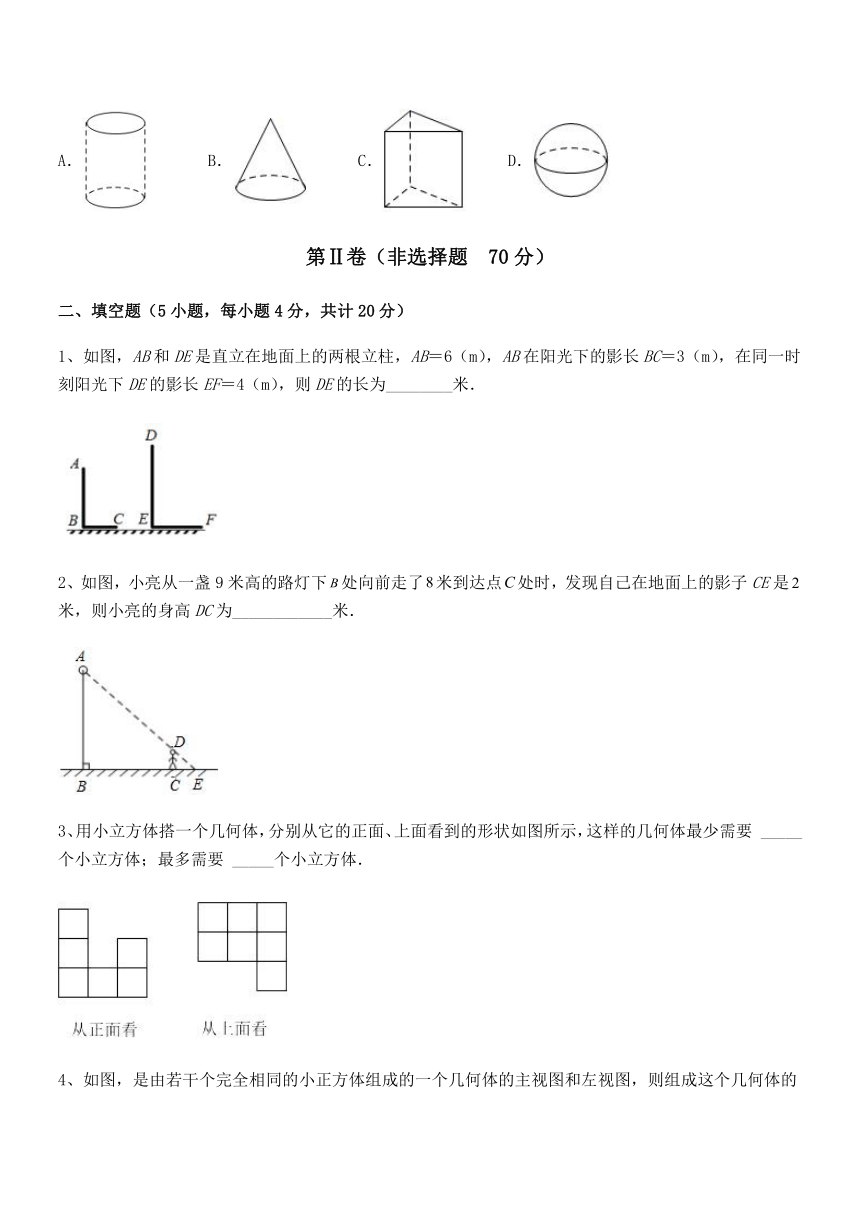
1、如图,AB和DE是直立在地面上的两根立柱,AB=6(m),AB在阳光下的影长BC=3(m),在同一时刻阳光下DE的影长EF=4(m),则DE的长为________米.
2、如图,小亮从一盏9米高的路灯下处向前走了米到达点处时,发现自己在地面上的影子CE是米,则小亮的身高DC为____________米.
3、用小立方体搭一个几何体,分别从它的正面、上面看到的形状如图所示,这样的几何体最少需要 _____个小立方体;最多需要 _____个小立方体.
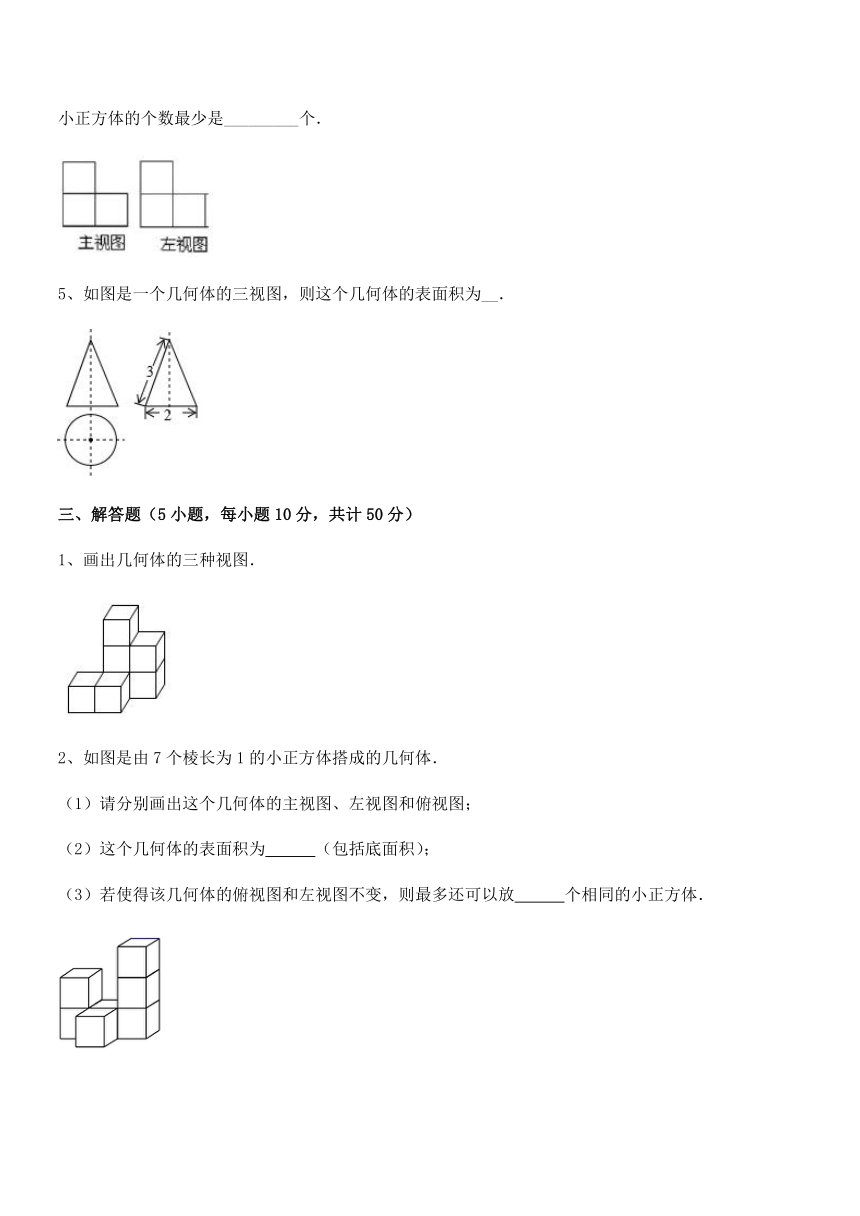
4、如图,是由若干个完全相同的小正方体组成的一个几何体的主视图和左视图,则组成这个几何体的小正方体的个数最少是_________个.
5、如图是一个几何体的三视图,则这个几何体的表面积为__.
三、解答题(5小题,每小题10分,共计50分)
1、画出几何体的三种视图.
2、如图是由7个棱长为1的小正方体搭成的几何体.
(1)请分别画出这个几何体的主视图、左视图和俯视图;
(2)这个几何体的表面积为 (包括底面积);
(3)若使得该几何体的俯视图和左视图不变,则最多还可以放 个相同的小正方体.
3、用小正方体搭成一个几何体,使得从正面看、从上面看该几何体得到的图形如图所示.问:
(1)这样的几何体只有一种吗?它最多需要多少个小正方体?
(2)它最少需要多少个小正方体?请分别画出这两种情况下从左面看该几何体得到的图形.
4、如图,是由小立方块塔成的几何体,请画出这个几何体从正面、左面、上面三个方面看到的形状图:
5、一个几何体由大小相同的小立方块搭成,箭头所指的为正面,请画出从正面、左面、上面看到的几何体的形状图.
---------参考答案-----------
一、单选题
1、C
【分析】
根据三视图即可完成.
【详解】
此几何体为一个圆柱
故选:C.
【点睛】
本题考查由三视图还原几何体,既要考虑各视图的形状,还要把各视图的情况综合考虑才能得到几何体的形状.
2、A
【分析】
根据从正面看得到的图形是主视图,从左边看得到的图形是左视图,从上边看得到的图形是俯视图,再从看到的小正方形的个数与排列方式两个方面逐一分析可得答案.
【详解】
解:若去掉1号小正方体, 主视图一定变化,主视图中最右边的一列由两个小正方形变为一个,
从上面看过去,看到的小正方形的个数与排列方式不变,所以俯视图不变,
从左边看过去,看到的小正方形的个数与排列方式不变; 所以左视图不变,
所以A符合题意,B,C,D不符合题意;
故选:A.
【点睛】
本题考查的是由小正方体堆砌而成的图形的三视图,掌握“三视图的含义”是解本题的关键.
3、C
【分析】
根据从上面看得到的图形是俯视图,从正面看得到的图形是主视图,从左边看得到的图形是左视图,可得答案.
【详解】
解:A.从上面看是一个圆,从正面和从左边看是一个矩形,故本选项不合题意;
B.从上面看是一个有圆心的圆,从正面和从左边看是一个等腰三角形,故本选项不合题意;
C.从三个方向看形状一样,都是圆形,故本选项符合题意;
D.从上面看是一个正方形,从正面和从左边看是一个长方形形,故本选项不合题意.
故选:C.
【点睛】
本题考查了简单几何体的三视图,从上面看到的图形是俯视图,从正面看到的图形是主视图,从左面看到的图形是左视图.
4、A
【分析】
中心投影是指把光由一点向外散射形成的投影,平行投影是在一束平行光线照射下形成的投影,根据定义逐一分析即可得到答案.
【详解】
解:太阳光线形成的投影是平行投影,
探照灯,手电筒,路灯形成的投影是中心投影,
故选A
【点睛】
本题考查的是平行投影与中心投影的含义及应用,根据定义熟练判断中心投影与平行投影是解题的关键.
5、D
【分析】
左视图:从左边看立体图形,看到的平面图形是左视图,根据左视图的定义可得答案.
【详解】
解:该几何体从左面看到的形状图有2列,
第1列看到1个正方形,第2列看到2个正方形,
所以左视图是D,
故选D
【点睛】
本题考查的是三视图,值得注意的是能看到的立体图形中的线条都要画成实线,看不到的画成虚线,掌握“左视图的含义”是解题的关键.
6、D
【分析】
根据左视图的定义即可得.
【详解】
解:左视图是指从左面观察几何体所得到的视图,
这个几何体的左视图是,
故选:D.
【点睛】
本题考查了左视图,熟记定义是解题关键.
7、D
【分析】
由太阳光是平行光线,可知同一时刻下,影子的朝向一致,由此进行求解即可.
【详解】
解:太阳光是平行光线,因此同一时刻下,影子的朝向是一致的.
故选:D.
【点睛】
考查主要考查了的影子问题,解题的关键在于能够知道太阳光是平行光线.
8、C
【分析】
主视图是从前面先后看得到的图形,根据主视图对各选项一一分析即可.
【详解】
解:主视图是从前面先后看得到的图形,是C.
故选C.
【点睛】
本题考查主视图,掌握三视图的特征是解题关键.
9、A
【分析】
找出从几何体的正面看所得到的图形即可.
【详解】
解:从几何体的正面看,是一行两个并列的矩形.
故选:A.
【点睛】
本题主要考查了几何体的三视图,准确分析判断是解题的关键.
10、D
【分析】
根据主视图和俯视图是分别从物体正面和上面看到的图形,逐项分析即可.
【详解】
解:A、圆柱主视图是矩形,俯视图是圆,故A选项不合题意;
B、圆锥的主视图是等腰三角形,俯视图是圆以及中心有一个点,故B选项不合题意;
C、三棱柱主视图是一行两个矩形且公共边是虚线,俯视图是三角形,故C选项不合题意;
D、圆的主视图和俯视图都为圆,故D选项符合题意;
故选D.
【点睛】
本题考查简单几何体的三视图,解决问题的关键是掌握主视图是从物体的正面看到的视图,俯视图是从物体的上面看得到的视图.
二、填空题
1、8
【解析】
【分析】
连接,,根据平行投影的性质得,根据平行的性质可知,利用相似三角形对应边成比例即可求出的长.
【详解】
解:如图,连接AC ,DF,根据平行投影的性质得DF∥AC,
,
,
,
,
,
.
故答案为:8.
【点睛】
本题主要考查相似三角形的判定和性质,掌握相似三角形的判定定理以及性质是解题的关键.
2、1.8
【解析】
【分析】
同一时刻下物体高度的比等于影长的比,构造相似三角形计算即可.
【详解】
如图,由题意知米,米,米,且,
∴米,
∵,
∴
又∵
∴,
∴,即,
解得(米),即小亮的身高为1.8米;
故答案为:1.8.
【点睛】
本题考查平行投影的相关知识点,能够根据题意构造相似是解题关键点.
3、 10 14
【解析】
【分析】
从上面看中可以看出最底层小正方体的个数及形状,从前面看可以看出每一层小正方体的层数和个数,从而算出总的个数.
【详解】
解:∵从上面看有7个正方形,
∴最底层有7个正方体,
从前面看可得第2层最少有2个正方体;最多有5个正方体,
第3层最少有1个正方体;最多有2个正方体,
∴该组合几何体最少有7+2+1=10个正方体,最多有7+5+2=14个正方体.
故答案为:10,14.
【点睛】
此题主要考查了不同方向看几何体,关键是掌握口诀“上面看打地基,前面看疯狂盖,左面看拆违章”就很容易得到答案.
4、3
【解析】
【分析】
画出模拟俯视图,根据主对列,左对行进行标数,相同取同,不同取0即可得出答案.
【详解】
已知主视图和左视图求堆积几何体最少的情况:画模拟俯视图,主对列,左对行进行标数,相同取同,不同取0.具体如下图:
故答案为:3.
【点睛】
考查学生对三视图的掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,主视图疯狂盖,左视图拆违章”就更容易得到答案.
5、4π
【解析】
【分析】
先判定这个几何体是圆锥,再根据圆锥的特点求出其表面积.
【详解】
解:根据三视图可得这个几何体是圆锥,
底面积=π×12=π,
侧面积为==3π,
则这个几何体的表面积=π+3π=4π;
故答案为:4π.
【点睛】
此题主要考查圆锥的表面积,解题的关键是根据三视图的得到几何体是圆锥.
三、解答题
1、见详解
【分析】
从正面看从左往右3列正方形的个数依次为1,3,2;从左面看从左往右3列正方形的个数依次为3,1;从上面看从左往右3列正方形的个数依次为1,2,1.依此画出图形.
【详解】
解:如图所示:
【点睛】
本题考查了三视图的画法;得到从各个方向看得到的每列正方形的个数是解决本题的关键.
2、(1)见解析;(2)30;(3)3
【分析】
(1)根据三视图的画法画出相应的图形即可;
(2)三视图面积的2倍加被挡住的面积即可;
(3)根据俯视图和左视图的特点即可求解.
【详解】
(1)这个几何体的主视图、左视图和俯视图如下:
(2)(6+4+4)×2+2=30,
故答案为:30;
(3)保持这个几何体的俯视图和左视图不变,可往第一列和第二列分别添加1个、2个小正方体,
故答案为:3.
【点睛】
此题主要考查了三视图,正确掌握不同视图的观察角度是解题关键.
3、(1)不止一种,最多14个;(2)最小10个,画图见解析
【分析】
(1)由第2层的正方体的个数不同,可得这样的几何体不止一种,再在俯视图的基础上确定每层正方体的数量最多时的正方体的数量,从而可得答案;
(2)在俯视图的基础上确定每层正方体的数量最小时的正方体的数量,从而可得答案.
【详解】
解: (1)这样的几何体不止一种,
正方体最多时的俯视图为:
其中正方形中的数字表示正方体的数量,所以最多需要6+6+2=14个;
(2)最少需要4+4+2=10个,
正方体个数最多时的左视图为:
正方体个数最小时俯视图为:
此时左视图为:
或正方体个数最小时俯视图为:
此时左视图为:
或正方体个数最小时俯视图为:
此时的左视图为:
或正方体个数最小时俯视图为:
此时的左视图为:
或正方体个数最小时俯视图为:
此时的左视图为:
或正方体个数最小时俯视图为:
此时的左视图为:
【点睛】
本题考查的是三视图,掌握三视图的定义,清晰的分类讨论是画图的关键.
4、见解析
【分析】
根据简单几何体的三视图画法画出图形即可.
【详解】
解:三视图如下所示:
【点睛】
本题主要考查了几何体的三视图,解题的关键在于能够熟练掌握画三视图的方法.
5、见解析
【分析】
从正面看:共有3列,从左往右分别有3,1,1个小正方形;从左面看:共有3列,从左往右分别有1,3,1个小正方形;从上面看:共分3列,从左往右分别有3,1,2个小正方形.据此可画出图形.
【详解】
解:如图所示:
【点睛】
本题考查的是画简单组合体的三视图,用到的知识点为:主视图,左视图,俯视图分别是从物体的正面,左面,上面看得到的图形,理解三视图的含义是作图的关键.
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、下面图形是某几何体的三视图(其中主视图也称正视图,左视图也称侧视图),则这个几何体是( )
A.四棱柱 B.四棱锥 C.圆柱 D.圆锥
2、如图是由几个大小相同的小正方体搭成的几何体,若去掉1号小正方体,则下列说法正确的是( )
A.左视图和俯视图不变 B.主视图和左视图不变
C.主视图和俯视图不变 D.都不变
3、如图,图形从三个方向看形状一样的是( )
A. B.
C. D.
4、下列哪种光线形成的投影是平行投影( )
A.太阳 B.探照灯 C.手电筒 D.路灯
5、如图是由5个小立方块搭成的几何体,则该几何体从左面看到的形状图是( )
A. B.
C. D.
6、如图所示的几何体的左视图是( )
A. B. C. D.
7、在下列四幅图形中,能表示两棵小树在同一时刻阳光下影子的图形的可能是( )
A.A B.B C.C D.D
8、全运会颁奖台如图所示,它的主视图是( )
A. B. C. D.
9、下面左侧几何体的主视图是( )
A. B. C. D.
10、下列几何体的主视图和俯视图完全相同的是( )
A. B. C. D.
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题4分,共计20分)
1、如图,AB和DE是直立在地面上的两根立柱,AB=6(m),AB在阳光下的影长BC=3(m),在同一时刻阳光下DE的影长EF=4(m),则DE的长为________米.
2、如图,小亮从一盏9米高的路灯下处向前走了米到达点处时,发现自己在地面上的影子CE是米,则小亮的身高DC为____________米.
3、用小立方体搭一个几何体,分别从它的正面、上面看到的形状如图所示,这样的几何体最少需要 _____个小立方体;最多需要 _____个小立方体.
4、如图,是由若干个完全相同的小正方体组成的一个几何体的主视图和左视图,则组成这个几何体的小正方体的个数最少是_________个.
5、如图是一个几何体的三视图,则这个几何体的表面积为__.
三、解答题(5小题,每小题10分,共计50分)
1、画出几何体的三种视图.
2、如图是由7个棱长为1的小正方体搭成的几何体.
(1)请分别画出这个几何体的主视图、左视图和俯视图;
(2)这个几何体的表面积为 (包括底面积);
(3)若使得该几何体的俯视图和左视图不变,则最多还可以放 个相同的小正方体.
3、用小正方体搭成一个几何体,使得从正面看、从上面看该几何体得到的图形如图所示.问:
(1)这样的几何体只有一种吗?它最多需要多少个小正方体?
(2)它最少需要多少个小正方体?请分别画出这两种情况下从左面看该几何体得到的图形.
4、如图,是由小立方块塔成的几何体,请画出这个几何体从正面、左面、上面三个方面看到的形状图:
5、一个几何体由大小相同的小立方块搭成,箭头所指的为正面,请画出从正面、左面、上面看到的几何体的形状图.
---------参考答案-----------
一、单选题
1、C
【分析】
根据三视图即可完成.
【详解】
此几何体为一个圆柱
故选:C.
【点睛】
本题考查由三视图还原几何体,既要考虑各视图的形状,还要把各视图的情况综合考虑才能得到几何体的形状.
2、A
【分析】
根据从正面看得到的图形是主视图,从左边看得到的图形是左视图,从上边看得到的图形是俯视图,再从看到的小正方形的个数与排列方式两个方面逐一分析可得答案.
【详解】
解:若去掉1号小正方体, 主视图一定变化,主视图中最右边的一列由两个小正方形变为一个,
从上面看过去,看到的小正方形的个数与排列方式不变,所以俯视图不变,
从左边看过去,看到的小正方形的个数与排列方式不变; 所以左视图不变,
所以A符合题意,B,C,D不符合题意;
故选:A.
【点睛】
本题考查的是由小正方体堆砌而成的图形的三视图,掌握“三视图的含义”是解本题的关键.
3、C
【分析】
根据从上面看得到的图形是俯视图,从正面看得到的图形是主视图,从左边看得到的图形是左视图,可得答案.
【详解】
解:A.从上面看是一个圆,从正面和从左边看是一个矩形,故本选项不合题意;
B.从上面看是一个有圆心的圆,从正面和从左边看是一个等腰三角形,故本选项不合题意;
C.从三个方向看形状一样,都是圆形,故本选项符合题意;
D.从上面看是一个正方形,从正面和从左边看是一个长方形形,故本选项不合题意.
故选:C.
【点睛】
本题考查了简单几何体的三视图,从上面看到的图形是俯视图,从正面看到的图形是主视图,从左面看到的图形是左视图.
4、A
【分析】
中心投影是指把光由一点向外散射形成的投影,平行投影是在一束平行光线照射下形成的投影,根据定义逐一分析即可得到答案.
【详解】
解:太阳光线形成的投影是平行投影,
探照灯,手电筒,路灯形成的投影是中心投影,
故选A
【点睛】
本题考查的是平行投影与中心投影的含义及应用,根据定义熟练判断中心投影与平行投影是解题的关键.
5、D
【分析】
左视图:从左边看立体图形,看到的平面图形是左视图,根据左视图的定义可得答案.
【详解】
解:该几何体从左面看到的形状图有2列,
第1列看到1个正方形,第2列看到2个正方形,
所以左视图是D,
故选D
【点睛】
本题考查的是三视图,值得注意的是能看到的立体图形中的线条都要画成实线,看不到的画成虚线,掌握“左视图的含义”是解题的关键.
6、D
【分析】
根据左视图的定义即可得.
【详解】
解:左视图是指从左面观察几何体所得到的视图,
这个几何体的左视图是,
故选:D.
【点睛】
本题考查了左视图,熟记定义是解题关键.
7、D
【分析】
由太阳光是平行光线,可知同一时刻下,影子的朝向一致,由此进行求解即可.
【详解】
解:太阳光是平行光线,因此同一时刻下,影子的朝向是一致的.
故选:D.
【点睛】
考查主要考查了的影子问题,解题的关键在于能够知道太阳光是平行光线.
8、C
【分析】
主视图是从前面先后看得到的图形,根据主视图对各选项一一分析即可.
【详解】
解:主视图是从前面先后看得到的图形,是C.
故选C.
【点睛】
本题考查主视图,掌握三视图的特征是解题关键.
9、A
【分析】
找出从几何体的正面看所得到的图形即可.
【详解】
解:从几何体的正面看,是一行两个并列的矩形.
故选:A.
【点睛】
本题主要考查了几何体的三视图,准确分析判断是解题的关键.
10、D
【分析】
根据主视图和俯视图是分别从物体正面和上面看到的图形,逐项分析即可.
【详解】
解:A、圆柱主视图是矩形,俯视图是圆,故A选项不合题意;
B、圆锥的主视图是等腰三角形,俯视图是圆以及中心有一个点,故B选项不合题意;
C、三棱柱主视图是一行两个矩形且公共边是虚线,俯视图是三角形,故C选项不合题意;
D、圆的主视图和俯视图都为圆,故D选项符合题意;
故选D.
【点睛】
本题考查简单几何体的三视图,解决问题的关键是掌握主视图是从物体的正面看到的视图,俯视图是从物体的上面看得到的视图.
二、填空题
1、8
【解析】
【分析】
连接,,根据平行投影的性质得,根据平行的性质可知,利用相似三角形对应边成比例即可求出的长.
【详解】
解:如图,连接AC ,DF,根据平行投影的性质得DF∥AC,
,
,
,
,
,
.
故答案为:8.
【点睛】
本题主要考查相似三角形的判定和性质,掌握相似三角形的判定定理以及性质是解题的关键.
2、1.8
【解析】
【分析】
同一时刻下物体高度的比等于影长的比,构造相似三角形计算即可.
【详解】
如图,由题意知米,米,米,且,
∴米,
∵,
∴
又∵
∴,
∴,即,
解得(米),即小亮的身高为1.8米;
故答案为:1.8.
【点睛】
本题考查平行投影的相关知识点,能够根据题意构造相似是解题关键点.
3、 10 14
【解析】
【分析】
从上面看中可以看出最底层小正方体的个数及形状,从前面看可以看出每一层小正方体的层数和个数,从而算出总的个数.
【详解】
解:∵从上面看有7个正方形,
∴最底层有7个正方体,
从前面看可得第2层最少有2个正方体;最多有5个正方体,
第3层最少有1个正方体;最多有2个正方体,
∴该组合几何体最少有7+2+1=10个正方体,最多有7+5+2=14个正方体.
故答案为:10,14.
【点睛】
此题主要考查了不同方向看几何体,关键是掌握口诀“上面看打地基,前面看疯狂盖,左面看拆违章”就很容易得到答案.
4、3
【解析】
【分析】
画出模拟俯视图,根据主对列,左对行进行标数,相同取同,不同取0即可得出答案.
【详解】
已知主视图和左视图求堆积几何体最少的情况:画模拟俯视图,主对列,左对行进行标数,相同取同,不同取0.具体如下图:
故答案为:3.
【点睛】
考查学生对三视图的掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,主视图疯狂盖,左视图拆违章”就更容易得到答案.
5、4π
【解析】
【分析】
先判定这个几何体是圆锥,再根据圆锥的特点求出其表面积.
【详解】
解:根据三视图可得这个几何体是圆锥,
底面积=π×12=π,
侧面积为==3π,
则这个几何体的表面积=π+3π=4π;
故答案为:4π.
【点睛】
此题主要考查圆锥的表面积,解题的关键是根据三视图的得到几何体是圆锥.
三、解答题
1、见详解
【分析】
从正面看从左往右3列正方形的个数依次为1,3,2;从左面看从左往右3列正方形的个数依次为3,1;从上面看从左往右3列正方形的个数依次为1,2,1.依此画出图形.
【详解】
解:如图所示:
【点睛】
本题考查了三视图的画法;得到从各个方向看得到的每列正方形的个数是解决本题的关键.
2、(1)见解析;(2)30;(3)3
【分析】
(1)根据三视图的画法画出相应的图形即可;
(2)三视图面积的2倍加被挡住的面积即可;
(3)根据俯视图和左视图的特点即可求解.
【详解】
(1)这个几何体的主视图、左视图和俯视图如下:
(2)(6+4+4)×2+2=30,
故答案为:30;
(3)保持这个几何体的俯视图和左视图不变,可往第一列和第二列分别添加1个、2个小正方体,
故答案为:3.
【点睛】
此题主要考查了三视图,正确掌握不同视图的观察角度是解题关键.
3、(1)不止一种,最多14个;(2)最小10个,画图见解析
【分析】
(1)由第2层的正方体的个数不同,可得这样的几何体不止一种,再在俯视图的基础上确定每层正方体的数量最多时的正方体的数量,从而可得答案;
(2)在俯视图的基础上确定每层正方体的数量最小时的正方体的数量,从而可得答案.
【详解】
解: (1)这样的几何体不止一种,
正方体最多时的俯视图为:
其中正方形中的数字表示正方体的数量,所以最多需要6+6+2=14个;
(2)最少需要4+4+2=10个,
正方体个数最多时的左视图为:
正方体个数最小时俯视图为:
此时左视图为:
或正方体个数最小时俯视图为:
此时左视图为:
或正方体个数最小时俯视图为:
此时的左视图为:
或正方体个数最小时俯视图为:
此时的左视图为:
或正方体个数最小时俯视图为:
此时的左视图为:
或正方体个数最小时俯视图为:
此时的左视图为:
【点睛】
本题考查的是三视图,掌握三视图的定义,清晰的分类讨论是画图的关键.
4、见解析
【分析】
根据简单几何体的三视图画法画出图形即可.
【详解】
解:三视图如下所示:
【点睛】
本题主要考查了几何体的三视图,解题的关键在于能够熟练掌握画三视图的方法.
5、见解析
【分析】
从正面看:共有3列,从左往右分别有3,1,1个小正方形;从左面看:共有3列,从左往右分别有1,3,1个小正方形;从上面看:共分3列,从左往右分别有3,1,2个小正方形.据此可画出图形.
【详解】
解:如图所示:
【点睛】
本题考查的是画简单组合体的三视图,用到的知识点为:主视图,左视图,俯视图分别是从物体的正面,左面,上面看得到的图形,理解三视图的含义是作图的关键.
