湘教版数学八年级下册同步课时作业 1.2 第1课时 勾股定理(word版、含答案)
文档属性
| 名称 | 湘教版数学八年级下册同步课时作业 1.2 第1课时 勾股定理(word版、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 463.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 14:32:46 | ||
图片预览

文档简介
1.2 第1课时 勾股定理
知识点 勾股定理
1.如图,在Rt△ABC中,
∵∠C=90°,
∴AC2+(________)2=(__________)2.(____________)
∵AB=20,BC=16,
∴AC==________.
2.如图,在Rt△ABC中,∠BAC=90°,AB=12,AC=16,D为BC的中点,则线段AD的长为( )
A.6 B.8 C.10 D.12
3.如图,在由边长为1的小正方形组成的网格中,点A,B都在格点上,则线段AB的长度为________.
4.[教材例1变式]如图,在△ABC中,AB=AC,AB=10,BC=16,AD是∠BAC的平分线,交BC于点D,则AD的长为________.
5.如图,∠C=∠ABD=90°,AC=3,BC=4,BD=12,则AD的长为________.
6.教材练习变式在△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c.
(1)若c=61,a=60,求b;
(2)若a=1,∠A=30°,求b;
(3)若c=10,a∶b=3∶4,求a,b.
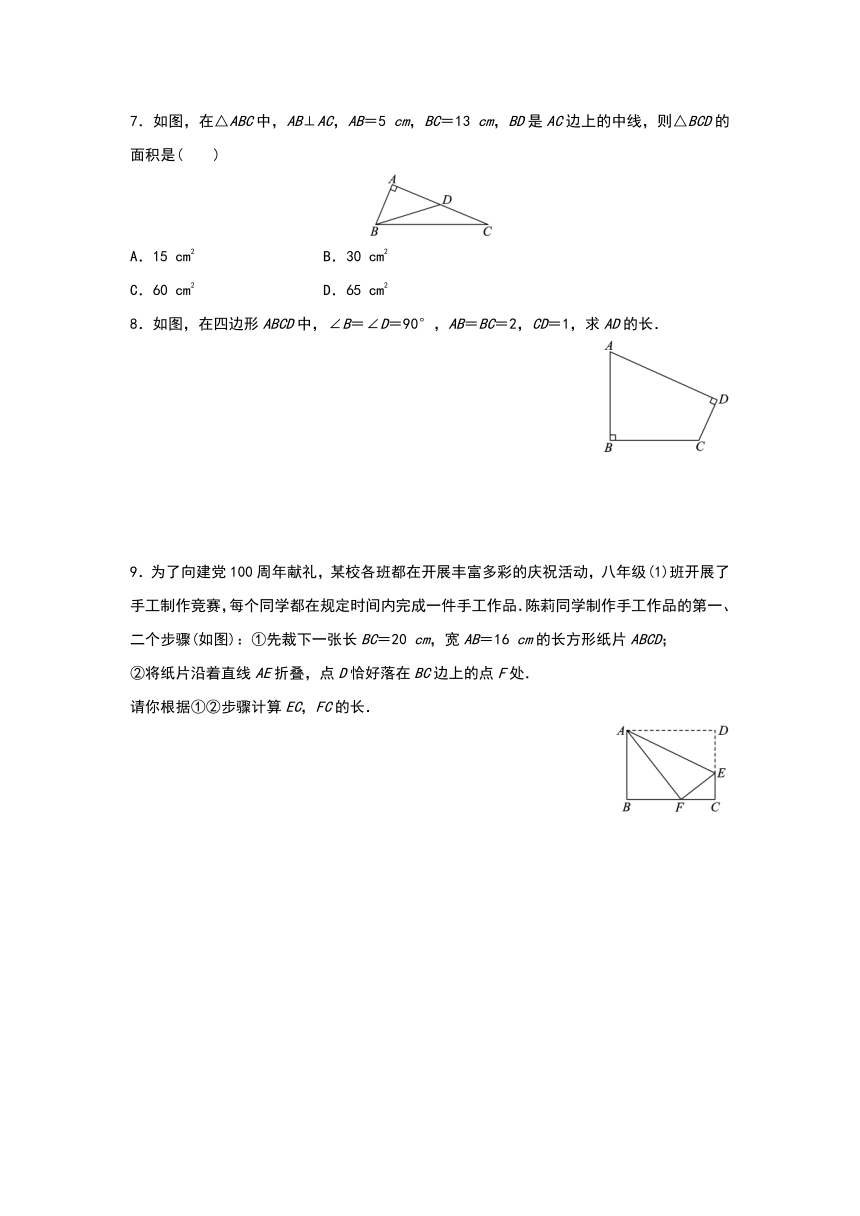
7.如图,在△ABC中,AB⊥AC,AB=5 cm,BC=13 cm,BD是AC边上的中线,则△BCD的面积是( )
A.15 cm2 B.30 cm2
C.60 cm2 D.65 cm2
8.如图,在四边形ABCD中,∠B=∠D=90°,AB=BC=2,CD=1,求AD的长.
9.为了向建党100周年献礼,某校各班都在开展丰富多彩的庆祝活动,八年级(1)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.陈莉同学制作手工作品的第一、二个步骤(如图):①先裁下一张长BC=20 cm,宽AB=16 cm的长方形纸片ABCD;
②将纸片沿着直线AE折叠,点D恰好落在BC边上的点F处.
请你根据①②步骤计算EC,FC的长.
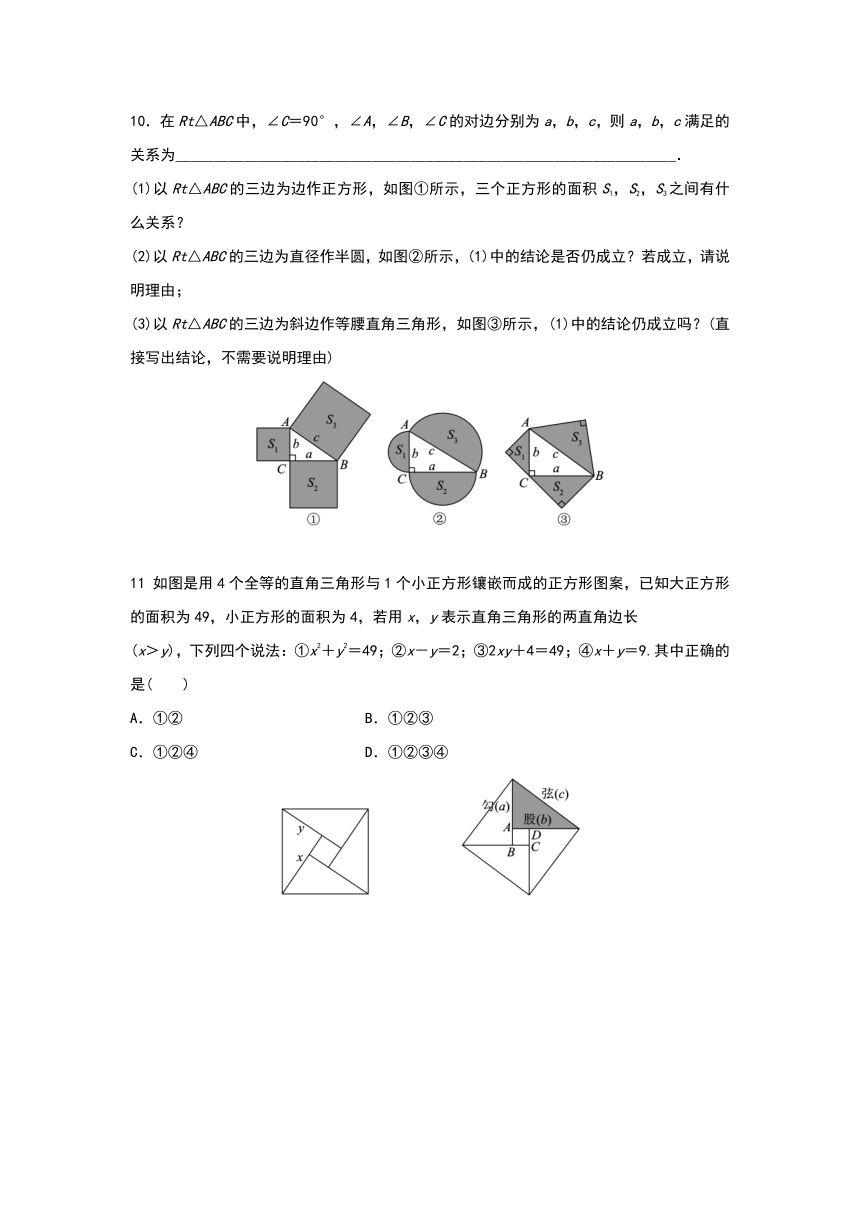
10.在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,则a,b,c满足的关系为__________________________________________________________________.
(1)以Rt△ABC的三边为边作正方形,如图①所示,三个正方形的面积S1,S2,S3之间有什么关系?
(2)以Rt△ABC的三边为直径作半圆,如图②所示,(1)中的结论是否仍成立?若成立,请说明理由;
(3)以Rt△ABC的三边为斜边作等腰直角三角形,如图③所示,(1)中的结论仍成立吗?(直接写出结论,不需要说明理由)
11 如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y表示直角三角形的两直角边长
(x>y),下列四个说法:①x2+y2=49;②x-y=2;③2xy+4=49;④x+y=9.其中正确的是( )
A.①② B.①②③
C.①②④ D.①②③④
12 公元3世纪初,中国古代数学家赵爽注《周髀算经》时,创造了“赵爽弦图”.如图,设勾a=6,弦c=10,则小正方形ABCD的面积是________.
13 如图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.在Rt△ABC中,若直角边AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图②所示的“数学风车”,则这个风车的外围周长(图②中的实线)为________.
1.2 第1课时 勾股定理
1.BC AB 勾股定理 20 16 12
2.C 由勾股定理,得BC==20.∵D为BC的中点,
∴AD=BC=10.
3.5
4.6 ∵AB=AC,AD是∠BAC的平分线,∴AD⊥BC,BD=BC=8.由勾股定理,得AD==6.
5.13 在Rt△ABC中,AC=3,BC=4,根据勾股定理,得AB=5.在Rt△ABD中,AB=5,BD=12,根据勾股定理,得AD=13.
6.解:(1)b===11.
(2)∵在Rt△ABC中,∠C=90°,∠A=30°,a=1,∴c=2a=2.
由a2+b2=c2,得b===.
(3)∵a∶b=3∶4,∴设a=3x,b=4x,
则c=5x.∵c=10,∴x=2,∴a=6,b=8.
7.A 由勾股定理,得AC==12.∵BD是AC边上的中线,∴CD=6,∴△BCD的面积为×5×6=15(cm2).故选A.
8.解:如图,连接AC.
∵∠B=90°,∴AC2=AB2+BC2.
∵AB=BC=2,∴AC2=8.
∵∠D=90°,∴AD2=AC2-CD2=8-12=7,∴AD=(负值已舍去).
9.解:由题意可知△ADE≌△AFE,
∴DE=FE,AD=AF.
∵四边形ABCD是长方形,
∴∠B=∠C=90°,CD=AB=16 cm,AD=BC=20 cm,
∴AF=AD=20 cm.
在Rt△ABF中,由勾股定理,得BF==12(cm),
∴FC=20-12=8(cm).
设EC=x cm,则DE=EF=(16-x)cm.
在Rt△CEF中,由勾股定理,得
(16-x)2=82+x2,解得x=6,
∴EC=6 cm.
10.解:a2+b2=c2
(1)由题意得S1=b2,S2=a2,S3=c2.
∵a2+b2=c2,∴S1+S2=S3.
(2)(1)中的结论仍成立.
理由如下:由题意得S1=·b2,S2=·a2,S3=·c2.
∵a2+b2=c2,∴S1+S2=S3,
即(1)中的结论仍成立.
(3)(1)中的结论仍成立.
11 B 如图,因为大正方形的面积为49,小正方形的面积为4,所以AB2=49,
EF2=4,所以AB=7,EF=2.在Rt△ABE中,由勾股定理,知x2+y2=49,故①正确.由EF=2,知x-y=2,故②正确.由(x-y)2=4,知2xy+4=x2+y2=49,故③正确.由③,知4xy=90.又因为(x+y)2=(x-y)2+4xy,所以(x+y)2=4+90=94,所以x+y=,故④不正确.综上所述,正确的说法为①②③.故选B.
12 4 ∵勾a=6,弦c=10,∴股b==8,
∴小正方形的边长为8-6=2,∴小正方形的面积为22=4.故答案是4.
13 76 如图所示,由题意得,DB=BF=6,EF=5,∴DF=12,
∴DE===13,∴所以这个风车的外围周长为4(DB+DE)=4×19=76.
知识点 勾股定理
1.如图,在Rt△ABC中,
∵∠C=90°,
∴AC2+(________)2=(__________)2.(____________)
∵AB=20,BC=16,
∴AC==________.
2.如图,在Rt△ABC中,∠BAC=90°,AB=12,AC=16,D为BC的中点,则线段AD的长为( )
A.6 B.8 C.10 D.12
3.如图,在由边长为1的小正方形组成的网格中,点A,B都在格点上,则线段AB的长度为________.
4.[教材例1变式]如图,在△ABC中,AB=AC,AB=10,BC=16,AD是∠BAC的平分线,交BC于点D,则AD的长为________.
5.如图,∠C=∠ABD=90°,AC=3,BC=4,BD=12,则AD的长为________.
6.教材练习变式在△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c.
(1)若c=61,a=60,求b;
(2)若a=1,∠A=30°,求b;
(3)若c=10,a∶b=3∶4,求a,b.
7.如图,在△ABC中,AB⊥AC,AB=5 cm,BC=13 cm,BD是AC边上的中线,则△BCD的面积是( )
A.15 cm2 B.30 cm2
C.60 cm2 D.65 cm2
8.如图,在四边形ABCD中,∠B=∠D=90°,AB=BC=2,CD=1,求AD的长.
9.为了向建党100周年献礼,某校各班都在开展丰富多彩的庆祝活动,八年级(1)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.陈莉同学制作手工作品的第一、二个步骤(如图):①先裁下一张长BC=20 cm,宽AB=16 cm的长方形纸片ABCD;
②将纸片沿着直线AE折叠,点D恰好落在BC边上的点F处.
请你根据①②步骤计算EC,FC的长.
10.在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,则a,b,c满足的关系为__________________________________________________________________.
(1)以Rt△ABC的三边为边作正方形,如图①所示,三个正方形的面积S1,S2,S3之间有什么关系?
(2)以Rt△ABC的三边为直径作半圆,如图②所示,(1)中的结论是否仍成立?若成立,请说明理由;
(3)以Rt△ABC的三边为斜边作等腰直角三角形,如图③所示,(1)中的结论仍成立吗?(直接写出结论,不需要说明理由)
11 如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形的面积为49,小正方形的面积为4,若用x,y表示直角三角形的两直角边长
(x>y),下列四个说法:①x2+y2=49;②x-y=2;③2xy+4=49;④x+y=9.其中正确的是( )
A.①② B.①②③
C.①②④ D.①②③④
12 公元3世纪初,中国古代数学家赵爽注《周髀算经》时,创造了“赵爽弦图”.如图,设勾a=6,弦c=10,则小正方形ABCD的面积是________.
13 如图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.在Rt△ABC中,若直角边AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图②所示的“数学风车”,则这个风车的外围周长(图②中的实线)为________.
1.2 第1课时 勾股定理
1.BC AB 勾股定理 20 16 12
2.C 由勾股定理,得BC==20.∵D为BC的中点,
∴AD=BC=10.
3.5
4.6 ∵AB=AC,AD是∠BAC的平分线,∴AD⊥BC,BD=BC=8.由勾股定理,得AD==6.
5.13 在Rt△ABC中,AC=3,BC=4,根据勾股定理,得AB=5.在Rt△ABD中,AB=5,BD=12,根据勾股定理,得AD=13.
6.解:(1)b===11.
(2)∵在Rt△ABC中,∠C=90°,∠A=30°,a=1,∴c=2a=2.
由a2+b2=c2,得b===.
(3)∵a∶b=3∶4,∴设a=3x,b=4x,
则c=5x.∵c=10,∴x=2,∴a=6,b=8.
7.A 由勾股定理,得AC==12.∵BD是AC边上的中线,∴CD=6,∴△BCD的面积为×5×6=15(cm2).故选A.
8.解:如图,连接AC.
∵∠B=90°,∴AC2=AB2+BC2.
∵AB=BC=2,∴AC2=8.
∵∠D=90°,∴AD2=AC2-CD2=8-12=7,∴AD=(负值已舍去).
9.解:由题意可知△ADE≌△AFE,
∴DE=FE,AD=AF.
∵四边形ABCD是长方形,
∴∠B=∠C=90°,CD=AB=16 cm,AD=BC=20 cm,
∴AF=AD=20 cm.
在Rt△ABF中,由勾股定理,得BF==12(cm),
∴FC=20-12=8(cm).
设EC=x cm,则DE=EF=(16-x)cm.
在Rt△CEF中,由勾股定理,得
(16-x)2=82+x2,解得x=6,
∴EC=6 cm.
10.解:a2+b2=c2
(1)由题意得S1=b2,S2=a2,S3=c2.
∵a2+b2=c2,∴S1+S2=S3.
(2)(1)中的结论仍成立.
理由如下:由题意得S1=·b2,S2=·a2,S3=·c2.
∵a2+b2=c2,∴S1+S2=S3,
即(1)中的结论仍成立.
(3)(1)中的结论仍成立.
11 B 如图,因为大正方形的面积为49,小正方形的面积为4,所以AB2=49,
EF2=4,所以AB=7,EF=2.在Rt△ABE中,由勾股定理,知x2+y2=49,故①正确.由EF=2,知x-y=2,故②正确.由(x-y)2=4,知2xy+4=x2+y2=49,故③正确.由③,知4xy=90.又因为(x+y)2=(x-y)2+4xy,所以(x+y)2=4+90=94,所以x+y=,故④不正确.综上所述,正确的说法为①②③.故选B.
12 4 ∵勾a=6,弦c=10,∴股b==8,
∴小正方形的边长为8-6=2,∴小正方形的面积为22=4.故答案是4.
13 76 如图所示,由题意得,DB=BF=6,EF=5,∴DF=12,
∴DE===13,∴所以这个风车的外围周长为4(DB+DE)=4×19=76.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
