湘教版数学八年级下册同步课时作业 1.4 第2课时 角平分线的性质的综合应用(word版、含答案)
文档属性
| 名称 | 湘教版数学八年级下册同步课时作业 1.4 第2课时 角平分线的性质的综合应用(word版、含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 667.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 14:40:57 | ||
图片预览



文档简介
第2课时 角平分线的性质的综合应用
知识点 角平分线性质的综合应用
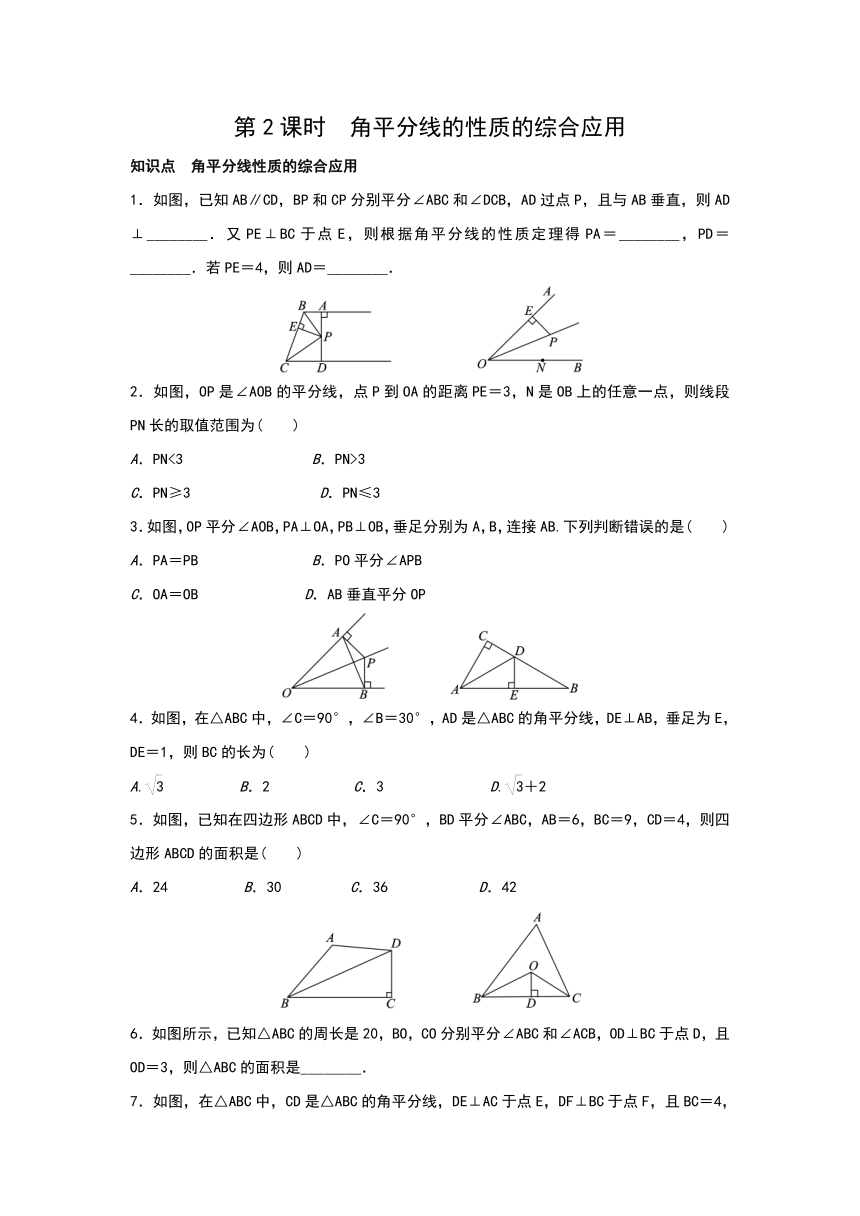
1.如图,已知AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直,则AD⊥________.又PE⊥BC于点E,则根据角平分线的性质定理得PA=________,PD=________.若PE=4,则AD=________.
2.如图,OP是∠AOB的平分线,点P到OA的距离PE=3,N是OB上的任意一点,则线段PN长的取值范围为( )
A.PN<3 B.PN>3
C.PN≥3 D.PN≤3
3.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B,连接AB.下列判断错误的是( )
A.PA=PB B.PO平分∠APB
C.OA=OB D.AB垂直平分OP
4.如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=1,则BC的长为( )
A. B.2 C.3 D.+2
5.如图,已知在四边形ABCD中,∠C=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是( )
A.24 B.30 C.36 D.42
6.如图所示,已知△ABC的周长是20,BO,CO分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,则△ABC的面积是________.
7.如图,在△ABC中,CD是△ABC的角平分线,DE⊥AC于点E,DF⊥BC于点F,且BC=4,DE=2,则△BCD的面积是________.
8.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于点C.若EC=1,则OF=________.
9.如图,在四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.
求证:(1)AM⊥DM;
(2)M为BC的中点.
10.如图,在四边形ABCD中,AB=CD,BA和CD的延长线交于点E.若点P使得S△PAB=S△PCD,则满足此条件的点P( )
A.有且只有1个
B.有且只有2个
C.组成∠E的平分线
D.组成∠E的平分线所在的直线(点E除外)
11.如图,O是△ABC内的一点,且点O到三边AB,BC,CA的距离相等.若∠BAC=70°,则∠BOC的度数为( )
A.70° B.120° C.125° D.130°
12.如图,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于点S,有下列三个结论:①AS=AR;②QP∥AR;③△BPR≌△QPS.其中正确的是( )
A.①②③ B.①②
C.① D.①③
13.如图,直线a,b,c表示三条互相交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
A.一处 B.两处
C.三处 D.四处
14.已知:如图所示,AB=AC,BD=CD,DE⊥AB交AB的延长线于点E,DF⊥AC交AC的延长线于点F.求证:DE=DF.
15.已知∠MAN=120°,AC平分∠MAN,点B,D分别在AN,AM上.
(1)如图①,若∠ABC=∠ADC=90°,请你探索线段AD,AB,AC之间的数量关系,并证明.
(2)如图②,若∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
第2课时 角平分线的性质的综合应用
1.CD PE PE 8
2.C 如图,过点P作PM⊥OB于点M.
∵OP是∠AOB的平分线,PE⊥OA,PM⊥OB,
∴PM=PE=3,∴PN≥3.
故选C.
3.D
4.C
5.B 如图,过点D作DH⊥AB交BA的延长线于点H.
∵BD平分∠ABC,∠C=90°,DH⊥AB,
∴DH=CD=4,
∴S四边形ABCD=S△ABD+S△BCD=AB·DH+BC·CD=×6×4+×9×4=30.
故选B.
6.30
7.4 ∵CD是△ABC的角平分线,DE⊥AC于点E,DF⊥BC于点F,且DE=2,
∴DF=2,∴△BCD的面积为×2×4=4.
故填4.
8.2 如图,过点E作EH⊥OA于点H.
∵∠AOE=∠BOE=15°,EC⊥OB于点C,EH⊥OA于点H,
∴EH=EC=1,∠AOB=30°.
∵EF∥OB,
∴∠EFH=∠AOB=30°,∠FEO=∠BOE,
∴EF=2EH=2,∠FEO=∠FOE,
∴OF=EF=2.
9.证明:(1)∵AB∥CD,
∴∠BAD+∠ADC=180°.
∵AM平分∠BAD,DM平分∠ADC,
∴2∠MAD+2∠ADM=180°,
∴∠MAD+∠ADM=90°,
∴∠AMD=90°,即AM⊥DM.
(2)如图,过点M作MN⊥AD于点N.
∵∠B=90°,AB∥CD,∴BM⊥AB,CM⊥CD.
又∵AM平分∠BAD,DM平分∠ADC,MN⊥AD,
∴BM=MN,MN=CM,
∴BM=CM,即M为BC的中点.
10.D ∵AB=CD,S△PAB=S△PCD,∴只需使这两个三角形中AB,CD边上的高相等即可,显然这样的点组成∠E的平分线所在的直线(点E除外).
11.C 12.B
13.D 由三角形内角平分线的交点到三角形三边的距离相等,可得三角形内角平分线的交点满足题意;然后利用角平分线的性质,可证得三角形两条外角平分线的交点到其三边的距离也相等,这样的点共有三个,所以可供选择的地址有四处.
14.证明:如图所示,连接AD.
在△ABD和△ACD中,
∴△ABD≌△ACD(SSS),
∴∠EAD=∠FAD,即AD平分∠EAF.
又∵DE⊥AB,DF⊥AC,∴DE=DF.
15.解:(1)AD+AB=AC.
证明:∵AC平分∠MAN,∠MAN=120°,
∴∠CAD=∠CAB=60°.
又∵∠ADC=∠ABC=90°,
∴∠ACD=∠ACB=30°,
则AD=AB=AC(直角三角形中30°角所对的直角边等于斜边的一半),
∴AD+AB=AC.
(2)仍成立.
证明:如图,过点C分别作AM,AN的垂线,垂足分别为E,F.
∵AC平分∠MAN,CE⊥AM,CF⊥AN,
∴CE=CF(角平分线上的点到角两边的距离相等).
∵∠ABC+∠ADC=180°,∠ADC+∠CDE=180°,
∴∠CDE=∠ABC.
又∵∠CED=∠CFB=90°,CE=CF,
∴△CED≌△CFB(AAS),
∴ED=FB,
∴AD+AB=AE-ED+AF+FB=AE+AF.
由(1)知AE+AF=AC,
∴AD+AB=AC.
知识点 角平分线性质的综合应用
1.如图,已知AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直,则AD⊥________.又PE⊥BC于点E,则根据角平分线的性质定理得PA=________,PD=________.若PE=4,则AD=________.
2.如图,OP是∠AOB的平分线,点P到OA的距离PE=3,N是OB上的任意一点,则线段PN长的取值范围为( )
A.PN<3 B.PN>3
C.PN≥3 D.PN≤3
3.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B,连接AB.下列判断错误的是( )
A.PA=PB B.PO平分∠APB
C.OA=OB D.AB垂直平分OP
4.如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=1,则BC的长为( )
A. B.2 C.3 D.+2
5.如图,已知在四边形ABCD中,∠C=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是( )
A.24 B.30 C.36 D.42
6.如图所示,已知△ABC的周长是20,BO,CO分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,则△ABC的面积是________.
7.如图,在△ABC中,CD是△ABC的角平分线,DE⊥AC于点E,DF⊥BC于点F,且BC=4,DE=2,则△BCD的面积是________.
8.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于点C.若EC=1,则OF=________.
9.如图,在四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.
求证:(1)AM⊥DM;
(2)M为BC的中点.
10.如图,在四边形ABCD中,AB=CD,BA和CD的延长线交于点E.若点P使得S△PAB=S△PCD,则满足此条件的点P( )
A.有且只有1个
B.有且只有2个
C.组成∠E的平分线
D.组成∠E的平分线所在的直线(点E除外)
11.如图,O是△ABC内的一点,且点O到三边AB,BC,CA的距离相等.若∠BAC=70°,则∠BOC的度数为( )
A.70° B.120° C.125° D.130°
12.如图,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于点S,有下列三个结论:①AS=AR;②QP∥AR;③△BPR≌△QPS.其中正确的是( )
A.①②③ B.①②
C.① D.①③
13.如图,直线a,b,c表示三条互相交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
A.一处 B.两处
C.三处 D.四处
14.已知:如图所示,AB=AC,BD=CD,DE⊥AB交AB的延长线于点E,DF⊥AC交AC的延长线于点F.求证:DE=DF.
15.已知∠MAN=120°,AC平分∠MAN,点B,D分别在AN,AM上.
(1)如图①,若∠ABC=∠ADC=90°,请你探索线段AD,AB,AC之间的数量关系,并证明.
(2)如图②,若∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
第2课时 角平分线的性质的综合应用
1.CD PE PE 8
2.C 如图,过点P作PM⊥OB于点M.
∵OP是∠AOB的平分线,PE⊥OA,PM⊥OB,
∴PM=PE=3,∴PN≥3.
故选C.
3.D
4.C
5.B 如图,过点D作DH⊥AB交BA的延长线于点H.
∵BD平分∠ABC,∠C=90°,DH⊥AB,
∴DH=CD=4,
∴S四边形ABCD=S△ABD+S△BCD=AB·DH+BC·CD=×6×4+×9×4=30.
故选B.
6.30
7.4 ∵CD是△ABC的角平分线,DE⊥AC于点E,DF⊥BC于点F,且DE=2,
∴DF=2,∴△BCD的面积为×2×4=4.
故填4.
8.2 如图,过点E作EH⊥OA于点H.
∵∠AOE=∠BOE=15°,EC⊥OB于点C,EH⊥OA于点H,
∴EH=EC=1,∠AOB=30°.
∵EF∥OB,
∴∠EFH=∠AOB=30°,∠FEO=∠BOE,
∴EF=2EH=2,∠FEO=∠FOE,
∴OF=EF=2.
9.证明:(1)∵AB∥CD,
∴∠BAD+∠ADC=180°.
∵AM平分∠BAD,DM平分∠ADC,
∴2∠MAD+2∠ADM=180°,
∴∠MAD+∠ADM=90°,
∴∠AMD=90°,即AM⊥DM.
(2)如图,过点M作MN⊥AD于点N.
∵∠B=90°,AB∥CD,∴BM⊥AB,CM⊥CD.
又∵AM平分∠BAD,DM平分∠ADC,MN⊥AD,
∴BM=MN,MN=CM,
∴BM=CM,即M为BC的中点.
10.D ∵AB=CD,S△PAB=S△PCD,∴只需使这两个三角形中AB,CD边上的高相等即可,显然这样的点组成∠E的平分线所在的直线(点E除外).
11.C 12.B
13.D 由三角形内角平分线的交点到三角形三边的距离相等,可得三角形内角平分线的交点满足题意;然后利用角平分线的性质,可证得三角形两条外角平分线的交点到其三边的距离也相等,这样的点共有三个,所以可供选择的地址有四处.
14.证明:如图所示,连接AD.
在△ABD和△ACD中,
∴△ABD≌△ACD(SSS),
∴∠EAD=∠FAD,即AD平分∠EAF.
又∵DE⊥AB,DF⊥AC,∴DE=DF.
15.解:(1)AD+AB=AC.
证明:∵AC平分∠MAN,∠MAN=120°,
∴∠CAD=∠CAB=60°.
又∵∠ADC=∠ABC=90°,
∴∠ACD=∠ACB=30°,
则AD=AB=AC(直角三角形中30°角所对的直角边等于斜边的一半),
∴AD+AB=AC.
(2)仍成立.
证明:如图,过点C分别作AM,AN的垂线,垂足分别为E,F.
∵AC平分∠MAN,CE⊥AM,CF⊥AN,
∴CE=CF(角平分线上的点到角两边的距离相等).
∵∠ABC+∠ADC=180°,∠ADC+∠CDE=180°,
∴∠CDE=∠ABC.
又∵∠CED=∠CFB=90°,CE=CF,
∴△CED≌△CFB(AAS),
∴ED=FB,
∴AD+AB=AE-ED+AF+FB=AE+AF.
由(1)知AE+AF=AC,
∴AD+AB=AC.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
