湘教版数学八年级下册 2.1 第2课时 多边形的外角和 同步课时作业(word版含答案)
文档属性
| 名称 | 湘教版数学八年级下册 2.1 第2课时 多边形的外角和 同步课时作业(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 375.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 14:43:39 | ||
图片预览

文档简介
第2课时 多边形的外角和
知识点 1 多边形的外角和
1.正十边形的外角和为( )
A.180° B.360°
C.720° D.1440°
2.如果一个多边形的内角和是外角和的5倍,那么这个多边形的边数是( )
A.10 B.11 C.12 D.13
3.若一个多边形的内角和等于它的外角和,则这个多边形的边数为________.
4.若一个正多边形的内角和为540°,则这个正多边形的任意一个外角为________°.
5.如果一个正多边形的每个外角均为60°,那么这个正多边形的内角和是________.
6.若一个多边形的内角和与外角和之和是900°,则该多边形的边数是________.
7.若一个多边形的内角和与外角和之比为9∶2,求这个多边形的边数.
知识点 2 四边形的不稳定性
8.下列图形具有稳定性的是( )
9.四边形具有不稳定性,当一个四边形只有形状改变时,下列发生变化的是( )
A.四边形的边长
B.四边形的周长
C.四边形的某些角的大小
D.四边形的内角和
10.可伸缩的遮阳篷是依据四边形的( )
A.不稳定性 B.稳定性
C.伸缩性 D.可变性
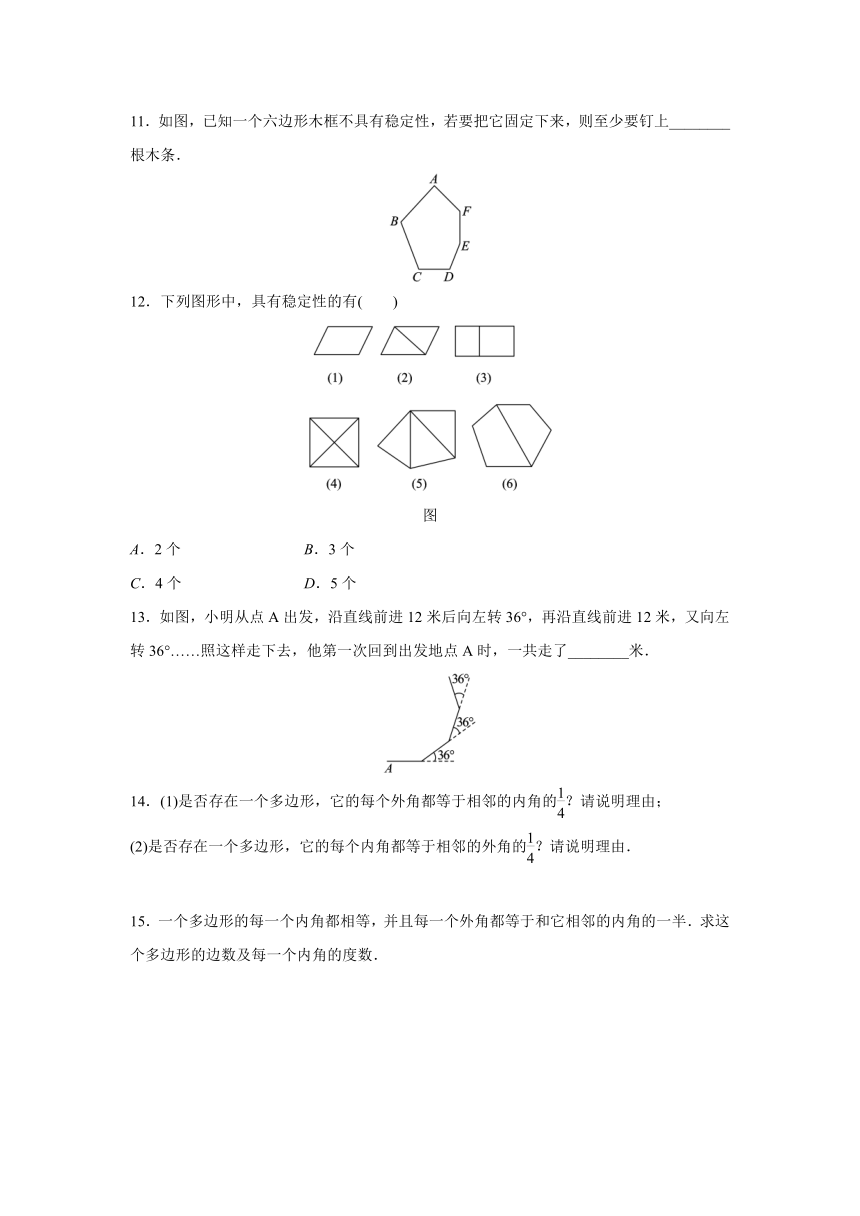
11.如图,已知一个六边形木框不具有稳定性,若要把它固定下来,则至少要钉上________根木条.
12.下列图形中,具有稳定性的有( )
图
A.2个 B.3个
C.4个 D.5个
13.如图,小明从点A出发,沿直线前进12米后向左转36°,再沿直线前进12米,又向左转36°……照这样走下去,他第一次回到出发地点A时,一共走了________米.
14.(1)是否存在一个多边形,它的每个外角都等于相邻的内角的?请说明理由;
(2)是否存在一个多边形,它的每个内角都等于相邻的外角的?请说明理由.
15.一个多边形的每一个内角都相等,并且每一个外角都等于和它相邻的内角的一半.求这个多边形的边数及每一个内角的度数.
16.已知多边形的内角和与某一个外角的度数总和为1350°.
(1)求此多边形的边数;
(2)此多边形必有一内角为多少度?
17.如图所示,小明家有一个由六条钢管连接而成的钢架ABCDEF,为了使这一钢架稳固,他计划在钢架的内部用三根钢管连接使它不变形,请帮助小明解决这个问题.(画图说明,用三种不同的方法)
第2课时 多边形的外角和
1.B 2.C
3.4 [解析] 设多边形的边数为n,则(n-2)·180°=360°,解得n=4.故答案为4.
4.72 [解析] 设此正多边形为正n边形.根据题意,得(n-2)·180°=540°,解得n=5,故这个正多边形的任意一个外角为=72°.
5.720°
6.5
7.解:∵多边形的内角和与外角和之比为9∶2,任何一个多边形的外角和都等于360°,
∴此多边形的内角和为360°÷2×9=1620°.
设这个多边形的边数为n,
则(n-2)·180°=1620°,
解得n=11.
故这个多边形的边数为11.
8.A
9.C
10.A
11.3
12.B [解析] 具有稳定性的是(2)(4)(5).
13.120 [解析] 因为360°÷36°=10,所以他走的路径是一个正十边形,所以他第一次回到出发地点A时,一共走了12×10=120(米).
14.解:(1)存在.理由:
设该多边形的每个外角都是x°,则它的每个内角都是4x°.
由题意,得x+4x=180,
解得x=36,
∴多边形的边数是360÷36=10,
∴存在十边形,它的每个外角都等于相邻的内角的.
(2)不存在.理由:
∵多边形的外角和为360°,∴由题意得内角和为360°×=90°.
∵90°不是180°的整数倍,
∴不存在一个多边形,它的每个内角都等于相邻的外角的.
15.解:设这个多边形的每一个内角为x,则每一个外角为x.
由题意,得x+x=180°,
解得x=120°,则x=×120°=60°,
∴这个多边形的边数为=6.
答:这个多边形的边数为6,每一个内角的度数是120°.
16.解:(1)设此多边形的边数为n,这个外角为x°,则0<x<180.
根据题意,得
(n-2)·180+x=1350,
∴n=+2=9+.
∵n为正整数,
∴90-x必为180的整数倍.
又∵0<x<180,∴90-x=0,∴x=90,
∴n=9,即此多边形的边数为9.
(2)由(1)知此多边形必有一内角为180°-90°=90°.
17.解:答案不唯一,如图.
知识点 1 多边形的外角和
1.正十边形的外角和为( )
A.180° B.360°
C.720° D.1440°
2.如果一个多边形的内角和是外角和的5倍,那么这个多边形的边数是( )
A.10 B.11 C.12 D.13
3.若一个多边形的内角和等于它的外角和,则这个多边形的边数为________.
4.若一个正多边形的内角和为540°,则这个正多边形的任意一个外角为________°.
5.如果一个正多边形的每个外角均为60°,那么这个正多边形的内角和是________.
6.若一个多边形的内角和与外角和之和是900°,则该多边形的边数是________.
7.若一个多边形的内角和与外角和之比为9∶2,求这个多边形的边数.
知识点 2 四边形的不稳定性
8.下列图形具有稳定性的是( )
9.四边形具有不稳定性,当一个四边形只有形状改变时,下列发生变化的是( )
A.四边形的边长
B.四边形的周长
C.四边形的某些角的大小
D.四边形的内角和
10.可伸缩的遮阳篷是依据四边形的( )
A.不稳定性 B.稳定性
C.伸缩性 D.可变性
11.如图,已知一个六边形木框不具有稳定性,若要把它固定下来,则至少要钉上________根木条.
12.下列图形中,具有稳定性的有( )
图
A.2个 B.3个
C.4个 D.5个
13.如图,小明从点A出发,沿直线前进12米后向左转36°,再沿直线前进12米,又向左转36°……照这样走下去,他第一次回到出发地点A时,一共走了________米.
14.(1)是否存在一个多边形,它的每个外角都等于相邻的内角的?请说明理由;
(2)是否存在一个多边形,它的每个内角都等于相邻的外角的?请说明理由.
15.一个多边形的每一个内角都相等,并且每一个外角都等于和它相邻的内角的一半.求这个多边形的边数及每一个内角的度数.
16.已知多边形的内角和与某一个外角的度数总和为1350°.
(1)求此多边形的边数;
(2)此多边形必有一内角为多少度?
17.如图所示,小明家有一个由六条钢管连接而成的钢架ABCDEF,为了使这一钢架稳固,他计划在钢架的内部用三根钢管连接使它不变形,请帮助小明解决这个问题.(画图说明,用三种不同的方法)
第2课时 多边形的外角和
1.B 2.C
3.4 [解析] 设多边形的边数为n,则(n-2)·180°=360°,解得n=4.故答案为4.
4.72 [解析] 设此正多边形为正n边形.根据题意,得(n-2)·180°=540°,解得n=5,故这个正多边形的任意一个外角为=72°.
5.720°
6.5
7.解:∵多边形的内角和与外角和之比为9∶2,任何一个多边形的外角和都等于360°,
∴此多边形的内角和为360°÷2×9=1620°.
设这个多边形的边数为n,
则(n-2)·180°=1620°,
解得n=11.
故这个多边形的边数为11.
8.A
9.C
10.A
11.3
12.B [解析] 具有稳定性的是(2)(4)(5).
13.120 [解析] 因为360°÷36°=10,所以他走的路径是一个正十边形,所以他第一次回到出发地点A时,一共走了12×10=120(米).
14.解:(1)存在.理由:
设该多边形的每个外角都是x°,则它的每个内角都是4x°.
由题意,得x+4x=180,
解得x=36,
∴多边形的边数是360÷36=10,
∴存在十边形,它的每个外角都等于相邻的内角的.
(2)不存在.理由:
∵多边形的外角和为360°,∴由题意得内角和为360°×=90°.
∵90°不是180°的整数倍,
∴不存在一个多边形,它的每个内角都等于相邻的外角的.
15.解:设这个多边形的每一个内角为x,则每一个外角为x.
由题意,得x+x=180°,
解得x=120°,则x=×120°=60°,
∴这个多边形的边数为=6.
答:这个多边形的边数为6,每一个内角的度数是120°.
16.解:(1)设此多边形的边数为n,这个外角为x°,则0<x<180.
根据题意,得
(n-2)·180+x=1350,
∴n=+2=9+.
∵n为正整数,
∴90-x必为180的整数倍.
又∵0<x<180,∴90-x=0,∴x=90,
∴n=9,即此多边形的边数为9.
(2)由(1)知此多边形必有一内角为180°-90°=90°.
17.解:答案不唯一,如图.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
