湘教版数学八年级下册 2.2.2 第1课时 平行四边形的判定定理1,2 同步课时作业(word版含答案)
文档属性
| 名称 | 湘教版数学八年级下册 2.2.2 第1课时 平行四边形的判定定理1,2 同步课时作业(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 284.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 00:00:00 | ||
图片预览


文档简介
2.2.2 第1课时 平行四边形的判定定理1,2
知识点 1 一组对边平行且相等的四边形是平行四边形
1.在四边形ABCD中,AB∥CD,AB=CD,则四边形ABCD为__________四边形,理由是____________________________________________________________________________.
2.下列不能判定四边形ABCD是平行四边形的是( )
A.AB∥CD,AD∥BC
B.CD∥AB,CD=AB
C.BC∥AD,AB=CD
D.AD∥BC,AD=BC
3.如图,在四边形ABCD中,AD=BC,∠ACB=∠CAD.求证:AB=CD.
4.[2020岳阳]如图,点E,F分别在 ABCD的边BC,AD上,BE=BC,FD=
AD,连接BF,DE.求证:四边形BEDF是平行四边形.
知识点 2 两组对边分别相等的四边形是平行四边形
5.在四边形ABCD中,AB=7 cm,BC=5 cm,当CD=________ cm,AD=________cm时,四边形ABCD是平行四边形.
6.如图,在四边形ABCD中,AB=DC,BC=AD.若∠C=120°,则∠A=________°.
7.如图,在 ABCD中,E,F,G,H分别是AB,BC,CD,DA边上的点,
AE=CG,DH=BF,连接EF,FG,GH,HE.
求证:四边形EFGH是平行四边形.
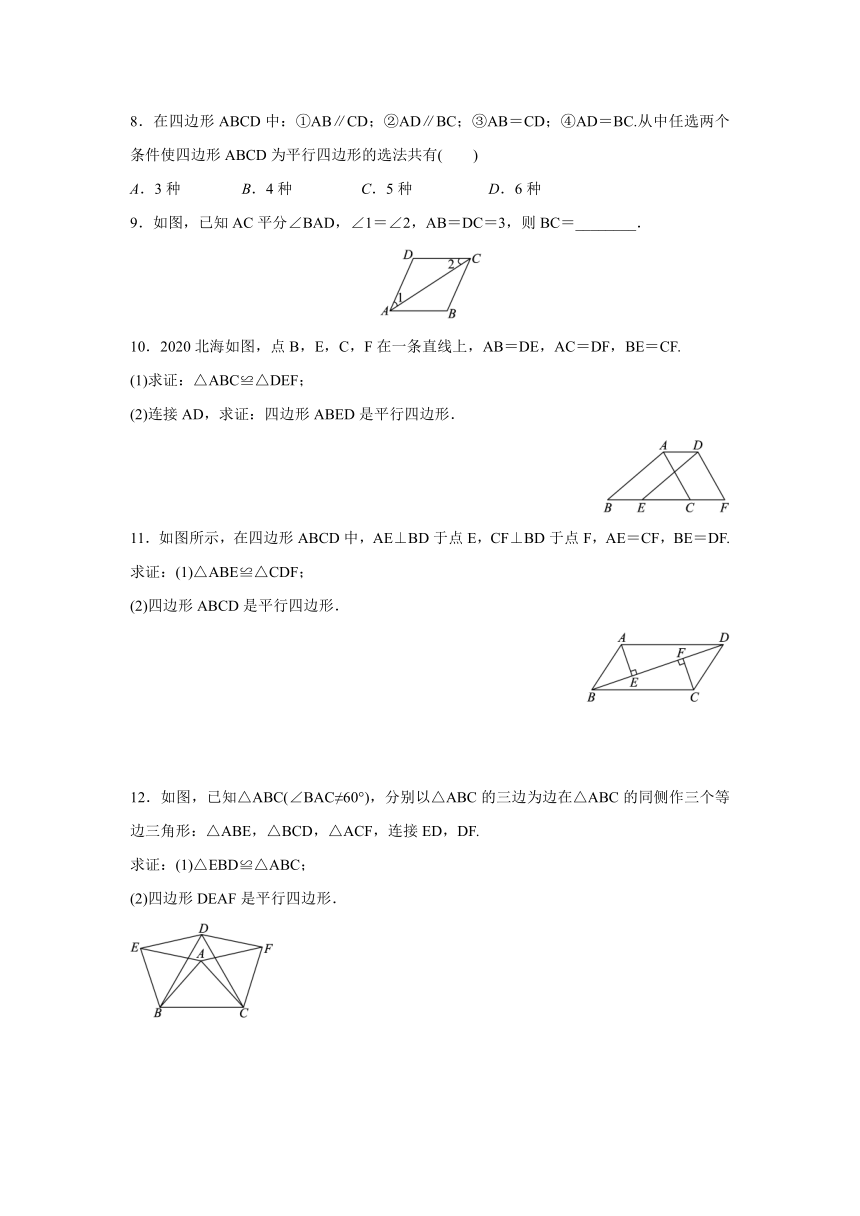
8.在四边形ABCD中:①AB∥CD;②AD∥BC;③AB=CD;④AD=BC.从中任选两个条件使四边形ABCD为平行四边形的选法共有( )
A.3种 B.4种 C.5种 D.6种
9.如图,已知AC平分∠BAD,∠1=∠2,AB=DC=3,则BC=________.
10.2020北海如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.
(1)求证:△ABC≌△DEF;
(2)连接AD,求证:四边形ABED是平行四边形.
11.如图所示,在四边形ABCD中,AE⊥BD于点E,CF⊥BD于点F,AE=CF,BE=DF.
求证:(1)△ABE≌△CDF;
(2)四边形ABCD是平行四边形.
12.如图,已知△ABC(∠BAC≠60°),分别以△ABC的三边为边在△ABC的同侧作三个等边三角形:△ABE,△BCD,△ACF,连接ED,DF.
求证:(1)△EBD≌△ABC;
(2)四边形DEAF是平行四边形.
13.如图所示,在四边形ABCD中,AD∥BC,BC=6厘米,AD=9厘米,点P,Q分别从点A,C同时出发,点P以1厘米/秒的速度由点A向终点D运动,点Q以2厘米/秒的速度由点C向终点B运动,当一点到达终点时,两点同时停止运动.
(1)运动几秒时,四边形ABQP为平行四边形?
(2)运动几秒时,直线PQ将四边形ABCD截出一个平行四边形?
2.2.2 第1课时 平行四边形的判定定理1, 2
1.平行 一组对边平行且相等的四边形是平行四边形
2.C
3.证明:∵∠ACB=∠CAD,
∴AD∥BC.
又∵AD=BC,
∴四边形ABCD是平行四边形,
∴AB=CD.
4.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC.
∵BE=BC,FD=AD,∴BE=FD.
又∵BE∥FD,∴四边形BEDF是平行四边形.
5.7 5 [解析] 根据两组对边分别相等的四边形是平行四边形可得答案.
6.120
7.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,∠A=∠C,∠B=∠D.
∵AE=CG,DH=BF,
∴AD-DH=BC-BF,AB-AE=CD-CG,
即AH=CF,BE=DG.
在△AEH和△CGF中,
∴△AEH≌△CGF(SAS),∴EH=GF.
在△EBF和△GDH中,
∴△EBF≌△GDH(SAS),
∴EF=GH,
∴四边形EFGH是平行四边形.
8.B [解析] 平行四边形的定义:两组对边分别平行的四边形是平行四边形:①②;平行四边形的判定定理2:两组对边分别相等的四边形是平行四边形:③④;平行四边形的判定定理1:一组对边平行且相等的四边形是平行四边形:①③或②④.共有4种选法.故选B.
9.3 [解析] ∵AC平分∠BAD,∴∠1=∠BAC.
又∵∠1=∠2,∴∠2=∠BAC,∴AB∥DC.
又∵AB=DC,
∴四边形ABCD是平行四边形,∴BC=AD.
又∵∠1=∠2,∴AD=DC=3,∴BC=3.
10.证明:(1)∵BE=CF,
∴BE+EC=CF+EC,即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS).
(2)由(1)得△ABC≌△DEF,
∴∠B=∠DEF,∴AB∥DE.
又∵AB=DE,
∴四边形ABED是平行四边形.
11.证明:(1)∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°.
在△ABE和△CDF中,
∴△ABE≌△CDF(SAS).
(2)∵△ABE≌△CDF,
∴AB=CD,∠ABE=∠CDF,
∴AB∥CD,∴四边形ABCD是平行四边形.
12.证明:(1)∵△ABE,△BCD都是等边三角形,
∴EB=AB,BD=BC,∠EBA=∠DBC=60°,
∴∠EBA-∠DBA=∠DBC-∠DBA,
即∠EBD=∠ABC.
在△EBD和△ABC中,
∴△EBD≌△ABC(SAS).
(2)由(1)知△EBD≌△ABC,∴DE=CA.
∵△ACF是等边三角形,
∴CA=AF,
∴DE=AF.
同理可得EA=DF,
∴四边形DEAF是平行四边形.
13.解:(1)设运动t秒时,四边形ABQP是平行四边形.
根据题意,得AP=t厘米,CQ=2t厘米,
则BQ=(6-2t)厘米.
∵AD∥BC,
∴当AP=BQ时,四边形ABQP是平行四边形,
∴令t=6-2t,解得t=2,
即运动2秒时,四边形ABQP为平行四边形.
(2)由(1),知运动2秒时,四边形ABQP是平行四边形.
设运动x秒时,直线PQ将四边形ABCD截出另一个平行四边形DCQP.
根据题意,得AP=x厘米,CQ=2x厘米,
则PD=(9-x)厘米.
∵AD∥BC,
∴当CQ=PD时,四边形DCQP是平行四边形,
∴令2x=9-x,解得x=3.
因此,运动2秒或3秒时,直线PQ将四边形ABCD截出一个平行四边形.
知识点 1 一组对边平行且相等的四边形是平行四边形
1.在四边形ABCD中,AB∥CD,AB=CD,则四边形ABCD为__________四边形,理由是____________________________________________________________________________.
2.下列不能判定四边形ABCD是平行四边形的是( )
A.AB∥CD,AD∥BC
B.CD∥AB,CD=AB
C.BC∥AD,AB=CD
D.AD∥BC,AD=BC
3.如图,在四边形ABCD中,AD=BC,∠ACB=∠CAD.求证:AB=CD.
4.[2020岳阳]如图,点E,F分别在 ABCD的边BC,AD上,BE=BC,FD=
AD,连接BF,DE.求证:四边形BEDF是平行四边形.
知识点 2 两组对边分别相等的四边形是平行四边形
5.在四边形ABCD中,AB=7 cm,BC=5 cm,当CD=________ cm,AD=________cm时,四边形ABCD是平行四边形.
6.如图,在四边形ABCD中,AB=DC,BC=AD.若∠C=120°,则∠A=________°.
7.如图,在 ABCD中,E,F,G,H分别是AB,BC,CD,DA边上的点,
AE=CG,DH=BF,连接EF,FG,GH,HE.
求证:四边形EFGH是平行四边形.
8.在四边形ABCD中:①AB∥CD;②AD∥BC;③AB=CD;④AD=BC.从中任选两个条件使四边形ABCD为平行四边形的选法共有( )
A.3种 B.4种 C.5种 D.6种
9.如图,已知AC平分∠BAD,∠1=∠2,AB=DC=3,则BC=________.
10.2020北海如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.
(1)求证:△ABC≌△DEF;
(2)连接AD,求证:四边形ABED是平行四边形.
11.如图所示,在四边形ABCD中,AE⊥BD于点E,CF⊥BD于点F,AE=CF,BE=DF.
求证:(1)△ABE≌△CDF;
(2)四边形ABCD是平行四边形.
12.如图,已知△ABC(∠BAC≠60°),分别以△ABC的三边为边在△ABC的同侧作三个等边三角形:△ABE,△BCD,△ACF,连接ED,DF.
求证:(1)△EBD≌△ABC;
(2)四边形DEAF是平行四边形.
13.如图所示,在四边形ABCD中,AD∥BC,BC=6厘米,AD=9厘米,点P,Q分别从点A,C同时出发,点P以1厘米/秒的速度由点A向终点D运动,点Q以2厘米/秒的速度由点C向终点B运动,当一点到达终点时,两点同时停止运动.
(1)运动几秒时,四边形ABQP为平行四边形?
(2)运动几秒时,直线PQ将四边形ABCD截出一个平行四边形?
2.2.2 第1课时 平行四边形的判定定理1, 2
1.平行 一组对边平行且相等的四边形是平行四边形
2.C
3.证明:∵∠ACB=∠CAD,
∴AD∥BC.
又∵AD=BC,
∴四边形ABCD是平行四边形,
∴AB=CD.
4.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC.
∵BE=BC,FD=AD,∴BE=FD.
又∵BE∥FD,∴四边形BEDF是平行四边形.
5.7 5 [解析] 根据两组对边分别相等的四边形是平行四边形可得答案.
6.120
7.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,∠A=∠C,∠B=∠D.
∵AE=CG,DH=BF,
∴AD-DH=BC-BF,AB-AE=CD-CG,
即AH=CF,BE=DG.
在△AEH和△CGF中,
∴△AEH≌△CGF(SAS),∴EH=GF.
在△EBF和△GDH中,
∴△EBF≌△GDH(SAS),
∴EF=GH,
∴四边形EFGH是平行四边形.
8.B [解析] 平行四边形的定义:两组对边分别平行的四边形是平行四边形:①②;平行四边形的判定定理2:两组对边分别相等的四边形是平行四边形:③④;平行四边形的判定定理1:一组对边平行且相等的四边形是平行四边形:①③或②④.共有4种选法.故选B.
9.3 [解析] ∵AC平分∠BAD,∴∠1=∠BAC.
又∵∠1=∠2,∴∠2=∠BAC,∴AB∥DC.
又∵AB=DC,
∴四边形ABCD是平行四边形,∴BC=AD.
又∵∠1=∠2,∴AD=DC=3,∴BC=3.
10.证明:(1)∵BE=CF,
∴BE+EC=CF+EC,即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS).
(2)由(1)得△ABC≌△DEF,
∴∠B=∠DEF,∴AB∥DE.
又∵AB=DE,
∴四边形ABED是平行四边形.
11.证明:(1)∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°.
在△ABE和△CDF中,
∴△ABE≌△CDF(SAS).
(2)∵△ABE≌△CDF,
∴AB=CD,∠ABE=∠CDF,
∴AB∥CD,∴四边形ABCD是平行四边形.
12.证明:(1)∵△ABE,△BCD都是等边三角形,
∴EB=AB,BD=BC,∠EBA=∠DBC=60°,
∴∠EBA-∠DBA=∠DBC-∠DBA,
即∠EBD=∠ABC.
在△EBD和△ABC中,
∴△EBD≌△ABC(SAS).
(2)由(1)知△EBD≌△ABC,∴DE=CA.
∵△ACF是等边三角形,
∴CA=AF,
∴DE=AF.
同理可得EA=DF,
∴四边形DEAF是平行四边形.
13.解:(1)设运动t秒时,四边形ABQP是平行四边形.
根据题意,得AP=t厘米,CQ=2t厘米,
则BQ=(6-2t)厘米.
∵AD∥BC,
∴当AP=BQ时,四边形ABQP是平行四边形,
∴令t=6-2t,解得t=2,
即运动2秒时,四边形ABQP为平行四边形.
(2)由(1),知运动2秒时,四边形ABQP是平行四边形.
设运动x秒时,直线PQ将四边形ABCD截出另一个平行四边形DCQP.
根据题意,得AP=x厘米,CQ=2x厘米,
则PD=(9-x)厘米.
∵AD∥BC,
∴当CQ=PD时,四边形DCQP是平行四边形,
∴令2x=9-x,解得x=3.
因此,运动2秒或3秒时,直线PQ将四边形ABCD截出一个平行四边形.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
