湘教版数学八年级下册 2.5.1 矩形的性质 同步课时作业(word版含答案)
文档属性
| 名称 | 湘教版数学八年级下册 2.5.1 矩形的性质 同步课时作业(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 314.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 00:00:00 | ||
图片预览



文档简介
2.5.1 矩形的性质
知识点 1 矩形的定义
1.已知四边形ABCD是平行四边形,根据矩形的定义,添加一个条件:____________,可使它成为矩形.
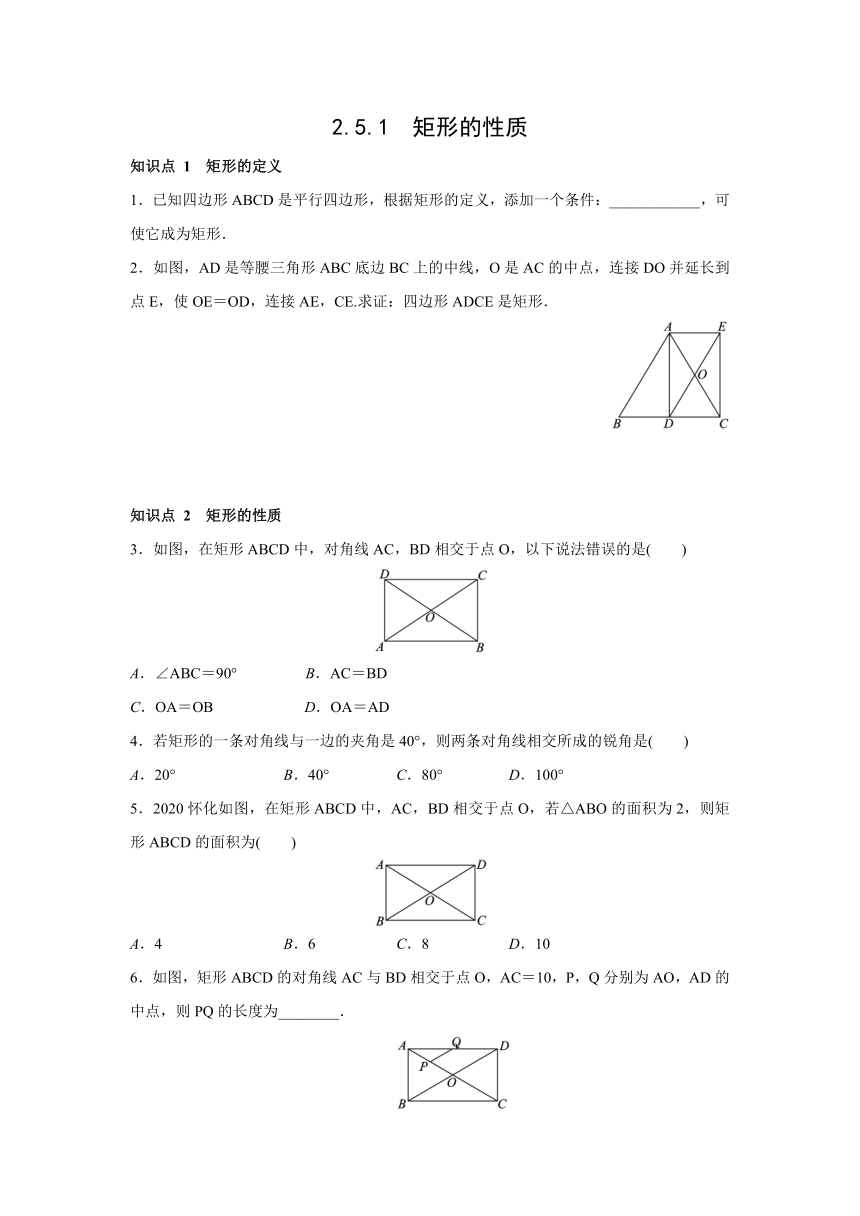
2.如图,AD是等腰三角形ABC底边BC上的中线,O是AC的中点,连接DO并延长到点E,使OE=OD,连接AE,CE.求证:四边形ADCE是矩形.
知识点 2 矩形的性质
3.如图,在矩形ABCD中,对角线AC,BD相交于点O,以下说法错误的是( )
A.∠ABC=90° B.AC=BD
C.OA=OB D.OA=AD
4.若矩形的一条对角线与一边的夹角是40°,则两条对角线相交所成的锐角是( )
A.20° B.40° C.80° D.100°
5.2020怀化如图,在矩形ABCD中,AC,BD相交于点O,若△ABO的面积为2,则矩形ABCD的面积为( )
A.4 B.6 C.8 D.10
6.如图,矩形ABCD的对角线AC与BD相交于点O,AC=10,P,Q分别为AO,AD的中点,则PQ的长度为________.
7.如图,在矩形ABCD中,E是AB的中点,连接DE,CE.
(1)求证:△ADE≌△BCE;
(2)若AB=6,AD=4,求△CDE的周长.
8.如图,E是矩形ABCD的边DC上一点,AB=AE=4,BC=2,则∠EBC的度数为( )
A.10° B.25° C.15° D.20°
9.如图,P是矩形ABCD的边AD上一动点,矩形的两条边AB,BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是( )
A.4.8 B.5 C.6 D.7.2
10.如图,在矩形ABCD中,AB=3,对角线AC,BD相交于点O,AE垂直平分OB,且交OB于点E,则AD的长为________.
11.如图,在矩形ABCD中,点E在BC边上,AE=AD,DF⊥AE,垂足为F.
(1)求证:DF=AB;
(2)若∠FDC=30°,且AB=4,求AD的长.
12.如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若AB=6,∠COD=60°,求矩形ABCD的面积S.
13.如图,在矩形ABCD中,AB=12 cm,BC=6 cm,点P沿AB边从点A开始以2 cm/s的速度向点B移动,点Q沿DA边从点D开始以1 cm/s的速度向点A移动.如果P,Q两点同时出发,用t(s)表示移动时间(0≤t≤6).
(1)直接写出AQ,PB的长(用含t的式子表示);
(2)当t为何值时,△APQ是等腰直角三角形?
(3)求四边形APCQ的面积,并写出一个与计算结果有关的结论.
2.5.1 矩形的性质
1.答案不唯一,如∠A=90° [解析] 有一个角是直角的平行四边形叫矩形.
2.证明:∵O是AC的中点,∴AO=OC.
又∵OE=OD,∴四边形ADCE是平行四边形.
∵AD是等腰三角形ABC底边BC上的中线,
∴AD⊥BC,∴∠ADC=90°,
∴四边形ADCE是矩形.
3.D [解析] ∵四边形ABCD是矩形,
∴∠ABC=90°,AC=BD,OA=AC,OB=BD,
∴OA=OB,∴选项A,B,C正确.故选D.
4.C
5.C [解析] ∵四边形ABCD是矩形,对角线AC,BD相交于点O,∴AC=BD,且OA=OB=OC=OD,∴S△ADO=S△BCO=S△CDO=S△ABO=2,∴矩形ABCD的面积为4S△ABO=8.
故选C.
6.2.5 [解析] ∵四边形ABCD是矩形,
∴AC=BD=10,BO=DO=BD,
∴DO=BD=5.
∵P,Q分别是AO,AD的中点,
∴PQ是△AOD的中位线,
∴PQ=DO=2.5.
故答案为2.5.
7.[解析] (1)由全等三角形的判定定理SAS证得结论;
(2)由(1)中全等三角形的对应边相等和勾股定理求得线段DE的长度,结合三角形的周长公式解答.
解:(1)证明:在矩形ABCD中,AD=BC,
∠A=∠B=90°.
∵E是AB的中点,∴AE=BE.
在△ADE和△BCE中,∴△ADE≌△BCE(SAS).
(2)由(1),知△ADE≌△BCE,
∴DE=CE.
在Rt△ADE中,AD=4,AE=AB=3,
由勾股定理,得DE===5.
又∵AB=CD=6,
∴△CDE的周长为2DE+CD=2×5+6=16.
8.C [解析] ∵四边形ABCD是矩形,∴AD=BC=2,∠D=∠ABC=90°.∵AB=AE=4,
∴AD=AE,∴∠DEA=30°,∴∠EAB=30°.∵AE=AB,∴∠AEB=∠ABE=75°,
∴∠EBC=90°-75°=15°.
9.A [解析] 如图,连接OP,过点P分别作PE⊥OA于点E,PF⊥OD于点F.
∵矩形的两条边AB,BC的长分别为6和8,
∴S矩形ABCD=AB·BC=48,OA=OC,OB=OD,AC=BD=10,
∴OA=OD=5,
∴S△ACD=S矩形ABCD=24,
∴S△AOD=S△ACD=12.
∵S△AOD=S△AOP+S△DOP=OA·PE+OD·PF=×5PE+×5PF=×5(PE+PF)=12,
∴PE+PF=4.8.故选A.
10.3
11.解:(1)证明:在矩形ABCD中,AD∥BC,∠B=90°,
∴∠DAF=∠AEB.
∵DF⊥AE,∴∠DFA=90°,∴∠DFA=∠B.
又∵AD=EA,∴△ADF≌△EAB,∴DF=AB.
(2)∵∠ADF+∠FDC=90°,∠DAF+∠ADF=90°,
∴∠FDC=∠DAF=30°,
∴在Rt△ADF中,AD=2DF.
由(1)知DF=AB,∴AD=2AB=8.
12.解:(1)证明:∵四边形ABCD是矩形,
∴OA=OC,OB=OD.
∵BE=DF,
∴OB-BE=OD-DF,即OE=OF.
在△AOE和△COF中,
∴△AOE≌△COF(SAS),
∴AE=CF.
(2)∵四边形ABCD是矩形,
∴AC=BD,
∴OA=OB=OC=OD.
∵∠AOB=∠COD=60°,
∴△AOB是等边三角形,
由平行四边形的性质可知S矩形ABCD=4S△AOB=4××62=36 .
13.解:(1)AQ=(6-t)cm,PB=(12-2t)cm.
(2)若△APQ为等腰直角三角形,则AQ=AP.
根据题意,知AQ=(6-t)cm,AP=2t cm,
则6-t=2t,解得t=2.
故当t=2时,△APQ是等腰直角三角形.
(3)四边形APCQ的面积=矩形ABCD的面积-三角形CDQ的面积-三角形PBC的面积,即四边形APCQ的面积=6×12-t·12-×6×(12-2t)=72-36=36(cm2).
可得结论:在点P,Q移动过程中,四边形APCQ的面积始终是矩形ABCD面积的一半.
知识点 1 矩形的定义
1.已知四边形ABCD是平行四边形,根据矩形的定义,添加一个条件:____________,可使它成为矩形.
2.如图,AD是等腰三角形ABC底边BC上的中线,O是AC的中点,连接DO并延长到点E,使OE=OD,连接AE,CE.求证:四边形ADCE是矩形.
知识点 2 矩形的性质
3.如图,在矩形ABCD中,对角线AC,BD相交于点O,以下说法错误的是( )
A.∠ABC=90° B.AC=BD
C.OA=OB D.OA=AD
4.若矩形的一条对角线与一边的夹角是40°,则两条对角线相交所成的锐角是( )
A.20° B.40° C.80° D.100°
5.2020怀化如图,在矩形ABCD中,AC,BD相交于点O,若△ABO的面积为2,则矩形ABCD的面积为( )
A.4 B.6 C.8 D.10
6.如图,矩形ABCD的对角线AC与BD相交于点O,AC=10,P,Q分别为AO,AD的中点,则PQ的长度为________.
7.如图,在矩形ABCD中,E是AB的中点,连接DE,CE.
(1)求证:△ADE≌△BCE;
(2)若AB=6,AD=4,求△CDE的周长.
8.如图,E是矩形ABCD的边DC上一点,AB=AE=4,BC=2,则∠EBC的度数为( )
A.10° B.25° C.15° D.20°
9.如图,P是矩形ABCD的边AD上一动点,矩形的两条边AB,BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是( )
A.4.8 B.5 C.6 D.7.2
10.如图,在矩形ABCD中,AB=3,对角线AC,BD相交于点O,AE垂直平分OB,且交OB于点E,则AD的长为________.
11.如图,在矩形ABCD中,点E在BC边上,AE=AD,DF⊥AE,垂足为F.
(1)求证:DF=AB;
(2)若∠FDC=30°,且AB=4,求AD的长.
12.如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若AB=6,∠COD=60°,求矩形ABCD的面积S.
13.如图,在矩形ABCD中,AB=12 cm,BC=6 cm,点P沿AB边从点A开始以2 cm/s的速度向点B移动,点Q沿DA边从点D开始以1 cm/s的速度向点A移动.如果P,Q两点同时出发,用t(s)表示移动时间(0≤t≤6).
(1)直接写出AQ,PB的长(用含t的式子表示);
(2)当t为何值时,△APQ是等腰直角三角形?
(3)求四边形APCQ的面积,并写出一个与计算结果有关的结论.
2.5.1 矩形的性质
1.答案不唯一,如∠A=90° [解析] 有一个角是直角的平行四边形叫矩形.
2.证明:∵O是AC的中点,∴AO=OC.
又∵OE=OD,∴四边形ADCE是平行四边形.
∵AD是等腰三角形ABC底边BC上的中线,
∴AD⊥BC,∴∠ADC=90°,
∴四边形ADCE是矩形.
3.D [解析] ∵四边形ABCD是矩形,
∴∠ABC=90°,AC=BD,OA=AC,OB=BD,
∴OA=OB,∴选项A,B,C正确.故选D.
4.C
5.C [解析] ∵四边形ABCD是矩形,对角线AC,BD相交于点O,∴AC=BD,且OA=OB=OC=OD,∴S△ADO=S△BCO=S△CDO=S△ABO=2,∴矩形ABCD的面积为4S△ABO=8.
故选C.
6.2.5 [解析] ∵四边形ABCD是矩形,
∴AC=BD=10,BO=DO=BD,
∴DO=BD=5.
∵P,Q分别是AO,AD的中点,
∴PQ是△AOD的中位线,
∴PQ=DO=2.5.
故答案为2.5.
7.[解析] (1)由全等三角形的判定定理SAS证得结论;
(2)由(1)中全等三角形的对应边相等和勾股定理求得线段DE的长度,结合三角形的周长公式解答.
解:(1)证明:在矩形ABCD中,AD=BC,
∠A=∠B=90°.
∵E是AB的中点,∴AE=BE.
在△ADE和△BCE中,∴△ADE≌△BCE(SAS).
(2)由(1),知△ADE≌△BCE,
∴DE=CE.
在Rt△ADE中,AD=4,AE=AB=3,
由勾股定理,得DE===5.
又∵AB=CD=6,
∴△CDE的周长为2DE+CD=2×5+6=16.
8.C [解析] ∵四边形ABCD是矩形,∴AD=BC=2,∠D=∠ABC=90°.∵AB=AE=4,
∴AD=AE,∴∠DEA=30°,∴∠EAB=30°.∵AE=AB,∴∠AEB=∠ABE=75°,
∴∠EBC=90°-75°=15°.
9.A [解析] 如图,连接OP,过点P分别作PE⊥OA于点E,PF⊥OD于点F.
∵矩形的两条边AB,BC的长分别为6和8,
∴S矩形ABCD=AB·BC=48,OA=OC,OB=OD,AC=BD=10,
∴OA=OD=5,
∴S△ACD=S矩形ABCD=24,
∴S△AOD=S△ACD=12.
∵S△AOD=S△AOP+S△DOP=OA·PE+OD·PF=×5PE+×5PF=×5(PE+PF)=12,
∴PE+PF=4.8.故选A.
10.3
11.解:(1)证明:在矩形ABCD中,AD∥BC,∠B=90°,
∴∠DAF=∠AEB.
∵DF⊥AE,∴∠DFA=90°,∴∠DFA=∠B.
又∵AD=EA,∴△ADF≌△EAB,∴DF=AB.
(2)∵∠ADF+∠FDC=90°,∠DAF+∠ADF=90°,
∴∠FDC=∠DAF=30°,
∴在Rt△ADF中,AD=2DF.
由(1)知DF=AB,∴AD=2AB=8.
12.解:(1)证明:∵四边形ABCD是矩形,
∴OA=OC,OB=OD.
∵BE=DF,
∴OB-BE=OD-DF,即OE=OF.
在△AOE和△COF中,
∴△AOE≌△COF(SAS),
∴AE=CF.
(2)∵四边形ABCD是矩形,
∴AC=BD,
∴OA=OB=OC=OD.
∵∠AOB=∠COD=60°,
∴△AOB是等边三角形,
由平行四边形的性质可知S矩形ABCD=4S△AOB=4××62=36 .
13.解:(1)AQ=(6-t)cm,PB=(12-2t)cm.
(2)若△APQ为等腰直角三角形,则AQ=AP.
根据题意,知AQ=(6-t)cm,AP=2t cm,
则6-t=2t,解得t=2.
故当t=2时,△APQ是等腰直角三角形.
(3)四边形APCQ的面积=矩形ABCD的面积-三角形CDQ的面积-三角形PBC的面积,即四边形APCQ的面积=6×12-t·12-×6×(12-2t)=72-36=36(cm2).
可得结论:在点P,Q移动过程中,四边形APCQ的面积始终是矩形ABCD面积的一半.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
