湘教版数学八年级下册同步课时作业 2.6.1 菱形的性质(word版、含答案)
文档属性
| 名称 | 湘教版数学八年级下册同步课时作业 2.6.1 菱形的性质(word版、含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 304.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 00:00:00 | ||
图片预览

文档简介
2.6.1 菱形的性质
知识点 1 菱形的定义
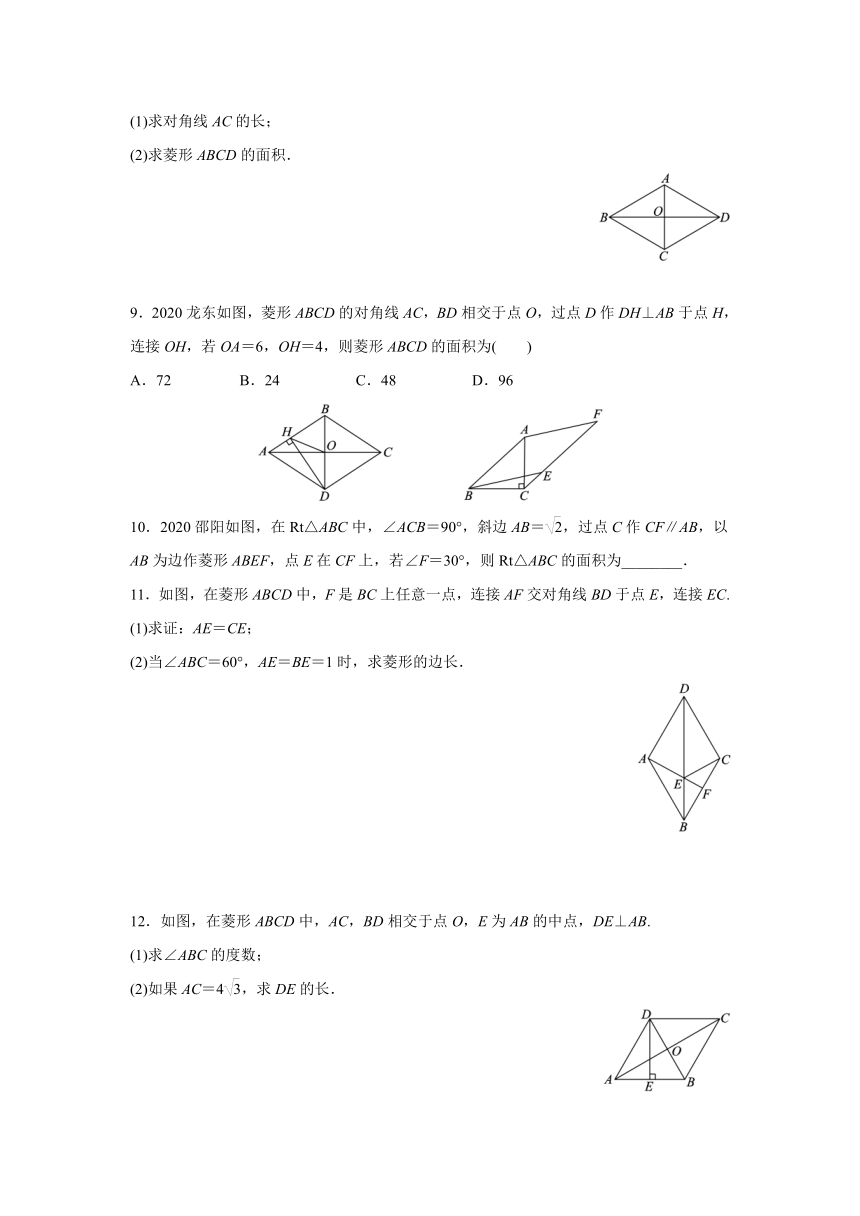
1.如图,在四边形ABCD中,AB=CD,AD=BC,若利用菱形的定义判定四边形ABCD是菱形,则应添加的一个条件是___________________________________(填一个即可).
知识点 2 菱形的性质
2.下列性质中菱形不一定具有的是( )
A.对角线互相平分 B.对角线互相垂直
C.对角线相等 D.既是轴对称图形又是中心对称图形
3.如图,已知菱形ABCD的边长等于2,∠DAB=60°,则对角线BD的长为( )
A.1 B. C.2 D.2
4.如图,在菱形ABCD中,对角线AC,BD相交于点O,若AB=5,AC=6,则BD的长是( )
A.8 B.7 C.4 D.3
5.如图,在菱形ABCD中,过点B作BE⊥AD于点E,过点B作BF⊥CD于点F.
求证:AE=CF.
知识点 3 菱形面积的计算
6.已知菱形的边长和一条对角线的长均为2 cm,则菱形的面积为( )
A.3 cm2 B.4 cm2 C. cm2 D.2 cm2
7.已知一个菱形的两条对角线的长分别为6 cm和8 cm,则这个菱形的面积为________cm2.
8.如图,菱形ABCD的边长为4,∠BAD=120°,对角线AC,BD相交于点O.
(1)求对角线AC的长;
(2)求菱形ABCD的面积.
9.2020龙东如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=6,OH=4,则菱形ABCD的面积为( )
A.72 B.24 C.48 D.96
10.2020邵阳如图,在Rt△ABC中,∠ACB=90°,斜边AB=,过点C作CF∥AB,以AB为边作菱形ABEF,点E在CF上,若∠F=30°,则Rt△ABC的面积为________.
11.如图,在菱形ABCD中,F是BC上任意一点,连接AF交对角线BD于点E,连接EC.
(1)求证:AE=CE;
(2)当∠ABC=60°,AE=BE=1时,求菱形的边长.
12.如图,在菱形ABCD中,AC,BD相交于点O,E为AB的中点,DE⊥AB.
(1)求∠ABC的度数;
(2)如果AC=4,求DE的长.
13.如图,在菱形ABCD中,∠B=60°,AB=4,等边三角形AEF绕点A旋转,AE与BC边相交于点M,AF与CD边相交于点N,连接MN.
(1)求证:∠DAN=∠CAM;
(2)求四边形AMCN的面积;
(3)当∠BAM的度数为多少时,MN的值最小?
2.6.1 菱形的性质
1.答案不唯一,如AB=BC
2.C
3.C
4.A [解析] ∵四边形ABCD是菱形,∴OA=OC=3,OB=OD,AC⊥BD.
在Rt△AOB中,根据勾股定理,得OB===4,
∴BD=2OB=8.故选A.
5.证明:∵四边形ABCD为菱形,
∴BA=BC,∠A=∠C.
∵BE⊥AD,BF⊥CD,
∴∠BEA=∠BFC=90°.
在△ABE和△CBF中,
∴△ABE≌△CBF(AAS),
∴AE=CF.
6.D
7.24 [解析] 菱形的面积=×6×8=24(cm2).
8.解:(1)在菱形ABCD中,AB=BC,∠BAO=∠BAD=×120°=60°,
∴△ABC为等边三角形,
∴AC=AB=4.
(2)由题意,知在菱形ABCD中,AC⊥BD,AC=4,
∴△AOB为直角三角形,AO=AC=2,
∴OB2=AB2-AO2=42-22=12,
∴OB=2 ,∴BD=2OB=4 ,
故S菱形ABCD=AC·BD=×4×4 =8 .
9.C [解析] ∵四边形ABCD是菱形,∴OA=OC,OB=OD,AC⊥BD.
∵DH⊥AB,∴∠BHD=90°,∴BD=2OH.∵OH=4,∴BD=8.
∵OA=6,∴AC=12,∴菱形ABCD的面积为AC·BD=×12×8=48.故选C.
10. [解析] 如图,分别过点E,C作EH⊥AB,CG⊥AB,垂足分别为H,G.∵四边形ABEF为菱形,∴AB=BE=,∠ABE=∠F=30°,∴在Rt△BHE中,EH=.∵AB∥CF,
∴CG=EH=,∴Rt△ABC的面积为××=.
11.解:(1)证明:在菱形ABCD中,AB=CB,∠ABE=∠CBE.
又∵BE=BE,∴△ABE≌△CBE(SAS),
∴AE=CE.
(2)在菱形ABCD中,
∠ABE=∠CBE=∠ABC=×60°=30°.
∵AE=BE=1,
∴∠EAB=∠EBA=30°,
∴∠AED=60°.
∵AD∥BC,∴∠ADE=∠CBE=30°,
∴∠DAE=90°,
∴DE=2AE=2,AD==.
∴菱形的边长是.
12.解:(1)∵E为AB的中点,DE⊥AB,
∴AD=DB.
∵四边形ABCD是菱形,
∴AB=AD,AD∥BC,
∴AD=DB=AB,
∴△ABD为等边三角形,
∴∠DAB=60°.
∵AD∥BC,
∴∠ABC=180°-∠DAB=180°-60°=120°.
(2)∵四边形ABCD是菱形,
∴BD⊥AC,AO=AC=×4 =2.
由题意及(1)可知DE和AO都是等边三角形ABD的高,∴DE=AO=2.
13.解:(1)证明:∵在菱形ABCD中,∠B=60°,
∴△ABC,△ACD都是等边三角形.
∵△AEF是等边三角形,
∴∠DAN+∠FAC=∠CAM+∠FAC=60°,
∴∠DAN=∠CAM.
(2)由题意及(1),得∠CAM=∠DAN,AC=AD,∠ACM=∠ADN,
∴△ACM≌△ADN,
∴S△ACD=S△ACN+S△ADN=S△ACN+S△ACM=S四边形AMCN.
由△ACD为等边三角形,且AD=AB=4,
可求得S△ACD=4 .
∴S四边形AMCN=4 .
(3)由(2)得△ACM≌△ADN,
∴AM=AN.
又∵∠MAN=60°,
∴△AMN是等边三角形,∴MN=AM.
当AM⊥BC时,AM的值最小,
即MN的值最小,此时AM平分∠BAC,
∴∠BAM=30°,
即当∠BAM=30°时,MN的值最小.
知识点 1 菱形的定义
1.如图,在四边形ABCD中,AB=CD,AD=BC,若利用菱形的定义判定四边形ABCD是菱形,则应添加的一个条件是___________________________________(填一个即可).
知识点 2 菱形的性质
2.下列性质中菱形不一定具有的是( )
A.对角线互相平分 B.对角线互相垂直
C.对角线相等 D.既是轴对称图形又是中心对称图形
3.如图,已知菱形ABCD的边长等于2,∠DAB=60°,则对角线BD的长为( )
A.1 B. C.2 D.2
4.如图,在菱形ABCD中,对角线AC,BD相交于点O,若AB=5,AC=6,则BD的长是( )
A.8 B.7 C.4 D.3
5.如图,在菱形ABCD中,过点B作BE⊥AD于点E,过点B作BF⊥CD于点F.
求证:AE=CF.
知识点 3 菱形面积的计算
6.已知菱形的边长和一条对角线的长均为2 cm,则菱形的面积为( )
A.3 cm2 B.4 cm2 C. cm2 D.2 cm2
7.已知一个菱形的两条对角线的长分别为6 cm和8 cm,则这个菱形的面积为________cm2.
8.如图,菱形ABCD的边长为4,∠BAD=120°,对角线AC,BD相交于点O.
(1)求对角线AC的长;
(2)求菱形ABCD的面积.
9.2020龙东如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=6,OH=4,则菱形ABCD的面积为( )
A.72 B.24 C.48 D.96
10.2020邵阳如图,在Rt△ABC中,∠ACB=90°,斜边AB=,过点C作CF∥AB,以AB为边作菱形ABEF,点E在CF上,若∠F=30°,则Rt△ABC的面积为________.
11.如图,在菱形ABCD中,F是BC上任意一点,连接AF交对角线BD于点E,连接EC.
(1)求证:AE=CE;
(2)当∠ABC=60°,AE=BE=1时,求菱形的边长.
12.如图,在菱形ABCD中,AC,BD相交于点O,E为AB的中点,DE⊥AB.
(1)求∠ABC的度数;
(2)如果AC=4,求DE的长.
13.如图,在菱形ABCD中,∠B=60°,AB=4,等边三角形AEF绕点A旋转,AE与BC边相交于点M,AF与CD边相交于点N,连接MN.
(1)求证:∠DAN=∠CAM;
(2)求四边形AMCN的面积;
(3)当∠BAM的度数为多少时,MN的值最小?
2.6.1 菱形的性质
1.答案不唯一,如AB=BC
2.C
3.C
4.A [解析] ∵四边形ABCD是菱形,∴OA=OC=3,OB=OD,AC⊥BD.
在Rt△AOB中,根据勾股定理,得OB===4,
∴BD=2OB=8.故选A.
5.证明:∵四边形ABCD为菱形,
∴BA=BC,∠A=∠C.
∵BE⊥AD,BF⊥CD,
∴∠BEA=∠BFC=90°.
在△ABE和△CBF中,
∴△ABE≌△CBF(AAS),
∴AE=CF.
6.D
7.24 [解析] 菱形的面积=×6×8=24(cm2).
8.解:(1)在菱形ABCD中,AB=BC,∠BAO=∠BAD=×120°=60°,
∴△ABC为等边三角形,
∴AC=AB=4.
(2)由题意,知在菱形ABCD中,AC⊥BD,AC=4,
∴△AOB为直角三角形,AO=AC=2,
∴OB2=AB2-AO2=42-22=12,
∴OB=2 ,∴BD=2OB=4 ,
故S菱形ABCD=AC·BD=×4×4 =8 .
9.C [解析] ∵四边形ABCD是菱形,∴OA=OC,OB=OD,AC⊥BD.
∵DH⊥AB,∴∠BHD=90°,∴BD=2OH.∵OH=4,∴BD=8.
∵OA=6,∴AC=12,∴菱形ABCD的面积为AC·BD=×12×8=48.故选C.
10. [解析] 如图,分别过点E,C作EH⊥AB,CG⊥AB,垂足分别为H,G.∵四边形ABEF为菱形,∴AB=BE=,∠ABE=∠F=30°,∴在Rt△BHE中,EH=.∵AB∥CF,
∴CG=EH=,∴Rt△ABC的面积为××=.
11.解:(1)证明:在菱形ABCD中,AB=CB,∠ABE=∠CBE.
又∵BE=BE,∴△ABE≌△CBE(SAS),
∴AE=CE.
(2)在菱形ABCD中,
∠ABE=∠CBE=∠ABC=×60°=30°.
∵AE=BE=1,
∴∠EAB=∠EBA=30°,
∴∠AED=60°.
∵AD∥BC,∴∠ADE=∠CBE=30°,
∴∠DAE=90°,
∴DE=2AE=2,AD==.
∴菱形的边长是.
12.解:(1)∵E为AB的中点,DE⊥AB,
∴AD=DB.
∵四边形ABCD是菱形,
∴AB=AD,AD∥BC,
∴AD=DB=AB,
∴△ABD为等边三角形,
∴∠DAB=60°.
∵AD∥BC,
∴∠ABC=180°-∠DAB=180°-60°=120°.
(2)∵四边形ABCD是菱形,
∴BD⊥AC,AO=AC=×4 =2.
由题意及(1)可知DE和AO都是等边三角形ABD的高,∴DE=AO=2.
13.解:(1)证明:∵在菱形ABCD中,∠B=60°,
∴△ABC,△ACD都是等边三角形.
∵△AEF是等边三角形,
∴∠DAN+∠FAC=∠CAM+∠FAC=60°,
∴∠DAN=∠CAM.
(2)由题意及(1),得∠CAM=∠DAN,AC=AD,∠ACM=∠ADN,
∴△ACM≌△ADN,
∴S△ACD=S△ACN+S△ADN=S△ACN+S△ACM=S四边形AMCN.
由△ACD为等边三角形,且AD=AB=4,
可求得S△ACD=4 .
∴S四边形AMCN=4 .
(3)由(2)得△ACM≌△ADN,
∴AM=AN.
又∵∠MAN=60°,
∴△AMN是等边三角形,∴MN=AM.
当AM⊥BC时,AM的值最小,
即MN的值最小,此时AM平分∠BAC,
∴∠BAM=30°,
即当∠BAM=30°时,MN的值最小.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
